5. Klasse - humboldt

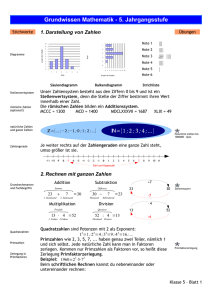
Grundwissen-Mathematik-5.Jahrgangsstufe
•
Zahlenmengen
ℕ = {1,2,3,...}
ℕo = {0,1,2,3,...}
ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Vielfachmengen
Teilermengen
Menge der Quadratzahlen
Menge der Primzahlen
G8
Menge der natürlichen Zahlen
Menge der natürlichen Zahlen mit Null
Menge der ganzen Zahlen
Beispiel: V(3) = {3,6,9,...}; Es gilt: 9∈V(3), 7∉V(3)
Beispiel: T(12) = {1,2,3,4,6,12}
{1,4,9,16,25,...}
{2,3,5,7,11,13,...}
Anwendung: Primfaktorenzerlegung
Beispiel: 72 = 23⋅32
•
Zehnersystem
Zahlen werden mit Hilfe von Ziffern dargestellt
Beispiel: 568 = 5⋅100 + 6⋅10 + 8⋅1
Stufenzahlen des Zehnersystems: 1, 10, 100, 1000, ...
Zehnerpotenzen: 100 = 1, 101 = 10, 102 = 100, 103 = 1000, ...
Beispiel: 87⋅106 = 87 000 000
•
Runden
Es wird so gerundet, dass der Rundungsfehler möglichst klein ist. Ist der Fehler beim
Aufrunden und beim Abrunden gleich, so wird aufgerundet.
Beispiele:
Runde auf Tausender: 16528 ≈ 17000; 14500 ≈ 15000; 19438≈19000
Runde auf Stunden:
37min ≈ 1h
•
Römische Zahlzeichen
I =1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000
•
Ganze Zahlen
Darstellung der ganzen Zahlen auf der Zahlengeraden
x
–3
–2
–1
0
1
2
3
Betrag: Der Betrag einer Zahl ist der Abstand der Zahl von 0
Beispiele:
3 = 3; −3 = 3
Gegenzahl: Zahl und Gegenzahl unterscheiden sich nur durch ihr Vorzeichen
Beispiele:
–3 ist die Gegenzahl von 3
3 ist die Gegenzahl von –3
0 ist die Gegenzahl von 0
Rechnen mit ganzen Zahlen
Beispiele:
3 + 2 = 5;
3 – 2 = 1;
3⋅2 = 6;
3⋅(–2) = –6;
12:2 = 6;
–12:2 = –6;
–3 + 2 = –1;
–3⋅2 = –6;
12:(–2) = –6;
–3 – 2 = –5;
–3⋅(–2) = 6;
–12:(–2) = 6;
1
Grundwissen-Mathematik-5.Jahrgangsstufe
•
G8
Terme
Sinnvolle Rechenausdrücke heißen Terme
Termnamen
Beispiel: 12 + 3 = 15
Der Term 12 + 3 ist eine Summe
1. Summand: 12
2. Summand: 3
Wert der Summe: 15
Beispiel: 12 – 3 = 9
Der Term 12 – 3 ist eine Differenz
Minuend: 12
Subtrahend: 3
Wert der Differenz: 9
Beispiel: 12⋅3 = 36
Der Term 12⋅3 ist ein Produkt
1. Faktor: 12
2. Faktor: 3
Wert des Produkts: 36
Beispiel: 12:3 = 4
Der Term 12:3 ist ein Quotient
Dividend: 12
Divisor: 3
Wert des Quotienten: 4
Beispiel: 34 = 3⋅3⋅3⋅3 =81
Der Term 34 ist eine Potenz
Basis: 3
Exponent: 4
Wert der Potenz: 81
Rechengesetze (a, b, c ∈ ℤ)
Kommutativgesetze:
Beispiele:
a+b=b+a
2+3=3+2
a⋅b=b⋅a
2⋅3=3⋅2
Assoziativgesetze:
Beispiele:
a + (b + c) = (a + b) + c
2 + (3 + 4) = (2 + 3) + 4
a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c
2 ⋅ (3 ⋅ 4) = (2 ⋅ 3) ⋅ 4
Distributivgesetze:
Beispiele:
a⋅(b + c) = a⋅b + a⋅c
2⋅(3 + 4) = 2⋅3 + 2⋅4
a ⋅ (b – c) = a ⋅ b – a ⋅ c
2 ⋅ (3 – 4) = 2 ⋅ 3 – 2 ⋅ 4
Rechenregeln: Klammern zuerst, dann Potenzen, dann Punktrechnungen, dann
Strichrechnungen. Sind nur Punktrechnungen oder nur Strichrechnungen vorhanden, wird
von links nach rechts gerechnet.
Beispiele:
(2 ⋅ 34 – 5 ⋅ 3) : 7 – 5 = (2 ⋅ 81 – 15) : 7 – 5 = (162 – 15) : 7 – 5 = 147 : 7 – 5 = 21 – 5 = 16
180 : 9 ⋅ 6 : 2 ⋅ 5 = 20 ⋅ 6 : 2 ⋅ 5 = 120 : 2 ⋅ 5 = 60 ⋅ 5 = 300
•
Größen
Eine Größe besteht aus einer Maßzahl und einer Einheit
Beispiel: 25km ist eine Größe. Die Maßzahl ist 25, die Einheit ist km.
2
Grundwissen-Mathematik-5.Jahrgangsstufe
•
Rechnen mit Größen
Einheiten und Umrechnungen
Währung: 1€ = 100ct
Längen: 1m = 10dm = ...
Massen: 1t = 1000kg = ...
Flächen: 1m² = 100dm² = ...
Zeit:
1d = 24h = ...
Beispiele:
5m 3cm – 2m 8dm = 503cm – 280cm = 223cm = 2,23m
35ha 70a + 80ha 47a = 115ha 117a = 116ha 17a = 1km² 16ha 17a
7 ⋅ 5,25kg = 7 ⋅ 5250g = 36750g = 36,75kg
•
Maßstab
Beispiel: Der Maßstab beträgt
Wirklichkeit.
•
d.h. 1cm auf der Karte sind 1km in
Geometrische Grundfiguren
Rechteck, Quadrat, Parallelogramm, Raute, Trapez, Kreis
Umfang des Rechtecks:
Flächeninhalt des Rechtecks:
•
1:100000,
G8
u = 2⋅(ℓ + b)
A = ℓ⋅b
(ℓ = Länge, b = Breite)
Geometrische Grundkörper
Quader, Würfel, Prisma, Pyramide, Zylinder, Kegel, Kugel
Oberflächeninhalt des Quaders: A = 2⋅(ℓ⋅b + ℓ⋅h + b⋅h) (ℓ = Länge, b = Breite, h = Höhe)
Netz des Quaders:
•
Punktmengen
Strecke [AB]
A
B
Die Länge AB der Strecke [AB] ist die Entfernung von A und B.
Gerade AB
Halbgerade oder Strahl [AB
A
B
A
B
3
Grundwissen-Mathematik-5.Jahrgangsstufe
Senkrechte Geraden:
G8
h
g ist ein Lot zu h und umgekehrt.
Schreibweise g ⊥ h:
g
Zwei Geraden g und h der Zeichenebene sind
zueinander parallel, wenn sie ein gemeinsames
Lot in der Zeichenebene besitzen.
Schreibweise: g║h.
g
h
P
Der Abstand d des Punktes P von der Geraden g
ist die Länge der Lotstrecke [PF].
g
F
•
Achsensymmetrie
Figuren, die man durch Falten aufeinander legen kann, heißen achsensymmetrisch. Die
Faltgerade ist die Symmetrieachse. Ist P’ Spiegelpunkt von P, so wird die Strecke [PP’]
von der Symmetrieachse a rechtwinklig halbiert.
P
P'
a
•
Winkel
Dreht man eine Halbgerade um ihren Anfangspunkt S, so entsteht ein Winkel. S ist der
Scheitel des Winkels, [SA und [SB sind die Schenkel des Winkels.
α = ∢(g,h) = ∢ASB
Bezeichnungen:
h
α = 0°:
Nullwinkel
B
0° < α < 90°:
spitzer Winkel
α = 90°:
rechter Winkel
α
S
90° < α <180°:
stumpfer Winkel
α = 180°:
gestreckter Winkel
A
180° < α < 360°: überstumpfer Winkel
g
α = 360°:
Vollwinkel
4
Grundwissen-Mathematik-5.Jahrgangsstufe
•
G8
Das Koordinatensystem
Jeder Punkt in einem Koordinatensystem lässt sich durch Angabe eines Zahlenpaares
beschreiben. Diese Zahlen heißen Koordinaten.
y
Beispiel: P(–2 | 3), Q(3 | –4)
Px
1
x
1
x
Q
Die Zeichenebene wird durch das Koordinatensystem in 4 Quadranten unterteilt:
y
I
II
x
IV
III
•
Diagramme
Der Zusammenhang zwischen Größen kann in Tabellen und Diagrammen dargestellt
werden.
Beispiel:
Klasse
Schüler
5a
28
5b
23
5c
30
5d
25
Säulendiagramm:
35
30
25
20
15
10
5
0
5a
5b
5c
5d
5
Grundwissen-Mathematik-5.Jahrgangsstufe
•
G8
Stochastik
Zählprinzip, Veranschaulichung am Baumdiagramm
Beispiel:
Auf wie viele Arten kann man 3 verschiedene Pullover und 2 verschiedene Hosen
kombinieren?
Es gibt 3⋅2 = 6 Möglichkeiten
Baumdiagramm:
H1
P1
H2
H1
P2
H2
H1
P3
H2
6