O17a

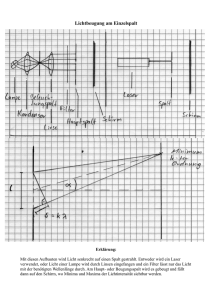
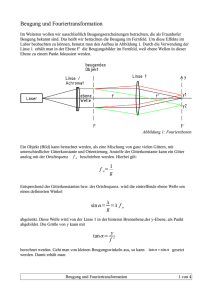
Fakultät für Physik und Geowissenschaften
Physikalisches Grundpraktikum
O 17a
„Beugung (Laserlicht)“
Aufgaben
1. Bestimmen Sie durch Beugung (Fraunhofer, Fresnel) von Laserlicht am Einfachspalt dessen Breite.
Messen Sie hierzu die Intensität des gebeugten Lichts mit einer CCD-Zeilenkamera; bestimmen Sie
die Spaltbreite aus der Lage der Minima verschiedener Ordnungen.
2. Nehmen Sie die Intensitätsverteilung des an einem Doppelspalt gebeugten Laserlichts mit einer
CCD-Zeilenkamera auf. Bestimmen Sie den Mittenabstand der Spalte und die Spaltbreite aus (a) der
Lage der Minima verschiedener Ordnungen sowie durch (b) den Fit des bekannten FraunhoferBeugungsbilds an die Daten.
3. Bestimmen Sie die Gitterkonstante eines Transmissionsgitters durch Ausmessung der Lage der
Maxima.
Literatur
Physikalisches Praktikum, 13. Auflage, Hrsg. W. Schenk, F. Kremer, Optik, 2.0, 2.2, 2.3
Gerthsen Physik, D. Meschede, 22. Auflage, 517-524
Zubehör
Diodenlaser mit Strahlaufweitung (λ = 636 nm), CCD-Zeilenkamera (Thorlabs mit Software), PC,
Drucker, Messschraubenokular, Polarisationsfilter, Einzel- und Doppelspalt, Transmissionsgitter,
Reflexionsgitter, Millimeterskale mit Lochblende
Schwerpunkte zur Vorbereitung
- Interferenz, Kohärenz, Kohärenzbedingung
- Beugung am Spalt, Doppelspalt, Reflexions- und Transmissionsgitter
- Beugung nach Fraunhofer und Fresnel
- Aufbau und Funktionsweise eines Lasers, He-Ne-Laser
- Eigenschaften von Laserlicht, Gesetz von Malus
- Prinzipieller Aufbau eines CCD-Sensors
1
Sicherheitshinweis
Der Laser-Primärstrahl (Laserklasse 2) hat eine Leistung von ca. 1 mW. Direktes Hineinsehen in den
Laser-Primärstrahl kann zu Augenverletzungen führen. Bei der Beobachtung der Interferenz mit
einem Okularmikrometer Ist ein Polarisationsfilter zur Abschwächung der Intensität zwischen Laser
und Spalt einzubringen (Gesetz von Malus).
Fraunhofersche- und Fresnelsche Beugung
Es wird bei Beugungserscheinungen zwischen der Beugung (Beobachtungsart) nach Fraunhofer und
nach Fresnel unterschieden. Bei der Fraunhoferschen Beugung oder Beugung paralleler Strahlen
betrachtet man die Beugung ebener Wellen. Im letztgenannten Fall ist der Abstand zwischen
Lichtquelle und dem Hindernis (z.B. Spalt), an dem die Beugung erfolgt, und der Abstand zwischen
Beobachtungspunkt und Hindernis stets unendlich. Im Experiment erreicht man diese Art von
Beugung, indem man die Lichtquelle in den Brennpunkt einer Sammellinse stellt oder eine
Lichtquelle (Laser) verwendet, die selbst ebene Wellen aussendet. Das Beugungsbild betrachtet man
in der Brennpunktsebene einer Sammellinse auf einem Schirm oder wie in unserem Fall mit einer
CCD-Zeilenkamera.
Als Fresnelsche Beugung wird jene Art von Lichtbeugung bezeichnet, bei deren Berechnung die
Krümmung der Wellenfront der einfallenden sowie der gebeugten Welle nicht vernachlässigt werden
kann, die Strahlen also nicht parallel verlaufen. Fresnelsche Beugung tritt dann auf, wenn sich sowohl
die Lichtquelle als auch die Beobachtungsebene des Beugungsbildes oder auch nur letztere sich in
einem endlichen Abstand zu dem beugenden Hindernis befindet. Die Berechnung dieser Probleme
ist zumeist sehr kompliziert. Für Fresnelsche Beugung am geraden Spalt entscheidet u. a. die Größe
des Wellenparameters w über die Intensitätsverteilung in der Beobachtungsebene
w=
λa
b
.
Dabei sind a der Abstand zwischen Spaltebene und der zu ihr parallelen Beobachtungsebene, b die
Spaltbreite und λ die Wellenlänge des verwendeten monochromatischen Lichts. In analoger Weise
bestimmt bei der Beugung am Doppelspalt (Spaltabstand g) die Fresnel-Zahl NF mit NF =
g2
den
4a λ
Übergang der Beobachtung der Fresnel-Beugung zur Fraunhofer-Beugung für NF < 1.
Abb. 1.1 Schematische Darstellung der Intensitätsverteilung
bei Beugung an einem breiten Spalt (w <<1)
2
Für w ≈ 1 umfassen die Intensitätsschwankungen den gesamten Bereich zwischen x1 und x2. Je nach
dem Wert von w kann in der Mitte des Beugungsbilds ein Maximum oder ein Minimum der Intensität
auftreten. Bei w>>1 (b>λ) aber entspricht das Beugungsbild dem der Fraunhoferschen Beugung. Das
Hauptmaximum der Intensität befindet sich hinter der Spaltmitte und ist umso mehr
"verschwommen", je enger der Spalt ist.
Hinweise zu Aufgabe 1
Die Auswahl des Einfachspaltes (A, B oder C) wird vom Betreuer vorgenommen. Es ist die
Beobachtungsart nach Fraunhofer zu realisieren. Dazu stellt man den Spalt (Abb. 1.2) so auf, dass
seine Ebene senkrecht zur Achse der optischen Bank steht. Das auftreffende Licht passiert die
rechteckige Öffnung des Spaltes zum Teil ungestört in seiner ursprünglichen Richtung und wird zum
anderen Teil gebeugt.
Abb. 1.2 Zur Beugung nach Fraunhofer
Alle die durch den Spalt der Breite b ungestört hindurchtretenden achsenparallelen (nicht
gebeugten) Strahlen werden in der Brennebene F′ der Sammellinse L bei x = 0 gesammelt. Ihr
Gangunterschied ist null, so dass sie sich verstärken. Der Gangunterschied Δ ist definiert als die
Differenz der optischen Weglängen s (Δ = s1-s2 für Luft mit der Brechzahl n = 1) der miteinander
interferierenden Strahlen. Parallelstrahlen, die von einzelnen Punkten des Spaltes unter dem
gleichen Winkel α ausgehen (homologe Punkte), werden bei x = f tanα vereinigt, wobei f die
Brennweite der Sammellinse ist. Zwischen diesen Strahlen treten jedoch Gangunterschiede Δ auf. Ist
z.B. Δ= λ zwischen den beiden Randstrahlen, so löschen sich jeweils ein Strahl der oberen und der
3
unteren Spalthälfte, die von zwei Spaltpunkten mit dem Abstand b/2 ausgehen, bei Vereinigung
durch L gegenseitig aus. Für das Minimum beliebiger Ordnungen1 (n = ±1, ±2,...) gilt dann
b sinα n = n λ .
(1)
Minimale Beleuchtungsstärke (Dunkelheit) tritt in der Brennebene F′ an den Stellen
⎡
⎛ n λ ⎞⎤
xn = f tanα n = f tan ⎢arcsin ⎜
⎟⎥
⎝ b ⎠⎦
⎣
auf. Für kleine Beugungswinkel α erhält man xn ≈ f
(2)
nλ
.
b
Zur Ausmessung des Beugungsbildes wird die CCD-Kamera so auf der optischen Bank positioniert,
dass sich ihre Brennebene FCCD genau im Abstand der gegebenen Brennweite f von L befindet. Dann
erscheint ein besonders scharfes Bild der Minima und Maxima. Anschließend wird mit der CCDKamera die Intensitätsverteilung ausgemessen; die Daten werden abgespeichert und in ORIGIN
importiert. Die Abstände 2xn zwischen den ±n-ten Minima werden in ORIGIN bestimmt. Die
Auswertung erfolgt mittels linearer Regression (xn vs. n).
In Ergänzung zur Fraunhoferschen Beugung ist das Beugungsbild durch Fresnelsche Beugung
auszumessen und die Spaltbreite b zu bestimmen. Dazu ist der Abstand a zwischen Spaltebene und
CCD-Sensor zu messen. Unter Verwendung der Beziehungen
tanα n =
xn
a
und
sinα n = n
λ
b
(3a,b)
kann durch Ausmessen der Lage der Minima wie bereits oben ausgeführt der Wert für b bestimmt
a
werden. Für kleine Winkel gilt wieder die Näherung xn ≈ n λ .
b
Es sind beide Ergebnisse unter Berücksichtigung der unterschiedlichen Beobachtungsverfahren zu
diskutieren.
Hinweise zu Aufgabe 2
Ein Doppelspalt besteht aus zwei parallelen Spalten gleicher Spaltbreite b mit dem Mittenabstand g
zwischen den Spalten. Bei der Berechnung der Beugung nach Fresnel muss wie bereits oben
beschrieben die Krümmung der Wellenfront (I) der einfallenden sowie der gebeugten Welle oder (II)
nur der gebeugten Welle berücksichtigt werden. Bei unserer Versuchsanordnung liegt Fall (II) vor.
Die von zwei Punkten F1 und F2 der Einzelspalte des Doppelspaltes ausgehenden Wellenzüge
besitzen in einem Punkt P des (gebeugten) Wellenfeldes den Gangunterschied Δ= r1 - r2 mit r1 = F1P
1
Für die Betrachtung Minima höherer Ordnungen muss man die Spaltbreite in Viertel (n = ±2), Sechstel
(n = ±3) usw. einteilen.
4
und r2 = F2P (Abb. 2.1). Alle Punkte mit gleichem Gangunterschied Δ (bzw. Phasendifferenz δ = Δ
2π/λ) liegen somit definitionsgemäß auf einem zweischaligen Rotationshyperboloid mit F1 und F2 als
Brennpunkten und der Verbindungslinie F1F2 als Hauptachse (Rotationsachse).
Abb. 2.1
Konfokale Hyperbeln, Brennpunkte im Abstand e
von der Hauptachse, jede Hyperbel gibt Orte
gleichen Gangunterschiedes Δ an.
Die von F1 und F2 ausgehenden Wellen verstärken sich z.B. bei einer Phasendifferenz δ = 2 nπ (n = ±1,
±2,...). Im Versuch werden die Rotationshyperboloide von einem ebenen Schirm (CCD-Zeile) im
Abstand d von der Rotationsachse geschnitten, der senkrecht zur optischen Achse (Hauptachse der
Hyperbeln) steht. In einem genügend kleinen Gebiet um die optische Achse können Maxima und
Minima in gleichgroßen Abständen zueinander beobachtet werden.
In Abb. 2.2 ist die Überlagerung von zwei durch den Doppelspalt gebeugten Teilbündeln dargestellt.
Abb. 2.2 Zur Beugung am Doppelspalt
Im Abstand x1 interferieren diese Teilbündel. Der Gangunterschied Δ zwischen ihnen ergibt sich über
2
⎛g
⎞
r = ⎜ + x1 ⎟ + d 2
⎝2
⎠
2
1
2
⎛g
⎞
r = ⎜ − x1 ⎟ + d 2
⎝2
⎠
2
2
und
mit d >> g, d >> x1 und r1 ≈ r2 ≈ d zu
Δ = r1 − r2 =
r12 − r22 g
≈ x1
r1 + r2 d
.
(4)
5
Ist der Gangunterschied Δ = n λ (n = ±1, ±2,...), so beobachtet man im Abstand
xnmax = n λ
d
g
(5)
Maxima bzw. für Δ = (2n - 1) λ/2 (n = ±1, ±2,...) im Abstand
xnmin = (2 n − 1)
λd
(6)
2 g
Minima. Aus n λ = gxn / d = g tanα n ≈ g sinα n
erkennt man, dass bei großen Abständen d (tanα ≈ sinα ) im Falle der Fresnel-Beugung die Formeln
der Fraunhofer-Beugung verwendet werden können.
Dem Beugungsbild des Doppelspaltes ist das Beugungsbild seiner Einzelspalte überlagert (Abb. 2.3).
Für die zugehörigen Minima (blaue Kurve in Abb. 2.3) gilt die gleiche Beziehung wie für den
Einzelspalt: b sinα n = n λ ; n = ± 1 , ± 2 ,...
I
I0
Abb. 2.3 Zur Intensitätsverteilung nach Beugung
am Doppelspalt (schwarz: Doppelspaltfunktion,
blau: Einzelspaltfunktion mit der gleicher
Spaltbreite)
α
Die Intensitätsverteilung des am Doppelspalt gebeugten Lichtes ist gegeben durch
2
⎛ sin p ⎞
2
I = 4 Imax ⎜
⎟ cos q
p
⎝
⎠
mit
p=
π
b sinα
λ
und
q=
π
g sinα .
λ
(7)
Während der Faktor (sin p/p)2 die Beugung am Einzelspalt der Breite b beschreibt, charakterisiert der
Faktor cos2q den Intensitätsverlauf bei Interferenz zweier punktförmiger kohärenter Lichtquellen im
Abstand g zueinander. Die Spaltbreite b und das Verhältnis (g/b) bestimmen maßgeblich die
Intensitätsverhältnisse im Beugungsbild. Bei ganzzahligem Verhältnis m = g/b kann man im zentralen
Maximum 2m Minima beobachten. Berechnen Sie während der Vorbereitung die theoretische
Intensitätsverteilung eines Doppelspaltes in Abhängigkeit ganzzahliger Verhältnisse b/g = 2, 3 und 5
und bestimmen Sie damit die Anzahl der Maxima und der Minima innerhalb der 'Einhüllenden'.
Bestimmung des Spaltabstandes g
6
Bei kleinen Beugungswinkeln α erhält man für die Lage x der Extrema der Intensitäten des
Doppelspaltes (Maxima und Minima der Funktion cos2q):
xn = d tanα n ≈ d sinα n = n
dλ
.
g
(8)
Maxima: n = 0, ±1, ±2,... Minima: n = ±1/2, ±3/2,...
Misst man die Lage der Maxima und Minima im Bereich des zentralen Maximums und trägt die
entsprechenden Werte über n auf, so kann man aus dem Anstieg der Ausgleichsgeraden den
Spaltabstand g bestimmen.
Abschätzung der Spaltbreite b
Die Spaltbreite b ist aus der Lage der Minima 1. Ordnung der Einhüllenden der Intensitätsverteilung
(blaue Kurve in Abb. 2.3) zu ermitteln.
Bestimmung von g und b mittels Fit der Intensitätsverteilung
Passen Sie die das Beugungsbild, Gl. (7), an die Daten an und bestimmen Sie daraus g und b.
Hinweise zu Aufgabe 3
Das Transmissionsgitter ist zwischen Spalt und Skale zu bringen (Abb.3.1) und zu justieren (optische
Achse senkrecht zur Gitterebene). Um die Messgenauigkeit des Abstandes l zwischen Gitterebene
und einer linearen Messskala (Lineal, Mattglasskala) zu erhöhen, vergrößert man den Abstand
zwischen diesen, bis ein k-tes Maximum (k = ±1, ±2 oder ±3) an den Enden der Skale beobachtet
wird. Für die Auswertung werden Gleichungen verwendet, die in Analogie zum Doppelspalt
hergeleitet werden können.
Abb. 3.1 Zur Messung mit
dem Transmissionsgitter
Es gilt: sinα k = k
λ
g
, tanα k =
xk
, αk Beugungswinkel für das k-te Maximum.
l
⎛ l ⎞
Für die Gitterkonstante g ergibt sich g = k λ 1 + ⎜ ⎟
⎝ xk ⎠
7
2
.
Ergänzende Literatur
Bergmann-Schaefer; Bd. III, 8. Aufl. a) Kap. III, 1. S. 325-335; b) Kap. III, 8. S. 384-394; c) Kap. III, 10. S.
404-422
H. Hänsel, W. Neumann: Physik, Spektrum, 1993, Bd. 2, Kap. 10.1, 10.2
Lipson, Lipson, Tannhäuser, Optik, Springer, 1997
Applet for two-slit diffraction:
http://www.lon-capa.org/~mmp/kap27/Gary-TwoSlit/app.htm
Abb.
5 Spektrale
optischer Sensoren
Empfindlichkeit
(a. Fotodiode, b. CCD-Sensor)
Die Bedienungsanleitung der Thorlabs CCD-Line-Camera kann aus dem Downloadbereich der
Praktikumsseiten heruntergeladen werden.
8