Übung Nummer 6.1
Werbung

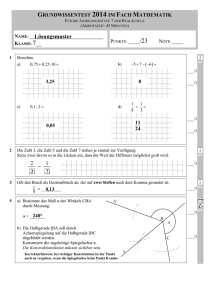
Übung Nummer 6.1 Ein Käfer (m=1g) rotiert windgeschützt auf der Flügelspitze (r=15m) einer Windkraftanlage, die für eine Umdrehung 2 s braucht. Mit welcher Kraft muss sich der Käfer mit seinen kleinen Käferbeinen an dem Flügel festhalten, damit er darauf sitzen bleibt? Übung Nummer 6.1 m = 1· 10-3 kg, r = 15 m, T = 2 s Damit der Käfer die Kreisbewegung mitmachen kann, muss er sich mit der dazu notwendigen Radialkraft an der Flügelspitze festkrallen. Über die Geschwindigkeit ist noch nichts bekannt. Die Bewegung ist aber gleichförmig und Weg und Zeit sind bekannt. Der in 2 Sekunden zurückgelegte Weg ist der Umfang des gesamten Windrades: Übung Nummer 6.1 Damit erhält man die Radialkraft: Damit muss der Käfer eine Kraft aufbringen, die dem 15-fachen seines Körpergewichtes entspricht. Der Käfer muss sich mit 0,15 N festhalten. Übung Nummer 6.1 Übung Nummer 6.1 m = 10 kg, r = 85 m, T = 4 s Mit der Radialkraft: F= 10 𝑘𝑘 ∙ 4 ∙ 𝜋2 85 𝑚 =2.100 𝑁 42 ∙𝑠2 Damit muss eine Kraft aufgebracht werden, die dem 21-fachen dieses Gewichtes entspricht. Übung Nummer 6.2 Turbulenzen beeinflussen den Energieertrag Weibull-Verteilung mit Verschiedenen Parameter (für verschiedene Richtungen eines Standorts) Übung Nummer 6.2 Wind ist bewegte Luft, also ein bewegter gasförmiger Körper mit Masse und Geschwindigkeit der folglich kinetische Energie besitzen muss. Ekin 1 2 = mv 2 Die kinetische Energie kann dem Wind in der Rotorebene eines Windrades entzogen werden und steht an der Rotorwelle als Rotationsenergie zur Verfügung. A Die Größe der Rotorebenenfläche A und die Windgeschwindigkeit v sind die bestimmenden Größen für die Energiegewinnung. Übung Nummer 6.2 m =V ⋅ρ damit wird Die Dichte der Luft beträgt 1 Ekin = V ⋅ ρ ⋅ v 2 2 ρ (20°C ) ≈ 1,2kg / m 3 In der Zeit ∆t durchströmt den Rotor die Luftmasse ∆m mit dem Volumen ∆V. Pwind = Der Zusammenhang zur Fläche A ergibt sich aus der Strömungsgeschwindigkeit v des Windes und dem Volumenstrom ∆V/ ∆t. Welcher proportionaler Zusammenhang besteht zwischen der Windleistung und der Strömungsgeschwindigkeit v des Windes? Ekin , wind ∆t A 1 ρ ⋅ ∆V ⋅ v 2 = 2 ∆t v ∆s = v ⋅ ∆t ∆V = A ⋅ ∆s = A ⋅ v ⋅ ∆t Übung Nummer 6.2 Pwind 1 ρ ⋅ A ⋅ v ⋅ ∆t ⋅ v 2 = 2 ∆t Pwind 1 = ρ ⋅ A ⋅ v3 2 Übung Nummer 6.3 Zwölf Drähte, die alle den gleichen Widerstand von 1 Ω haben, sind so angeordnet, dass sie das Kantenmodell eines Würfels bilden. An zwei Ecken dieses Drahtkantenmodells wird eine elektrische Spannung angelegt. Dabei sind die Ecken so gewählt, dass ihre Verbindungslinie eine Raumdiagonale des Würfels darstellt. a) Fertigen Sie eine Skizze an. In der Skizze müssen der zufließende Strom zum Würfel, der fließende Strom vom Würfel sowie die Teilströme innerhalb der zwölf Drähte des Würfels (Drahtkantenmodell des Würfels) mit ihren Richtungen vorhanden sein. b) Berechnen Sie den Gesamtwiderstand RW des Würfels. Übung Nummer 6.3 zu a) Übung Nummer 6.3 An der Ecke D fließt der gesamte Strom mit der Stromstärke Iges in den Würfel hinein. Da alle 12 Widerstände gleich groß sind und die gesamte Anordnung symmetrisch ist, fließen vom Verzweigungspunkt A drei gleich große Ströme I1, I2, I3 durch die zugehörigen Widerstände R1, R2, R3. Für die Stromstärken gilt: Die Ströme I10, I11, I12 vereinigen sich im Punkt F am "Ausgang des Würfels„ wieder zum Gesamtstrom Iges. Aus den gleichen Symmetriegründen gilt auch für diese Ströme: Übung Nummer 6.3 Der Strom I1 verzweigt sich im Punkt A in die beiden gleich großen Teilströme I4 und I5. Entsprechend verzweigt sich der Strom I2 im Punkt C in die beiden gleich großen Teilströme I6 und I7 und der Strom I3 in die beiden gleich großen Teilströme I8 und I9. Für diese 6 Teilströme gilt: Damit sind die Stärken aller Ströme im Verhältnis zur Gesamtstromstärke Iges festgelegt. Zwischen dem "Eingangspunkt" D des Würfels und dem "Ausgangspunkt F liegt die Spannung UAF.Durch den Würfel mit dem Widerstand RW fließt der Strom mit der Stärke Iges. Es gilt folglich: Gleichung (A) Übung Nummer 6.3 Die Spannung UDF zwischen den Punkten D und F ist unabhängig davon auf welchen Weg im Stromkreis ich von D nach F gelange. Einer dieser Wege wäre z.B. Von D nach A, dann von A nach B und danach von B nach F. Die Spannung UDF, die am Würfel anliegt, ist gleich der Summe der Einzelspannungen, die auf den Teilstrecken abfallen. UDF = UDA + UAB + UBF Ersetzt man die Teilspannungen in dieser Gleichung durch die Produkte aus den Stromstärken und Widerständen, so erhält man: UDF = I1 × R1 + I5 × R5 + I10 × R10 Da alle Widerstände gleich groß sind kann die Indizierung wegfallen und man erhält: Übung Nummer 6.3 Drückt man die einzelnen Stromstärken in dieser Gleichung durch die Stromstärke Iges aus, so folgt: Einsetzen in die Gleichung (A) für den Würfelwiderstand RW ergibt: Der Widerstand des Würfels beträgt:



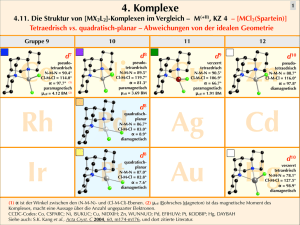
![Hans Walser, [20120912] Kantenmodell des Würfels und des](http://s1.studylibde.com/store/data/011809888_1-7fd94423048ecb4c962cbb407e66d8a8-300x300.png)