4. Komplexe

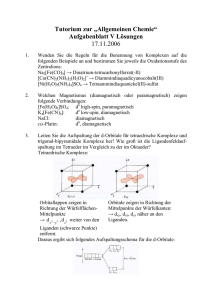
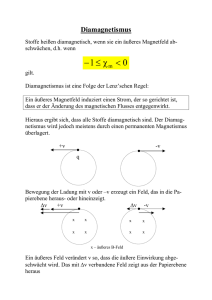
4. Komplexe
1
4.11. Die Struktur von [MX2L2]-Komplexen im Vergleich – M(+II), KZ 4 – [MCl2(Spartein)]
Tetraedrisch vs. quadratisch-planar – Abweichungen von der idealen Geometrie
Gruppe 9
Co
10
d7
pseudotetraedrisch
N-M-N = 90.4°
Cl-M-Cl = 114.0°
α = 97.7° (1)
paramagnetisch
μeff = 4.12 BM (2)
Rh
Ir
11
Ni
d8
pseudotetraedrisch
N-M-N = 89.5°
Cl-M-Cl = 119.7°
α = 81.3°
paramagnetisch
μeff = 3.69 BM
Pd
d8
quadratischplanar
N-M-N = 86.7°
Cl-M-Cl = 83.0°
α = 8.9°
diamagnetisch
Pt
d8
quadratischplanar
N-M-N = 87.0°
Cl-M-Cl = 82.8°
α = 7.6°
diamagnetisch
12
Cu
d9
verzerrt
tetraedrisch
N-M-N = 90.5°
Cl-M-Cl = 106.9°
α = 66.7°
paramagnetisch
μeff = 1.91 BM
Ag
Au
Zn
d10
pseudotetraedrisch
N-M-N = 88.7°
Cl-M-Cl = 116.0°
α = 97.8°
diamagnetisch
Cd
Hg
d10
verzerrt
tetraedrisch
N-M-N = 78.1°
Cl-M-Cl = 127.5°
α = 98.9°
diamagnetisch
(1) α ist der Winkel zwischen den (N-M-N)- und (Cl-M-Cl)-Ebenen. (2) μeff (Bohrsches Magneton) ist das magnetische Moment des
Komplexes, macht eine Aussage über die Anzahl ungepaarter Elektronen.
CCDC-Codes: Co, CSPARC; Ni, ISUKUC; Cu, NIDXIH; Zn, WUNNUO; Pd, EFIHUW; Pt, KODBIP; Hg, DAYBAH
Siehe auch: S.K. Kang et al., Acta Cryst. C 2004, 60, m174-m176, und dort zitierte Literatur.
Konstruktion des "Tetraederwinkels"
Die Kanten des Tetraeders entsprechen den Flächendiagonalen eines umgebenden Würfels.
Tetraeder und Würfel haben einen gemeinsamen Schwerpunkt, den Kreuzpunkt der Raumdiagonalen des Würfels.
Der "Tetraederwinkel" ist der Winkel zwischen Raumdiagonalen des Würfels.