Partneraufgabe - mister mueller

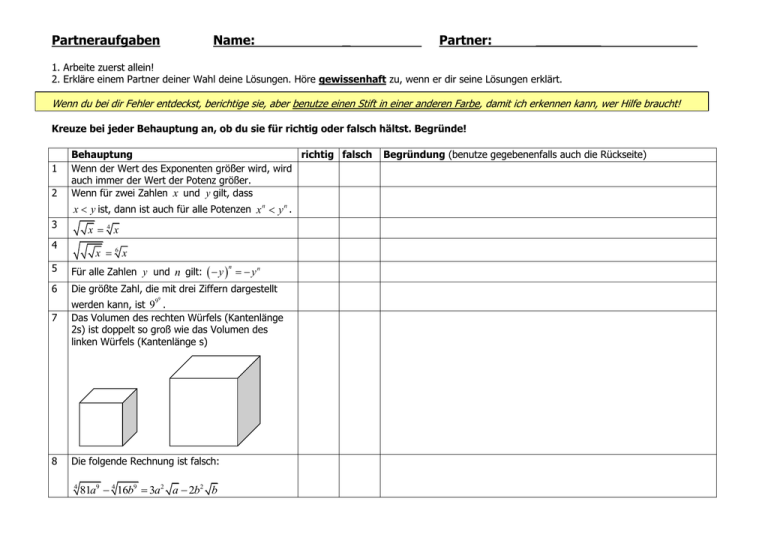
Partneraufgaben
Name:
_
Partner:
________
1. Arbeite zuerst allein!
2. Erkläre einem Partner deiner Wahl deine Lösungen. Höre gewissenhaft zu, wenn er dir seine Lösungen erklärt.
Wenn du bei dir Fehler entdeckst, berichtige sie, aber benutze einen Stift in einer anderen Farbe, damit ich erkennen kann, wer Hilfe braucht!
Kreuze bei jeder Behauptung an, ob du sie für richtig oder falsch hältst. Begründe!
1
2
Behauptung
richtig falsch
Wenn der Wert des Exponenten größer wird, wird
auch immer der Wert der Potenz größer.
Wenn für zwei Zahlen x und y gilt, dass
x  y ist, dann ist auch für alle Potenzen x n  y n .
3
x 4x
4
x 6x
5
Für alle Zahlen y und n gilt:   y    y n
6
Die größte Zahl, die mit drei Ziffern dargestellt
n
9
7
8
werden kann, ist 99 .
Das Volumen des rechten Würfels (Kantenlänge
2s) ist doppelt so groß wie das Volumen des
linken Würfels (Kantenlänge s)
Die folgende Rechnung ist falsch:
4
81a9  4 16b9  3a2 a  2b2 b
Begründung (benutze gegebenenfalls auch die Rückseite)
Partneraufgaben
Musterlösung
Dies sind meine Lösungen der Partneraufgaben, aber ihr wisst, auch ich mache Fehler! Also bitte aufmerksam sein!
Wenn du bei dir Fehler entdeckst, berichtige sie, aber benutze einen Stift in einer anderen Farbe, damit ich erkennen kann, wer Hilfe braucht!
Kreuze bei jeder Behauptung an, ob du sie für richtig oder falsch hältst. Begründe!
1
Behauptung
richtig falsch
Wenn der Wert des Exponenten größer wird, wird
x
auch immer der Wert der Potenz größer.
Begründung (benutze gegebenenfalls auch die Rückseite)
2
1
1
1
Ein Beispiel: a  , zuerst nehme ich als Exponent 2.    . Mit
4
2
2
3
1
1
dem Exponent 3 ist der Wert der Potenz aber kleiner:    .
2
Wenn für zwei Zahlen x und y gilt, dass
x
x  y ist, dann ist auch für alle Potenzen x  y .
n
3
4
x
x 4x
1
1 1
1
 1 2

x x2   x2 2  x4  4 x
 
 
x
x  x
6
5
Für alle Zahlen y und n gilt:   y    y n
6
Die größte Zahl, die mit drei Ziffern dargestellt
n
9
7
n
8
2
Für negative Exponenten stimmt das nicht, wie folgendes Beispiel zeigt:
1 1 1 1
2  3 , aber 2  2  2    2  3  2 .
4 9 3
2
werden kann, ist 99 .
Das Volumen des rechten Würfels (Kantenlänge
2s) ist doppelt so groß wie das Volumen des
linken Würfels (Kantenlänge s)
1
 1 1 2
1
1 1 1
  2 
 
2
2
2
2


 x
x  x
 x8  8 x
   


x
x
99  999  981  999
x
Das Volumen des großen Würfels ist (2s) 3  8s 3 , das de kleinen s 3 .
(2) 2  4 , aber  (2) 2  4
9
Damit ist der große Würfel achtmal größer.
8
Die folgende Rechnung ist falsch:
4
81a  16b  3a
9
4
9
2
a  2b
2
x
Richtig wäre:
1
4
b
1
81a 9  4 16b 9  (81a 9 ) 4  (16b 9 ) 4
1
 81 4
9
a4
1
 16 4
9
b4
8
1
8
1
 3a 4 a 4  2b 4 b 4
 3a  4 a  2b 2  4 b