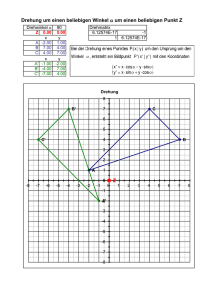
Elementare Geometrie - Universität Münster

Westfälische Wilhelms-Universität Münster
Mathematisches Institut
Übungen zur Vorlesung
Elementare Geometrie
Sommersemester 2010
Musterlösung zu Blatt 12
vom 5. Juli 2010
apl. Prof. Dr. Lutz Hille
Dr. Karin Halupczok
erstellt von M. Holl, M. Möller, F. Springer, K. Halupczok
Zu Aufgabe 1:
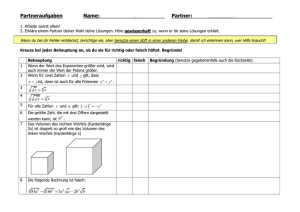
Widerlegen Sie die folgenden falschen Behauptungen durch Angabe eines möglichst einfachen Gegenbeispiels:
(a) Jede orthogonale Abbildung bildet einen Vektor 6= 0 auf sein Negatives ab.
(b) Jede Gleitspiegelung ist die Komposition aus zwei zentrischen Streckungen.
(c) Jede affine Abbildung bildet Kreise auf Kreise ab.
(d) Jede Spiegelung, die ein regelmäßiges n-Eck auf sich abbildet, bildet auch mindestens
einen der Eckpunkte auf sich ab.
Lösung:
R → R ist orthogonal, aber id(1) = 1 6= −1
(b): Betrachte R2 . Sei σ die Spiegelung an einer beliebigen (aber fest gewählten)
Zu (a): id :
Zu
Achse. Dann ist σ eine Gleitspiegelung. Als orientierungsumkehrende Abbildung kann sie
nicht Komposition zweier orientierungserhaltenden Abbildungen sein, insbesondere also
nicht Komposition zweier zentrischer Streckungen.
x
2
2
Zu (c): Man betrachte die lineare (und somit auch affine) Abbildung f :
→ ,
7→
y
2x
. Diese bildet Kreise auf echte Ellipsen ab.
y
R
R
Zu (d): Seien A, B, C, D die Eckpunkte eines Quadrats und σ die Spiegelung an der
Geraden durch die Mittelpunkte von AB und CD. Dann gilt σ(ABCD) = ABCD,
aber σ(X) = X für alle X ∈ {A, B, C, D}.
1
Zu Aufgabe 2:
Einem Würfel der Kantenlänge a wird ein Tetraeder so einbeschrieben, dass die Tetraederkanten Diagonalen der Würfelflächen sind. Man betrachte eine Ebene, die im Abstand
a
parallel zu zwei Würfelseiten liegt. Zeigen Sie:
2
(a) Der Schnitt der Ebene mit dem Tetraeder ist ein Quadrat, dessen Seitenlänge die
halbe Kantenlänge des Tetraeders beträgt.
(b) Die Ebene schneidet das Tetraeder in zwei kongruente Teile.
Lösung:
Zu (a): O.B.d.A. sind die Koordinaten des Würfels die folgenden: (0, 0, 0), (a, 0, 0),
(0, a, 0), (0, 0, a), (a, a, 0), (a, 0, a), (0, a, a), (a, a, a),
des Tetraeders: (0, 0, 0), (a, a, 0), (0, a, a), (a, 0, a),
und die Ebene ist gegeben durch:
 
a
 
0
0
2
E =  0 + s  0 + t  a2 
a
0
0
2
Berechne nun die Schnittpunkte der Geraden, auf denen die Tetraederseiten liegen, mit
dieser Ebene:
 
a

1. Gerade durch (0, 0, 0), (a, 0, a) ist r 0
a
   
a
 
a
a
0
0
2
2
r 0 =  0 + s  0 + t  a2  ⇒ SP =  0
a
a
a
0
0
2
2
 
 
0
0



2. Gerade durch (0, 0, 0), (a, 0, a) ist r a ⇒ SP = a2 
a
a
2
 
 
 
a
0
a
3. Gerade durch (a, a, 0), (a, 0, a) ist 0 + r  a ⇒ SP =  a2 
a
a
−a
2
 
 
a
a
a
2



0 ⇒ SP =  a
4. Gerade durch (a, a, 0), (a, a, a) ist a + r
a
0
−a
2
⇒ Diese Schnittpunkte
√ bilden, wie man leicht sieht oder nachrechnet, ein Quadrat mit
Seitenlänge √a2 = 21 2a = 21 · Diagonalenlänge einer Fläche des Würfels = 12 Kantenlänge
des Tetraeders.
2
Zu (b): Spiegelung an der aus (a) gegebenen Ebene lässt die Schnittpunkte aus (a) fix, da
diese auf der Spiegelebene liegen, und schickt offensichtlich die Eckpunkte des Würfels auf
die gegenüberliegenden Eckpunkte. Schließt man an diese Spiegelung noch eine Drehung
um 90◦ um die Achse senkrecht zur Ebene durch zwei Flächenmittelpunkte an, so erkennt
man, dass dadurch die beiden Tetraederteile ineinander übergehen. Dies ist offensichtlich
eine Kongruenzabbildung. ⇒ Die beiden Teile sind kongruent.
Zu Aufgabe 3:
Auf die Seitenflächen eines Würfels der Kantenlänge a werden quadratische Pyramiden
aufgesetzt. Wie hoch sind diese Pyramiden zu wählen, damit ein regelmäßiges Polyeder
mit 12 kongruenten Rauten als Seitenflächen entsteht?
Lösung:
Wir betrachten das Dreieck, das durch die Mittelpunkte zweier gegenüberliegender Kanten
auf einer Seitenfläche und die zugehörige Pyramidenspitze definiert ist. Dieses Dreieck
muss gleichschenklig sein, damit die Pyramide gerade ist. Der Basiswinkel muss 45◦ groß
sein, damit für die Seitenfläche der Pyramide mit der entsprechenden Seitenfläche der
anliegenden Pyramide eine Raute entsteht und die beiden „Dreiecksflächen“ einen Winkel
von 180◦ einschließen (90◦ + 45◦ + 45◦ , rechter Winkel des Würfels und die beiden Winkel
der Dreiecke). Somit beträgt das Maß der Winkel des Dreiecks an der Pyramidenspitze
ebenfalls 90◦ . Nach dem Satz des Thales liegt die Dreiecksspitze auf einem Halbkreis um
den Mittelpunkt der Verbindungsstrecke (Länge a) und gerade über diesem. Die Höhe des
Dreiecks entspricht also dem Radius des Thaleskreises, welcher a2 beträgt.
Zu Aufgabe 4:
Schreiben Sie die 12 Elemente der alternierenden Gruppe A4 als Produkt der Transpositionen (12), (13), (14).
Lösung:
1 2 3 4
= (12)(12)
1 2 3 4
3
1
2
1
3
1
4
1
1
1
1
1
3
1
4

2 3 4

= (12)(34) = (12)(13)(14)(13)


1 4 3



 Drehung um 180◦ um Ach2 3 4
= (13)(24) = (13)(12)(14)(12) sen durch Mittelpunkte ge4 1 2


genüberliegender Kanten



2 3 4

= (14)(23) = (14)(12)(13)(12)

3 2 1

2 3 4

= (24)(23) = (12)(14)(12)(12)(13)(12) = (12)(14)(13)(12)
 Drehung um
3 4 2
Symmetrieachse

2 3 4

= (23)(24) = (12)(13)(12)(12)(14)(12) = (12)(13)(14)(12) durch 1
4 2 3

2 3 4

= (14)(13)

2 4 1
Drehung um Symmetrieachse durch 2

2 3 4

= (13)(14)
2 1 3
1
2
1
4

2 3 4

= (14)(12)

4 3 1
Drehung um Symme

trieachse durch 3
2 3 4

= (12)(14)
1 3 2
1
2
1
3
2 3
3 1
2 3
1 2
4
1
3

4

= (13)(12)

4
Drehung um Symmetrieachse durch 4

4

= (12)(13)
4
* Letzte Aufgabe *
Welche Ornamentgruppe hat die folgende Figur als Fundamentalbereich?
(a)
(b)
4
2
Lösung:
Zu (a): Zwei der Teile lassen sich mit zwei gespiegelten Teilen zu einem translativen
Bereich zusammensetzen:
Die eingezeichneten Geraden durch die Teile sind Achsen von Gleitspiegelungen, die das
Muster in sich überführen. Es sind keine Spiegelungen oder Rotationen möglich, die dies
schaffen. Daher haben wir die Ornamentgruppe pg vorliegen.
Zu (b):
Die Teile lassen sich so zusammensetzen, dass pro Teil drei Drehzentren erkennbar sind,
die das Muster in sich überführen (dabei wird jeweils um 120◦ gedreht). Es sind keine
Spiegelungen oder Gleitspiegelungen oder weitere Drehungen möglich, die das Muster in
sich überführen. Daher haben wir die Ornamentgruppe p3 vorliegen.
Die interaktive Webseite zum Malen in Ornamentgruppen:
http://www.imaginary2008.de/interaktiv/Ornamente/Ornamente.html
5