Partneraufgaben Musterlösung

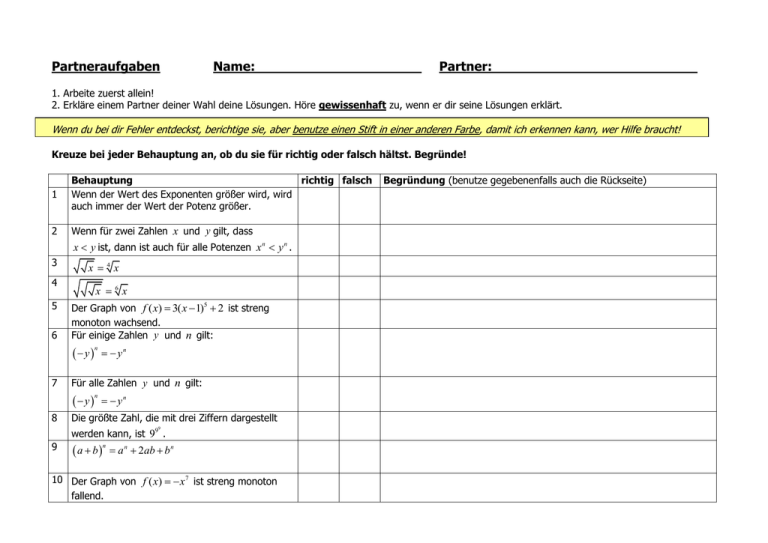
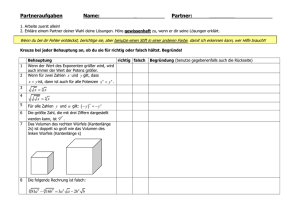
Partneraufgaben
Name:
_
Partner:
________
1. Arbeite zuerst allein!
2. Erkläre einem Partner deiner Wahl deine Lösungen. Höre gewissenhaft zu, wenn er dir seine Lösungen erklärt.
Wenn du bei dir Fehler entdeckst, berichtige sie, aber benutze einen Stift in einer anderen Farbe, damit ich erkennen kann, wer Hilfe braucht!
Kreuze bei jeder Behauptung an, ob du sie für richtig oder falsch hältst. Begründe!
1
Behauptung
richtig falsch
Wenn der Wert des Exponenten größer wird, wird
auch immer der Wert der Potenz größer.
2
Wenn für zwei Zahlen x und y gilt, dass
x  y ist, dann ist auch für alle Potenzen x n  y n .
3
x4x
4
5
6
x 6x
Der Graph von f ( x)  3( x  1)5  2 ist streng
monoton wachsend.
Für einige Zahlen y und n gilt:
 y
7
  yn
Für alle Zahlen y und n gilt:
 y
8
n
n
  yn
Die größte Zahl, die mit drei Ziffern dargestellt
9
werden kann, ist 99 .
9
a  b
n
 a n  2ab  b n
10 Der Graph von f ( x)   x 7 ist streng monoton
fallend.
Begründung (benutze gegebenenfalls auch die Rückseite)
11 Das Volumen des rechten Würfels (Kantenlänge
2s) ist doppelt so groß wie das Volumen des
linken Würfels (Kantenlänge s)
12 Die folgende Rechnung ist falsch:
81a9  4 16b9  3a2 a  2b2 b
13 Für alle relle Zahlen x und ganze Zahlen n gibt
es die Potenz x n
14 Die Graphen der Funktionen f ( x)  x n und der
Funktion g ( x)  a  x n haben für jedes a (außer
a  0 ) immer das gleiche Monotonieverhalten.
15 Die Graphen der Funktionen f ( x)  x n und der
Funktion g ( x)  a  x n haben für jedes a (außer
a  0 ) immer die gleiche Symmetrie.
4
Partneraufgaben
Musterlösung
1. Arbeite zuerst allein!
2. Erkläre einem Partner deiner Wahl deine Lösungen. Höre gewissenhaft zu, wenn er dir seine Lösungen erklärt.
Wenn du bei dir Fehler entdeckst, berichtige sie, aber benutze einen Stift in einer anderen Farbe, damit ich erkennen kann, wer Hilfe braucht!
Kreuze bei jeder Behauptung an, ob du sie für richtig oder falsch hältst. Begründe!
Begründung (benutze gegebenenfalls auch die Rückseite)
1
Behauptung
richtig falsch
Wenn der Wert des Exponenten größer wird, wird
auch immer der Wert der Potenz größer.
x
1
1 1
1
Zum Beispiel:    , aber   
2 8
 2  16
2
Wenn für zwei Zahlen x und y gilt, dass
x
Zum Beispiel: 4  3 , aber (4)4  256  81  34
x  y ist, dann ist auch für alle Potenzen x n  y n .
3
x
x4x
4
3
1
1 1
1
 1 2
x   x2   x2 2  x4  4 x
 
x
x 6x
5
Der Graph von f ( x)  3( x  1)5  2 ist streng
monoton wachsend.
6
Für einige Zahlen y und n gilt:
4
x
1
 1 12  2
1
1 1 1
 
x    x 2    x 2 2 2  x8  8 x


  


Der Graph von f ( x)  x5 ist streng monoton wachsend. Der Graph von
f ( x)  3( x  1)5  2 ist nach oben und nach rechts verschoben und dann
gestreckt worden, die Monotonie bleibt die gleiche.
 y
7
  yn
n
Zwei Beispiele:  5    5   5   5   125  53 , und ebenso
3
 2 
Für alle Zahlen y und n gilt:
 y
8
n
x
x
  yn
Die größte Zahl, die mit drei Ziffern dargestellt
9
werden kann, ist 9 .
9
x
5
 32  25
Ein Gegenbeispiel genügt:  2   16 , aber 24  16
4
99  9
9
9  . Man könnte denken 99  99 9  981  999 , aber das ist falsch die
9
9
9
9
a  b
n
x
 a n  2ab  b n
10 Der Graph von f ( x)   x 7 ist streng monoton
fallend.
11 Das Volumen des rechten Würfels (Kantenlänge
2s) ist doppelt so groß wie das Volumen des
linken Würfels (Kantenlänge s)
x
x
9 
9
Klammern müssen so gesetzt werden: 99  9
Das ist nur für n  2 richtig. Schon für n  3 stimmt es nicht mehr, denn:
 a  b
3
  a  b  a  b  a  b   a 3  3a 2b  3ab 2  b3
Der Graph von f ( x)  x7 ist streng monoton wachsend, durch das – wird
der Graph an der x-Achse gespiegelt, also wird er streng monoton fallend.
Das Volumen des kleinen Würfels errechnet man als
Vklein  s 3 .
Das Volumen des großen Würfels ist aber
Vgroß  (2s)3  23 s3  8s3 .
Also ist das Volumen des rechten Würfels achtmal so groß wie das des
kleinen Würfels.
12 Die folgende Rechnung ist falsch:
x
Richtig wäre:
81a9  4 16b9  3a2 a  2b2 b
13 Für alle relle Zahlen x und ganze Zahlen n gibt
es die Potenz x n
x
14 Die Graphen der Funktionen f ( x)  x n und der
x
4
81a9  4 16b9  3a2 4 a  2b2 4 b
4
Funktion g ( x)  a  x haben für jedes a (außer
a=0) immer das gleiche Monotonieverhalten.
15 Die Graphen der Funktionen f ( x)  x n und der
eine andere Schreibweise für
n
Funktion g ( x)  a  x n haben für jedes a (außer
a=0) immer die gleiche Symmetrie.
Das ist beinahe richtig, aber es gibt mindestens ein Problem, denn 0 1 ist
x
1
, und teilen durch 0 ist nicht erlaubt.
0
Für negative Werte von a wird der Graph an der x-Achse gespiegelt und
dadurch ändert sich das Monotonieverhalten (aus streng monoton
wachsend wird streng monoton fallend).
Durch Stauchen, Zerren oder Spiegeln an der x-Achse bleibt die
Symmetrie erhalten.