Musterprüfung – Lösungen 1. (a) Mit z1 = 1 + 3 j, z2 = 2 − j und z3

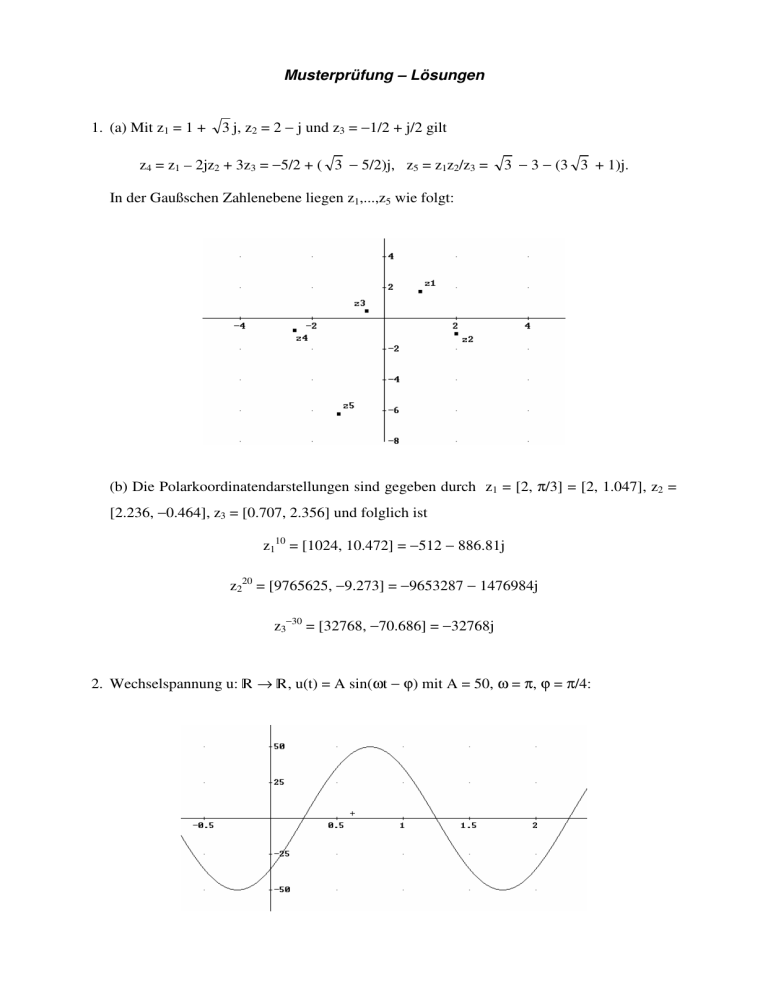
Musterprüfung – Lösungen
1. (a) Mit z1 = 1 +
3 j, z2 = 2 − j und z3 = −1/2 + j/2 gilt
z4 = z1 – 2jz2 + 3z3 = −5/2 + ( 3 − 5/2)j, z5 = z1z2/z3 =
3 − 3 − (3 3 + 1)j.
In der Gaußschen Zahlenebene liegen z1,...,z5 wie folgt:
(b) Die Polarkoordinatendarstellungen sind gegeben durch z1 = [2, π/3] = [2, 1.047], z2 =
[2.236, −0.464], z3 = [0.707, 2.356] und folglich ist
z110 = [1024, 10.472] = −512 − 886.81j
z220 = [9765625, −9.273] = −9653287 − 1476984j
z3−30 = [32768, −70.686] = −32768j
2. Wechselspannung u: — → —, u(t) = A sin(ωt − ϕ) mit A = 50, ω = π, ϕ = π/4:
Dabei gibt A die Amplitude an, d.i. die maximale Auslenkung in vertikaler Richtung, ω ist
die Kreisfrequenz und beschreibt die Anzahl der Schwingungen in einem Intervall der
Länge 2π, und ϕ ist die Phasenverschiebung, welche eine Verschiebung der Kurve in
horizontaler Richtung steuert.
Die Funktion u ist weder injektiv noch surjektiv, da einerseits die Funktionswerte im
Intervall [−A, A] unendlich viele Urbilder besitzen, andererseits die Werte außerhalb
dieses Intervalls überhaupt keine. Eine geeignete Einschränkung von u, welche sowohl
injektiv als auch surjektiv ist, ist etwa durch u: [−0.25, 0.75] → [−50, 50] gegeben.
3. (a) Die ersten Glieder der Folge
2n 2 − 1
, n = 1,2,3,...
xn =
2n 2 + 1
sind x1 = 0.333, x2 = 0.778, x3 = 0.895, x4 = 0.939, x5 = 0.961, usw. Die Folge ist streng
monoton wachsend, denn
x n < x n +1
2n 2 − 1 2(n + 1) 2 − 1
⇔
<
2n 2 + 1 2(n + 1) 2 + 1
⇔ (2n 2 − 1)(2n 2 + 4n + 3) < (2n 2 + 1)(2n 2 + 4n + 1)
⇔ 4 n 4 + 8n 3 + 4 n 2 − 4 n − 3 < 4 n 4 + 8n 3 + 4 n 2 + 4 n + 1
⇔ 8n + 4 > 0
und (nach unten und nach oben) beschränkt, denn
0 < xn =
2n 2 − 1 2n 2 + 1
<
=1
2n 2 + 1 2 n 2 + 1
für alle n ∈ Õ. Folglich ist (xn) auch konvergent, der Grenzwert lautet
1
2n − 1
n 2 = 1.
lim x n = lim 2
= lim
n →∞
n → ∞ 2n + 1
n →∞
1
2+ 2
n
2
2−
(b) Allgemein nennt man eine Folge (xn) streng monoton wachsend, wenn xn < xn+1, streng
monoton fallend, wenn xn > xn+1, monoton wachsend, wenn xn ≤ xn+1, und monoton
fallend, wenn xn ≥ xn+1. Die Folge (xn) ist beschränkt, wenn es Zahlen a, b gibt, sodass a ≤
xn ≤ b für alle n ∈ Õ gilt. Schließlich heißt die Folge (xn) konvergent mit dem Grenzwert c,
falls in jeder ε-Umgebung von c fast alle Glieder der Folge liegen, d.h., falls es zu jedem
ε > 0 einen Index N(ε) gibt, sodass gilt
|xn − c| < ε für alle n ≥ N(ε).
4. Man berechnet den Barwert B zum Auszahlungszeitpunkt gemäß
B = K0 + E
(1 + r ) n − 1
r (1 + r ) n
und erhält für die Variante A mit K0 = 80000 und E = 0 den Auszahlungsbetrag BA =
80.000,- sowie für die Variante B mit K0 = 35000, E = 5000, n = 12 und r = 0,035 den
Auszahlungsbetrag BB = 83.316,67. Für die Variante C folgt mit B = K0 + E/r, K0 = 25000,
E = 2000 und r = 0,035 letztlich BC = 82.142,86. Am günstigsten für den Sparer ist somit
die Variante B.
Nun, hätten Sie alles richtig? Ihre Punktezahl und Ihre Note können Sie auf Grund der
Angaben zu den Prüfungsbeispielen selbst ermitteln. Alles Gute für die erste „richtige“
Prüfung am Semesterende!
G.K.