Lösung Test 09/2015

13. Jgst.
1. Test
Kurs 13/3
Thema:
Fach: Mathematik (Grundfach)
Grundlagen W‘keitsrechnung;
Baumdiagramm; Pfadregeln
Bitte geben Sie Ansätze und Rechenwege an!
Aufgabe 1:
Datum: 30.09.2015
Name:
Punkte:
Note:
Begriffe und Fragen rund um die Wahrscheinlichkeit
9
a) Beschreiben Sie folgende Begriffe:
(i)
Unmögliches Ereignis
Lösung:
Ein Unmögliches Ereignis A ist ein Ereignis, das bei jeder Ausführung eines Zufallsexperiments niemals eintreten kann. Die Wahrscheinlichkeit für das Eintreten jedes
unmöglichen Ereignisses ist stets gleich Null: P(A) = 0.
Beispiel für ein unmögliches Ereignis:
Beim Zufallsexperiment Zweimaliges Werfen eines Würfels ist das Ereignis
A = Summe der beiden Augenzahlen ist gleich Null
ein unmögliches Ereignis.
(ii)
Ergebnismenge
Lösung:
Die Ergebnismenge ist die Zusammenfassung aller möglichen Ergebnisse in einer Menge. Beim Würfeln ist also Ω= {1; 2; 3; 4; 5; 6} die Ergebnismenge.
(iii)
Schnittmenge
Lösung:
Die Schnittmenge A∩B zweier Mengen A und B ist die Menge aller Elemente, die sowohl zu A als auch zu B gehören: A∩B={x | x ∈ A ∧ x ∈ B}
b) Welche Werte kann die Wahrscheinlichkeit eines Ereignisses nicht annehmen?
Begründen Sie Ihre Antwort.
Lösung:
Alle Zahlen außerhalb des Intervalls [0 ; 1] können als Wahrscheinlichkeit nicht angenommen werden, da dies gegen die Definition der Laplacewahrscheinlichkeit verstoßen
würde: Anzahl der günstigen Ergebnisse / Anzahl der möglichen Ergebnisse
Aufgabe 2:
Mengen und Mengenoperationen
9
Im Supermarkt ist Obsttag. Von insgesamt 100 Testkäufern kaufen 95 % Obst.
70 Personen kaufen Äpfel (Menge A) und 45 kaufen Birnen (=Menge B).
a) Bilden Sie die Gesamtsituation in einem Mengendiagramm ab.
Lösung:
5
50
25
20
B
A
Bestimmen Sie nun die Anzahl der Personen gemäß folgender Mengendarstellungen und beschreiben Sie die gesucht Menge:
b)
A B
c)
A\ B
d)
A B
Lösung:
A B
A\ B
A B
 95
 50
 80
Testkäufer kaufen Äpfel oder Birnen oder beides.
Testkäufer kaufen Äpfel aber keine Birnen.
Testkäufer kaufen nicht „Äpfel und Birnen“.
S=100
Aufgabe 3:
Baumdiagramm & Pfadregeln
12
Die Hochschule hält eine Eingangsprüfung im Wahlfach Englisch ab.
Die Prüfung besteht aus 3 Fragen mit jeweils 5 Aussagen, von denen genau
eine richtig ist.
Die Prüfung ist bestanden, wenn mindestens 2 richtige Antworten angekreuzt
wurden. Ein Kandidat versucht die Prüfung durch Raten zu bestehen.
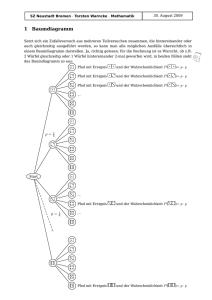
a) Zeichnen Sie ein vollständiges Baumdiagramm.
Lösung:
Dreistufiges Baumdiagramm mit jeweils zwei Verzweigungen (R / F) und den Wahrscheinlichkeiten 0,2 für Richtig und 0,8 für Falsch.
Insgesamt entstehen acht Pfade bzw. Ausgänge.
b) Bestimmen Sie die Wahrscheinlichkeit, mit der der Kandidat besteht.
Lösung:
P "mind. 2 Richtige"  P  X  2   P  X  3
 P  X  2   P  X  3  3  0, 22  0,8  0, 23
 0,104
Aufgabe 4:
8
Ein Glücksrad besteht aus vier Kreissektoren, die mit den
Zahlen 1, 2, 3 und 4 versehen sind.
Die Mittelpunktswinkel der verschiedenen Sektoren haben
die Weiten 30 °, 60 °, 90 ° und 180 ° (siehe Abbildung).
Nach jeder Drehung gilt diejenige Zahl als gezogen, auf deren Kreissektor der feststehende Pfeil zeigt.
a) Wie groß ist Wahrscheinlichkeit, die vierstellige Zahl 1234 bei vier Drehungen
zu erhalten?
Lösung:
P "1234" 
30 60 90 180



360 360 360 360

1 1 1 1
  
12 6 4 2

1
576
b) Wie groß ist die Wahrscheinlichkeit, eine Zahlenkombination aus vier verschiedenen Ziffern bei vier Drehungen zu erhalten?
Lösung:
P "Permutation zu 1234"  4! 
1
576
 24 
1
576

1
24
Aufgabe 5:
Wahrscheinlichkeit mit Murmel-Hans
12
Hans hat in seiner Hosentasche 7 rote, 8 grüne und 5 blaue gleich große Murmeln.
Er zieht eine Murmel.
Wie groß ist die Wahrscheinlichkeit,
a) eine rote aus der Hosentasche zu ziehen?
Lösung:
P "rot" 
7
20
 0,35
b) eine grüne oder eine blaue Murmel aus der Hosentasche zu ziehen?
Lösung:
P "grün  blau" 
13
20
 0, 65
Hans zieht nacheinander zwei Murmeln ohne Zurücklegen.
Mit welcher Wahrscheinlichkeit zieht er
c) zwei rote Murmeln?
Lösung:
P "r,r" 
7 6

20 19
21
190

 0,1105
d) zwei gleichfarbige Murmeln?
Lösung:
P "r,r"  P "g,g"  P "b,b" 
7 6
8 7
5 4
    
20 19 20 19 20 19

59
190
 0,3105
Hans zieht nun zwei Murmeln mit Zurücklegen.
e) Betrachten Sie die Wahrscheinlichkeit für das Ereignis „Ziehen zweier gleichfarbiger Kugeln“.
Beurteilen Sie, ob diese größer oder kleiner als beim Ziehen ohne
Zurücklegen ist (mit Begründung!).
Lösung:
Die Wahrscheinlichkeit für gleichfarbige Kugeln wird größer, da beim Ziehen ohne
Zurücklegen die Reduzierung im Zähler prozentual größer ist, als die Reduzierung im
Nenner; damit wird der Bruch vom Wert her kleiner als beim Ziehen mit Zurücklegen.