Glossar Wahrscheinlichkeitsrechnung
Werbung

Glossar Wahrscheinlichkeitsrechnung
Absolute und relative Häufigkeiten:
Absolute und relative Häufigkeiten werden bei Zufallsexperimenten erfasst. Wird mit einem Würfel
gewürfelt, kann die absoluten und relative Häufigkeiten für das Auftreten der Sechs in einer Tabelle
erfasst werden.
Nummer
Würfelergebnis
Ereignis
Abs. Häufigkeit
1
2
3
4
3
4
1
6
4
Nein
Nein
Nein
Ja
Nein
0
0
0
1
1
5
Relative Häufigkeit
0 von 1
0 von 2
0 von 3
1 von 4
1 von 5
0
0
0
0,25
0,2
Ergebnis, Ergebnisraum, Ereignis:
Mit einem Würfel kann ich die Augenzahlen 1,2,3,4,5 und 6 würfeln. Mit jedem Wurf erhalte ich
ein Ergebnis dieses Zufallsversuchs. Die Menge {1,2,3,4,5,6} bilden zusammen den Ergebnis­
raum.
Ein Ereignis beschreibt die Erwartungshaltung eines Spielers beim Würfeln. Wenn dieser Spieler
mit einer Zwei oder einer Vier weiter kommt, so wartet er auf das Ereignis {2 ober 4}. Ein Ereignis
kann sich aus einem oder mehreren Ergebnissen zusammen setzen.
Wahrscheinlichkeit:
Die Wahrscheinlichkeit eines Ereignisses wird mit einem Zahlenwert zwischen Null und Eins
beschrieben. Der Zahlenwert Null beschreibt das unmögliche Ereignis, der Zahlenwert Eins die
Gewissheit.
p E=
Anzahl der günstigen Ergebnisse
Anzahl aller Ergebnisse
Wahrscheinlichkeiten können mit Brüchen, Dezimalbrüchen oder auch Prozentwerten angeben
werden.
Laplace Wahrscheinlichkeit:
Von einem Laplace-Experiment spricht man, wenn die Ergebnisse alle gleichwahrscheinlich sind.
Diese Gleichwahrscheinlichkeit bestimmt man i.d.R. durch die geometrische Anordnung des
Zufallsgeräts.
Gegenwahrscheinlichkeit:
Die Wahrscheinlichkeit eines Ereignisses E und seine Gegenwahrscheinlichkeit E ergänzen sich
zum Zahlenwert 1. Die Gegenwahrscheinlichkeit ist die Wahrscheinlichkeit des Gegenereignisses.
1
Glossar Wahrscheinlichkeitsrechnung
Baumdiagramm:
Das Baumdiagramm ist das grundlegende Arbeitsmittel in der Sekundarstufe I in der Wahrschein­
lichkeitsrechnung. Bei einem mehrstufigen Zufallsversuch werden die häufig gleichzeitig
stattfindenden Versuchsergebnisse in zwei Phasen strukturiert und hintereinander angeordnet. Im
Folgenden wird das Würfeln mit zwei Würfeln als Baumdiagramm dargestellt.
Blauer
Würfel
Roter
Würfel
Die Wahrscheinlichkeiten für ein Ergebnis werden auf die Äste des Baumdiagramms geschrieben.
Die Ergebnisse stehen an die Enden der Äste.
Maultpikations- oder Pfadregel:
Bewegt man sich auf einem Pfad, so werden die Wahrscheinlichkeiten der einzelnen Äste zur
2
Glossar Wahrscheinlichkeitsrechnung
Endwahrscheinlichkeit multipliziert.
Additionsregel:
Die Wahrscheinlichkeiten einer Verzweigung lassen sich zu Eins addieren.
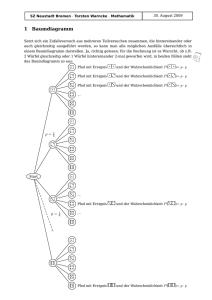
Verkürztes Baumdiagramm:
Ein verkürztes Baumdiagramm entsteht, wenn man Äste weg lässt oder zusammen fasst. Nur das zu
betrachtende Ereignis wird dargestellt. Die Verkürzungen sind notwendig, weil oft ein vollständiges
Baumdiagramm oft nicht darstellbar ist. Im Folgenden ist ein verkürztes Baumdiagramm für das
Würfeln mit zwei Würfeln und das Ereignis „8“ dargestellt.
Blauer Würfel
E
1
Roter Würfel
1
x
2
6
3
5
4
4
5
3
6
2
1
1
6
1
6
1
6
2
3
1
6
1
6
1
6
4
5
6
1
6
E
5
6
E
1
6
E
5
6
E
1
6
E
5
6
E
1
6
E
5
6
E
1
6
E
5
6
E
Erwartungswert:
Bei Gewinnspielen kann Geld gewonnen werden. Wird die Wahrscheinlichkeit eines Ereignisses
mit dem zu erwartenden Gewinn multipliziert, so erhält man den Erwartungswert – die durch­
schnittliche Gewinnerwartung dieses Ereignisses. Erwartungswerte gibt es nicht nur beim Glücks­
spiel. Man erhält sie durch die Multiplikation der Wahrscheinlichkeit mit der zugeordneten Größe.
3