Wasserstoff-ähnliche Atome

Kapitel III
Wasserstoff-ähnliche Atome
Dieses Kapitel1 ist dem Atom und seiner theoretischen Beschreibung gewidmet. In der Atomphysik betrachtet man quantenmechanische Zustände von atomaren Schalen. Das einfachste und
am meisten studierte Problem ist das Problem des Wasserstoff-Atoms. In erster Näherung kann
man das Wasserstoff-Atom als ein nicht-relativistisches System von zwei Teilchen, ein Proton
(oder allgemeiner ein positiver Kern) und ein Elektron, die miteinander durch die CoulombWechselwirkung gebunden sind, betrachten. Dieses einfaches Problem kann man mit Hilfe
der Schrödinger-Gleichung lösen, und damit die Energie-Niveaus des Wasserstoff-Atoms finden.
Die Schrödinger-Gleichung liefert die Energie-Niveaus, die schon von dem Bohr-Modell bekannt
waren. Allerdings, selbst wenn das theoretisch berechnete Wasserstoff-Atom Energiespektrum
grob dem Experiment entspricht, ist die Übereinstimmung weit von perfekt und für eine exacte
Beschreibung muss man das Problem relativistisch betrachten. Eine relativistische Beschreibung
des Wasserstoff-Atoms ist durch die Dirac Gleichung gegeben.
Die Dirac-Gleichung berücksichtigt den Spin vom Elektron, ein Effekt der rein relativistisch
ist. Damit kann man die Feinstruktur der atomaren Spektren erklären. Weitere Korrekturen
zu den von der Dirac-Gleichung gegebenen atomaren Niveaus wie die Lamb-Verschiebung und
die Hyperfeinstruktur beziehen sich auf der Kopplung des Elektrons zu dem Strahlungsfeld und
dem Kernspin. Auch die Kerneigenschaften, wie z.B. seine Masse und räumliche Ausdehnung
können die Spektren von Atomen beeinfüssen. In den folgenden Abschnitten wollen wir eine
Einführung in der Theorie des ein-Elektron-Systeme (also Wasserstoff-Atome oder Wasserstoffähnliche Ionen) geben und einiges über die Dirac-Gleichung und die weiteren Korrekturen, die
in den Atomarenspektren zu sehen sind, erläutern.
III.1
Die Suche nach einer relativistischen Quantenmechanik
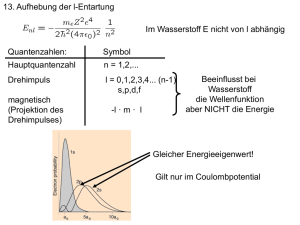
Die Schrödinger-Gleichung für das Wasserstoff-Atom, die bereits in der QuantenmechanikVorlesung angesprochen und gelöst worden ist, betrachtet nicht relativistisch das Problem eines
Elektrons in einem vom positiven Kern erzeugten Zentralfeld. Dieses Problem hat eine radiale Symmetrie und kann sehr schön in Kugelkoordinaten gelöst werden. Damit kann man die
Wellenfunktion des Elektrons erfahren, Ψ(r, θ, φ) = Rnl (r) Ylm (θ, φ), die von der Hauptquantenzahl n, der Drehimpulsquantenzahl l, l = 0, 1, 2, ..., n − 1 und der magnetische Quantenzahl ml ,
ml = −l, l + 1, ..., 0..., l − 1, l bestimmt wird. Die entsprechende Energie des atomaren Zustandes
1
Herzlichen Dank an Kristian Haberkorn, denn ohne seine Hilfe wäre dieses Kapitel nicht so schön auf Deutsch
geschrieben!
3
4
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
ist allerdings entartet und hängt nur von der Hauptquantenzahl n ab, in atomaren Einheiten,
En = −
Z2
,
2n2
(III.1)
wobei Z die Kernladung ist. Um diese (l, m) Entartung zu erheben, muss man die Symmetrie
des Systems brechen, was meistens mit einem Magnetfeld gemacht wird. In einem Magnetfeld
spalten sich die Energieniveaus des Atoms auf, was dann zu dem Aufspalten und Polarisation
von Spektrallinien führt, wie schematisch in Abb. III.1 dargestellt ist. Dieses Phänomen, erstmal
in 1896 beobachtet, trägt den Namen des holländischen Physikers Pieter Zeeman, der für seine
Entdeckung mit dem Nobelpreis für Physik 1902 belohnt wurde.
Abb. III.1: Die Aufspaltung einer Spektrallinie in einem äußeren Magnetfeld.
Die Aufspaltung der Energieniveaus kann man nicht-relativistisch bestimmen. Dabei muss
man berücksichtigen, dass die Kreisbewegung des Elektrons um den Kern ein magnetisches Moment erzeugt, welches mit dem externen Magnetfeld wechselwirkt. Allerdings konnten diese
Überlegungen nicht alle experimentelle Beobachtungen erklären. Man sprach von einem “normalen” Zeeman-Effekt und einem “anomalen” Zeeman-Effekt, der nur unter Berücksichtigung
des vom elektronischen Drehimpuls verursachten magnetischen Moments nicht zu erklären war.
Eine Reihe von spannenden Experimenten in der Zwanzigerjahren des letzten Jahrhunderts,
gleichzeitig begleitet durch die weitere Entwicklung der Quantentheorie für relativistische Fälle,
haben das Problem des anomalen Zeeman-Effekts gelöst. Der Schlüssel zur Erklärung war der
Spin des Elektrons. 1922 haben Stern und Gerlach ein Experiment zur Bestimmung des atomaren magnetischen Moments durchgeführt. Dabei haben sie die Ablenkung von Silberatomen
in einem atomaren Strahl, der sich durch eines inhomogenen Magnetfeld bewegt, beobachtet.
Da man eine willkürliche Orientierung des atomaren magnetischen Moments erwartete, hätte
die Ablenkung symmetrisch um die ursprungliche Strahlachse sein sollen. Die Überraschung
war groß zu sehen, dass die magnetischen Momente der Silberatome nur zwei Orientierungen
haben, und die Ablenkung in dem inhomogenen Magnetfeld ein bestimmtes Muster formt, mit
zwei getrennten Linien symmetrisch um den Null-Punkt. Diese Quantisierung der magnetischen
Moment-Komponente in der Magnetfeldrichtung nennt man auch Raumquantisierung und stellt
die Quantisierung des Drehimpulses um eine Raumrichtung dar. Der Stern-Gerlach-Versuch und
seine Ergebnisse waren sehr verblüffend für die Physikgemeinde, die noch dabei war, die Quantenmechanik zu entwickeln. Zwar hatte Bohr die Drehimpuls Quantisierung schon eingeführt,
III.1. DIE SUCHE NACH EINER RELATIVISTISCHEN QUANTENMECHANIK
5
aber ein Drehimplus der keine ganze Zahl ist, hatte man noch nie gesehen.
Eine Erklärung kam 1925 von S. Goudsmit und G. E. Uhlenbeck, die versucht haben, die
rätselhaften Beobachtungen des anomalen Zeeman Effekts und des Stern-Gerlach-Versuchs in
einem Schlag zu erledigen. Die Lösung der Rätsel war die Einführung eines elektronischen
magnetischen Moments, welches einem Eigendrehimpuls, dem Spin, entspricht. Aus dem SternGerlach Experiment ergibt sich dann, dass der Spin des Elektrons s = 21 sein muss, während der
Bahndrehimpuls für die Silberatome null sein muss.
Währenddessen, 1924 machte Louis de Broglie sein berühmten Ansatz, dass der WelleTeilchen-Dualismus, der damals nur für Photonen bekannt war, ein Wesensmerkmal nicht nur der
Photonen sondern auch der Materie sei. Mit der Erkenntnis, dass alle Teilchen auch Welleneigenschaften besitzen, arbeitete de Broglie weiter an der Verbesserung des Bohr-Sommerfeldschen
Atommodells. Er ordnete jedem Elektron eine so genannte Materiewelle zu, die sich auf den
Bohrschen Bahnen ausbreitet. De Broglie zeigte auf diesem Weg die Beziehung zwischen der
Bahnstabilitt und dem Bahnumfang der Elektronen im Bohrschen Atommodell auf,
2πr = nλ ⇔ 2πr =
nh
.
p
(III.2)
Ein Elektron kann sich nur ohne Energieverlust um den Atomkern bewegen, wenn sein Bahnumfang ein ganzzahliges Vielfaches seiner Wellenlänge ist. Diese Ansätze lieferten wichtige Anregungen für Erwin Schrödinger, der noch im selben Jahr seine partielle Differentialgleichung, die
berühmte Schrödinger-Gleichung, aufstellte. Diese konnte das Verhalten der Elektronen in den
stationären Energiezuständen darstellen. Allerdings ist die Schrödinger-Gleichung, wegen seiner
unterschiedlichen Ordnungen der Zeit- und Raumableitungen nicht Lorentz-kovariant, also nicht
relativistisch.
Ein Versuch, die Schrödinger-Gleichung und den Spin des Elektrons zu vereinbaren führte
1927 zur Pauli-Gleichung,
1
2
~ + eΦ |ψi = i~ ∂ |ψi ,
(~σ · (~
p − q A))
2m
∂t
(III.3)
die selbst wenn immer noch nicht-relativistisch, beinhaltet schon den 12 -Elektronspin. Die
entsprechende Spinoren-Darstellung kommt über die Pauli-Matrizen ~σ , einen Satz von hermitischen und unitären 2 × 2 Matrizen,
σx =
σy =
σz =
0 1
!
,
1 0
0 −i
i
0
1
0
!
0 −1
,
!
.
(III.4)
Die Pauli-Gleichung geeignet sich zur Beschreibung der noch nicht relativistischen atomaren
Systeme wo die Elektronengeschwidigkeit noch viel kleiner als die Lichtgeschwindigkeit ist.
In dem Bemühen, eine relativistische Quantenmechanik zu formulieren, hat man zunächst
versucht, mittels des Korrespondenzprinzips eine relativistische Wellengleichung aufzustellen,
die die Schrödinger-Gleichung ersetzen sollte. Die erste derartige Gleichung war die von
6
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Schrödinger [Schr1926b], Gordon [Gord1926] und Klein [Klei1927] aufgestellte skalare Wellengleichung zweiter Ordnung, die nun den Namen Klein-Gordon-Gleichung trägt. Aus der EnergieImpuls-Beziehung
p
E = p2 c2 + m2 c4 ,
(III.5)
durch Ersetzung von klassischen Größen durch Operatoren,
E → i~
p~ →
∂
,
∂t
~
∇,
i
(III.6)
erhielt man eine Wellengleichung,
i~
p
∂
ψ = −~2 c2 ∇2 + m2 c4 ψ .
∂t
(III.7)
Eine offensichtliche Schwierigkeit dieser Gleichung besteht in der Wurzel aus der räumlichen
Ableitung, deren Entwicklung auf unendlich hohe Ableitungen führt. Deswegen geht man
stattdessen von der quadrierten Relation
E 2 = p2 c2 + m2 c4 ,
(III.8)
aus, was dann
∂2
ψ = (−~2 c2 ∇2 + m2 c4 )ψ .
∂t2
Die noch kompaktere, und offensichtlich kovariante Form
mc 2 ∂µ ∂ µ +
ψ = 0,
~
− ~2
(III.9)
(III.10)
ist under dem Namen Klein-Gordon-Gleichung bekannt. Hier ist xµ der raum-zeitliche Ortsvektor xµ = (ict, ~r) und der Kovariante Vektor ∂µ = ∂x∂ µ ist die vierdimensionale Verallgemeinerung
des Gradientenvektors. Es wurde die Einsteinische Summenkonvention benutzt, und über doppelt auftretende Indizes summiert. Wenn man aber eine Kontinuitätsgleichung aus der KleinGordon-Gleichung herleiten möchte, stoßt man auf negative Warscheinlichkeitsdichten, die unphysikalisch sind. Außerdem merkte man, dass die Lösungen der Klein-Gordon-Gleichung sowohl
positive als auch negative Energien haben, und die Energie nach unten nicht beschränkt ist. Die
Gleichung wurde deshalb verworfen, da sie ihr primäres Ziel, eine relativistische Theorie für das
Elektron zu entwickelt, verfehlt hatte. Die richtige relativistische Theorie fürs Elektron wurde
von Paul A. M. Dirac 1928 entwickelt [Dira1928], der seine Überlegungen mit ganz ähnlich auf
dem Korrespondenzprinzip und der Energie-Impuls-Beziehnung bezog.
III.2
Die Dirac-Gleichung für Wasserstoff-ähnliche Systeme
Die Klein-Gordon-Gleichung hat sich als ungeeignet für die Berechnung der Warscheinlichkeitsamplitude erwiesen. Dirac, auf seiner Suche nach einer Wellengleichung für die Warscheinlichkeitsamplitude, war der Meinung, dass man eine Gleichung braucht, die erste Ordnung in
der Raum- und Zeitableitung ist. Dafür musste man mit der Energie-Impuls-Beziehnung (III.5)
anfangen, was große Schwierigkeiten wegen der Wurzel stellte. Was bedeutet eine Wurzel von
Operatoren? Soll man die in einer unendlichen Reihe entwickeln und dann versuchen, die dabei
III.2. DIE DIRAC-GLEICHUNG FÜR WASSERSTOFF-ÄHNLICHE SYSTEME
7
entstandene sehr hessliche Gleichung iterativ zu lösen? Dirac hatte eine vielversprechende Idee,
wie man das Wurzel-Problem entkommen kann. Er merkte, dass
∇2 −
1 ∂2
i
i
= (αx ∂x + αy ∂y + αz ∂z + β∂t )(αx ∂x + αy ∂y + αz ∂z + β∂t ) ,
c2 ∂t2
c
c
(III.11)
unter der Voraussetzung, dass die ganze Mischterme ∂x ∂y verschwinden, die Lösung seines Problems liefern würde. Dabei müssen die Koeffizienten die folgenden Bedingungen erfüllen,
αi αj + αj αi = 0
mit
i 6= j, i, j = x, y, z
αi β = 0
αi2 = β 2 = 1
(III.12)
Für Dirac, der zu der Zeit gerade mit der von Born und Heisenberg entwickelte Matrix-Mechanik
beschäftigt war, wurde sofort klar, dass solche Bedingungen nur von Matrizen erfüllt werden
können. Die unbekannten Koeffizienten αi und β waren also Matrizen, und es wurde gezeigt,
dass sie mindestens 4 × 4 Matrizen sein müssen, um die Bedingungen (III.12) zu erfüllen. Die
gesuchte Wellenfunktion hat also 4 Komponenten, und nicht nur zwei, wie man es von der
Pauli-Gleichung kannte. Die Dirac-Gleichung für ein freies Elektron lautet dann
i~
∂
ψ = (c~
α · p~ + βmc2 )ψ .
∂t
(III.13)
Die Matrizen α
~ = (αx , αy , αz ) und β sind 4 × 4 Matrizen, die Antikommutator-Relationen
erfüllen (III.12), was bedeutet, dass die Wellenfunktion 4 Komponenten hat,


ψ (~r, t)
 1

ψ (~r, t)
2


ψ=
(III.14)

ψ3 (~r, t)


ψ4 (~r, t)
Eine Mögliche Darstellung der Matrizen ist


1 0 0
0


0 1 0
0


β = 
=
0 0 −1 0 


0 0 0 −1
!
0 ~σ
α
~ =
,
~σ 0
I
0
0 −I
!
,
(III.15)
wo I die 2 × 2 Einheitsmatrix ist, und ~σ die Pauli Matrizen (III.4). Man kommt also zu den
von Pauli für die Beschreibung des Spins eingeführte Matrizen zurück. Die Dirac-Gleichung, die
ganz allgeimein aus der Energie-Impuls-Beziehung als relativistische Wellengleichung abgeleitet
worden wurde, konnte die Existenz des 21 -Elektronspins bestätigen. Deswegen ist der Spin der
Teilchen als eine strikt relativistische Eigenschaft betrachtet.
Die Dirac-Gleichung (III.13) in Verbindung mit den Matrizen (III.15) wird Standarddarstellung der Dirac-Gleichung genannt. Man bezeichnet die Wellenfunktion (III.14) als Viererspinor
oder manchmal Bispinor, insbesondere dann, wenn ψ durch zwei Zweierspinoren dargestellt wird.
8
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Die Auswahl der Matrizen (III.15) ist nicht eindeutig, es lässt sich aber zeigen, dass eine beliebige
Auswahl für α
~ und β mit den Eingeschaften (III.12) dieselbe physikalische Ergebnisse liefert.
Die Dirac-Gleichung besitzt ebenso wie die Klein-Gordon-Gleichung Lösungen mit negatives Energie, so dass für jeden Quantenzustand mit positiver Energie E gibt es einen korrespondierenden Zustand mit der Energie −E. Der erlaubte Energiebereich für Kontinuumzusände, gegeben
durch die Energieeigenwerte für ein freies Elektron ist E < −mc2 und E > mc2 . Ein Elektron
mit positiver Energie könnte durch Emission von Photonen Übergänge in beliebig tief liegende
Zustände mit negativer durchführen und dabei unendlich viel Energie abstrahlen. Um dies zu
verhindern, postulierte Dirac 1930 [Dira1930] dass die Zustände mit negativer Energie alle besetzt sind. Diese unendliche Menge von Elektronen, die alle Zustände mit negativer Energie
besetzen, wurden Dirac Sea genannt, das Dirac’sche Meer also. Allerdings ist es auf Deutsch
unter Dirac-See bekannt, was nicht der genaue Übersetzung entspricht. Löcher in dem Dirac-See
stellen Teilchen mit engegengesetzter Ladung (Antiteilchen) dar. Das Positron, das Antiteilchen
des Elektrons, wurde das erste Mal von Carl Anderson 1932 experimentell gesehen. Das DiracSee Bild gibt eine anschauliche Erklärung was passiert, wenn ein Positron und ein Elektron sich
treffen: das Elektron kann einen Übergang zu dem freien Zustand von negativer Energie machen
unter Emission von Strahlung. Dabei verschwinden sowohl das Elektron, als auch das Loch, also
das Positron, was under Annihilation bekannt ist. Die Dirac-See Interpretation, die ursprunglich
von Dirac eingeführt wurde, ist heutzutage veraltet. Quantenfeldhteorie beschreibt das Positron
als ein reeles Teilchen, nicht als Loch, und damit muss man kein Vakuum haben, welches schon
eine unendliche Menge von Teilchen beinhaltet.
III.2.1
Kovariante Form der Dirac-Gleichung
Die Dirac-Gleichung (III.13) kann auch in kovarianter Form geschrieben werden, indem man
versucht, dass zeitliche und räumliche Ableitungen mit Matrizen mit ähnlichen algebraischen
Eigenschaften multipiziert werden. Dafür kann man die Dirac-Gleichung mit −iβ/c von links
multiplizieren,
~∂
(−iβ~
α · p~ − imc − β
)ψ = 0 .
(III.16)
c ∂t
Nun definieren wir neue Dirac-Matrizen,
γ µ = (β, −iβ~
α)
(III.17)
womit man die Dirac-Gleichung dann die Gestalt annimmt
mc
(γ µ ∂µ +
)ψ = 0 .
(III.18)
~
Dabei wurde die Einsteinische Summenkonvention benutzt, und über doppelt auftretende Indizes
summiert. Die neue Dirac-Matrizen, die γ-Matrizen haben die Eingenschaft
γ ν γ µ + γ µ γ ν = 2δ µν I .
In der speziellen Darstellung (III.15) haben die γ-Matrizen die Form
!
!
I 0
0 σi
0
i
γ =
, γ =
.
0 −I
−σi 0
(III.19)
(III.20)
Eine äquivalente Darstellung der γ-Matrizen, die ebensfalls die algebraischen Relationen (III.19)
erfüllt, erhält man duch γ → M γM −1 , wo M eine beliebige nichtsinguläre Matrix ist. Andere in
der Teilchenphysik gebräuchliche Darstellungen sind die Majorana-Darstellung und die chirale
Darstellung.
III.2. DIE DIRAC-GLEICHUNG FÜR WASSERSTOFF-ÄHNLICHE SYSTEME
III.2.2
9
Die Dirac-Gleichung für ein Zentralfeld
Die bis jetzt erhaltene Dirac-Gleichung beschreibt ein freies Elektron. Man kann jederzeit
dazu ein elektromagnetisches Feld ankoppeln durch die übliche Ersetzung pµ → pµ − eAµ , wo
~
Aµ = ( iΦ
c , A) der Potential Vierervektor ist, der sowohl das skalare Potential Φ als auch das
~ beinhaltet. Damit erhält man die Dirac-Gleichung
Vektorpotential A
(γ µ (pµ − eAµ ) − imc)ψ = 0 .
(III.21)
Für ein skalares Zentralfeld haben wir Aµ = δµ0 A0 (r) = δµ0 iΦ(r)
c , und im Fall vom CoulombZe
Potential, Φ(r) = 4π
.
Die
Dirac-Gleichung
für
ein
Wasserstoff-ähnliches
System ist gegeben
0r
durch (diesmal nicht in der expliziten kovarianten Form)
(c~
α · p~ + mc2 β + eΦ(r))ψ = i~
∂ψ
.
∂t
(III.22)
Angenommen, dass die Wellenfunktion die bekannte Zeitabhängigkeit hat,
E
ψ(~r, t) = Ψ(~r) e−i ~ t ,
(III.23)
(c~
α · p~ + mc2 β + eΦ(r))Ψ = EΨ .
(III.24)
erhalten wir die Gleichung
Wir machen uns jetzt auf der Suche nach der Lösungen dieser Gleichung. Wie man von der Quantenmechanik schon weiss, Operatoren, die untereinander tauschen, haben auch einen gemeinsamen Satz von Eigenvektoren. Um die Eingenvektoren des Dirac-Hamiltonian-Operators
HD = c~
α · p~ + mc2 β + eΦ(r)
(III.25)
zu finden schauen wir dann zuerst nach denjenigen Operatoren, die mit ihm vertauschen. Von
der Lösung der Schrödinger-Gleichung können wir uns erinnern, dass der Bahndrehimpuls ein
solcher Operator war, der mit dem Zentralfeld-Hamiltonoperator vertauschte. Allerdings ist die
Situation bei der Dirac-Gleichung komplizierter, da wir mehrere Drehimpulse haben, z.B. der
Spin. Das Elektron hat jetzt einen Spin, der mit dem Spin-Operator
!
~
σ
0
~
~=
S
,
(III.26)
2 0 ~σ
verbunden ist. Der Spin ist ein Drehimpuls, bzw. seine Komponente erfüllen die Vertauschungsrelationen [Si , Sj ] = i~ijk Sk , wo ijk der Levi-Civita Tensor ist und i, j, k = 1, 2, 3.
Man kann sofort das Quadrat des Spin-Operators berechnen,
!
I
0
3
~ 2 = ~2
.
(III.27)
S
4
0 I
~ + S.
~ Der
Die Kopplung vom Spin und Bahndrehimpuls ergibt den Gesamtdrehimpuls J~ = L
Bahndrehimpuls für unser System mit Vierer-Wellenfunktion hat die Darstellung
!
I
0
~ = ~r × p~
L
.
(III.28)
0 I
10
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Der Gesamtdrehimpuls ist dann
J~ =
~
σ
2~
+ ~r × p~I
!
0
~
σ
2~
0
,
+ ~r × p~I
(III.29)
~ S
~ 2] =
und erfüllt die Vertauschungsrelationen [Ji , Jj ] = i~ijk Jk , [Ji , J~2 ] = 0, mit i = 1, 2, 3, [J,
2
2
2
~ L
~ ] = 0. Man kann zeigen, dass die folgenden Operatoren vertauschen: Jz , J~ , HD , S
~ und
[J,
noch dazu
K=β
2 ~ ~
S·L+1
~2
=β
1 ~2 ~ 2 ~ 2
(J − L − S ) + 1
~2
=β
1 ~2 ~ 2
1
(J − L ) +
2
~
4
.
(III.30)
Dabei ist K der Spin-Bahn-Operator, der bei dem Umschreiben der Dirac-Gleichung auf
Kugelkoordinaten auftaucht. Für das Problem des relativistischen Elektrons in einem Zentralfeld ist es vorteilhaft, genau wie bei der Schrödinger-Gleichung für das Wasserstoff-Atom,
die Kugenkoordinaten zu benutzen, womit die Dirac-Gleichung lautet
~ ∂
1
~β
2
cαr
+
K + mc β + eΦ(r) Ψ = EΨ .
−
(III.31)
i ∂r r
ir
Hier ist die radiale Komponente der α
~ -Matrix
αr =
0
σr
σr
0
!
,
(III.32)
mit
σr = σx cos ϕ sin θ + σy sin ϕ sin θ + σz cos θ ,
(III.33)
oder in Matrixform
σr =
cos θ
sin θe−iϕ
sin θeiϕ
− cos θ
!
.
(III.34)
~ 2 und K? Dafür untersuchen wir erstmal einzeln
Wer sind jetzt die Eigenfunktionen zu Jz , J~2 , S
das Eigenwertproblem für jeden Operator.
Eigenfunktionen von Jz und J~2 : Von den zwei-komponentigen Eigenfunktionen erwarten
wir, wie bei jedem Drehimpuls, dass die Operatoren Jz und J~2 , wo J~ in (III.29) definiert ist,
die folgenden Eigenwert-Gleichungen haben,
Jz Ψjm = m~Ψjm ,
J~2 Ψjm = j(j + 1)~2 Ψjm .
(III.35)
~ und L
~ entsteht, sollen die Eigenfunktionen Ψjm die Form haben
Da J~ von der Kopplung von S
Ψjm =
l
X
1/2
X
(l m1
m1 =−l m2 =−1/2
1
m2 |j m)Ylm1 (θ, ϕ)χm2 ,
2
(III.36)
mit den Spinoren
χ1/2 =
1
0
!
,
χ−1/2 =
!
0
1
.
(III.37)
III.2. DIE DIRAC-GLEICHUNG FÜR WASSERSTOFF-ÄHNLICHE SYSTEME
11
Hier bezeichnen (l m1 12 m2 |j m) die Clebsch-Gordan Koeffizienten, die uns von der
Kopplung von Drehimpulsen in der Quantenmechanik bekannt sind, und Ylm sind die
Kugelflächenfunktionen. Man kann dann die Eigenfunktionen von Jz und J~2 explizit für die
zwei mögliche Beziehungen zwischen l und j schreiben,
• l = j − 12 , also Spin und Bahndrehimpuls parallel,
Ψl=j− 1 ,jm
2
1
=√
2l + 1
r
1
l + m + Ylm− 1 (θ, ϕ)χ 1 +
2
2
2
r
!
1
l − m + Ylm+ 1 (θ, ϕ)χ− 1 .
2
2
2
(III.38)
• l = j + 12 , also Spin und Bahndrehimpuls antiparallel,
Ψl=j+ 1 ,jm
2
1
=√
2l + 1
!
1
l + m + Ylm+ 1 (θ, ϕ)χ− 1 .
2
2
2
(III.39)
r
r
1
− l − m + Ylm− 1 (θ, ϕ)χ 1 +
2
2
2
Eigenfunktionen von K: Sei es k =
gegeben durch
2 ~
S
~2
K=β
~ +1 =
·L
k 0
!
=
0 k
1 ~2
(J
~2
k
~ 2 ) + 1 . Der Operator K ist dann
−L
4
0
!
0 −k
.
(III.40)
Wir suchen jetzt die Eigenfunktionen von k, so dass kΨ = −κΨ. Der Eigenwert von k ist also
−κ. Lass uns nachprüfen, wie die Eigenfunktionen von Jz und J~2 die Eigenwert-Gleichung von
k erfüllen. Es lässt sich leicht zeigen, dass
1
1
1
1
kΨl=j− 1 ,jm = (j(j + 1) − (j − )(j + ) + )Ψl=j− 1 ,jm = (j + )Ψl=j− 1 ,jm ,
2
2
2
2
2
4
2
1
3
1
1
kΨl=j+ 1 ,jm = (j(j + 1) − (j + )(j + ) + )Ψl=j+ 1 ,jm = −(j + )Ψl=j+ 1 ,jm .
2
2
2
2
2
4
2
(III.41)
Die Eigenfunktionen von Jz und J~2 sind also auch Eigenfunktionen von k, zu den Eigenwerten
κ = −(j + 21 ), bzw. κ = (j + 21 ), also κ = ±1, ±2, ±3, . . .. Wir können jetzt die Eigenfunktionen
statt mit j und l nur mit κ indexieren, Ψκm . Es unterscheiden sich wieder die zwei Fälle für die
Orientierung der Spin- und Bahndrehimpulse: sind Spin- und Bahndrehimpuls parallel, bzw. ist
κ negativ, haben wir
κ = −|κ|
j = |κ| −
1
,
2
l = |κ| − 1 .
(III.42)
Ein positives κ zeigt dagegen, dass die Spin- und Bahndrehimpulse antiparallel ist, und
κ = |κ|
j = |κ| −
1
,
2
l = |κ| .
(III.43)
Einige Beispiele von Quantezahlen für die Dirac-Energieniveaus im Wasserstoffatom mit den
entsprechenden Quantenzahlen sind in der Tabelle III.1 dargestellt.
12
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Tabelle III.1: Relativistische Quantenzahlen für die Dirac-Energieniveaus: Spin-BahnQuantenzahl κ, Gesamtdrehimpulsquantenzahl j, Bahndrehimpulsquantenzahlen l1 und l2 für
die obere, bzw. untere Spinor-Komponente und die entsprechenden spektroskopischen ZustandBezeichnungen.
κ
j
l1
l2
Bezeichnung
–1
1/2
0
1
s1/2
+1
1/2
1
0
p1/2
–2
3/2
1
2
p3/2
+2
3/2
2
1
d3/2
–3
5/2
2
3
d5/2
+3
5/2
3
2
f5/2
–4
7/2
3
4
f7/2
+4
7/2
4
3
g7/2
~ 2 : Bis jetzt haben wir die zwei-komponentige
Eigenfunktionen von K, Jz , J~2 und S
Eigenfunktionen von den Operatoren K, Jz und J~2 gefunden. Mit ihnen können wir jetzt die
~ 2 aufstellen. Sei es
vier-komponentige Eigenfunktionen von K, Jz , J~2 und S
!
!
Ψκm
0
1
2
Ψκm =
, Ψκm =
.
(III.44)
0
Ψ−κm
Wir prüfen jetzt nach, ob Ψ1κm und Ψ2κm Eigenfunktionen von unseren Operatoren sind, und zu
welchen Eigenwerten. Man kann leicht zeigen, dass
1,2
Jz Ψ1,2
κm = m~Ψκm ,
1
1
1,2
2 1,2
~
|κ| +
~2 Ψκm
,
J Ψκm =
|κ| −
2
2
3 2 1,2
~ 2 Ψ1,2
S
~ Ψκm
κm =
4
!
!
!
k 0
Ψκm
kΨκm
1
KΨκm =
=
= −κΨ1κm ,
0 −k
0
0
!
!
!
k
0
0
0
KΨ2κm =
=
= −κΨ2κm .
0 −k
Ψ−κm
−kΨ−κm
(III.45)
Die zwei Eigenfunktionen Ψ1κm und Ψ2κm haben für alle betrachtete Operatoren dieselben Eigenwerte. Mit Hilfe diesen Funktionen kann man also die Lösung der Dirac-Gleichung für das
Zentralfeld finden.
~2
Bemerkung: Die Funktionen Ψ1,2
κm sind auch Eigenfunktionen von dem Bahndrehimpuls L ,
aber mit verschiedenen Eigenwerten. Für κ > 0,
~ 2 Ψ1κm = l1 (l1 + 1)Ψ1κm = κ(κ + 1)~2 Ψ1κm ,
L
~ 2 Ψ2κm = l2 (l2 + 1)Ψ2κm = (κ − 1)κ~2 Ψ2κm .
L
(III.46)
III.2. DIE DIRAC-GLEICHUNG FÜR WASSERSTOFF-ÄHNLICHE SYSTEME
13
Für Ψ1κm ist also für κ > 0 l1 = κ, während l2 = κ − 1. Man kann zeigen, dass die verschiedene
Eigenwerte für die Eigenfunktionen Ψ1,2
κm die folgende Beziehung zu κ haben
(
l1 =
κ
if κ > 0 ,
|κ| − 1
if κ < 0 ,
(
l2 =
κ − 1 if κ > 0 ,
|κ|
(III.47)
if κ < 0 .
Es kommt oft vor, dass die relativistische Wellenfunktionen mit der Gesamtdrehimpulsquantenzahl j und der Bahndrehimpulsquantenzahl der oberen Komponente l1 bezeichnet wird.
Damit gibt es eine Verbindung zu der Notation für nichtrelativistische Wellenfunktionen. Die
entsprechende Werte von l1 und l2 für verschiedene atomare Orbitale sind zusammen mit den j
und κ Werte in der Tabelle III.1 dargestellt.
Für die Eigenfunktionen des Dirac-Hamiltonoperators machen wir nun den Ansatz,
Ψ=
g(r)Ψ1κm
+
if (r)Ψ2κm
=
!
g(r)Ψκm
if (r)Ψ−κm
.
(III.48)
wo jetzt g(r) und f (r) die Radialfunktionen der oberen und unteren Komponente sind, auch
als große bzw. kleine Komponente des Dirac-Spinors bezeichnet. Mit Hilfe diesem Ansatz kann
man jetzt die Dirac-Gleichung fürs Zentralfeld (III.24) in zwei Differenzialgleichungen für die
Radialfunktionen g(r) und f (r) schreiben. Dabei benutzen wir die Auswirkung der αr Matrix
auf den Dirac-Spinor [Rose1971],
αr Ψ =
−if (r)Ψκm
!
,
−g(r)Ψ−κm
(III.49)
und auch dass
αr βKΨ = αr β(−κ)Ψ = −καr
g(r)Ψκm
−if (r)Ψ−κm
!
=
−if (r)Ψκm
g(r)Ψ−κm
!
.
(III.50)
Damit erhält man die beiden radialen Gleichungen wenn obere und untere Komponente getrennt
geschrieben werden:
df
κ−1
1
−
f − (mc2 + eΦ(r) − E)g = 0 ,
dr
r
~c
1
dg κ + 1
+
g − (mc2 − eΦ(r) + E)f = 0 .
dr
r
~c
(III.51)
Wir werden die Lösung dieser Gleichungen nicht explizit berechnen, da dies ausserhalb der
Reichweite dieser Vorlesung ist. Die Radialefunktionen sind von konfluenten hypergeometrischen
Funktionen bestimmt. Eine ausführliche Behandlung findet man in Ref. [Land1986]. Demnächst
betrachten wir nur qualitativ die Asymptotik der Wellenfunktion. Für gebundene Zustände
erwartet man Radialfunktionen in der Form
g(r) =
a1 −λr
e
,
r
f (r) =
a2 −λr
e
.
r
(III.52)
14
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
In dem asymptotischen Fall, wenn r → ∞ lassen sich die Radialgleichungen unter Vernachlässigung der r12 Terme wie folgt schreiben
1
(mc2 + E)a2 = 0 ,
c~
1
−λa2 − (mc2 − E)a1 = 0 .
c~
− λa1 −
(III.53)
Hat dieses Gleichungssystem in a1 und a2 auch nichttriviale Lösungen, muss die Determinante
des Systems gleich Null sein,
1
2 + E) (mc
λ
~c
(III.54)
1
= 0,
(mc2 − E)
λ
~c
was dazu führt, dass
mc2
λ=±
~c
s
1−
E2
.
(mc2 )2
(III.55)
Damit g(r) und f (r) gebundene Zustände beschreiben, muss λ reel und positiv sein, was als
Bedingung für die Energie auswirkt,
− mc2 < E < mc2 .
(III.56)
Die gebundene Zustände sind also in dem Energieinterval (−mc2 , mc2 ) zu finden, im Gegensatz
zu den Kontinuumzustände, die sich nur ausserhalb dieses Intervals befinden, wie schematisch
in Abb. III.2 dargestellt.
Abb. III.2: Das Dirac-Spektrum für gebundene und Kontinuum-Zustände
Mit der Notation = E/(mc2 ), erhalten die Radialwellenfunktionen den Ausdruck
√
e−λr
g(r) = A 1 + ,
r
√
e−λr
f (r) = −A 1 − .
r
(III.57)
III.2. DIE DIRAC-GLEICHUNG FÜR WASSERSTOFF-ÄHNLICHE SYSTEME
15
Ein Vergleich zwischen g(r) und f (r) zeigt sofort wieso sich die zwei Komponenten der DiracWellenfunktion die “große” und die “kleine” Komponente nennen. Das Verhältnis
r
g(r)
1+
=−
f (r)
1−
(III.58)
wird für ≈ 1 sehr groß, und damit die obere Komponente des Dirac-Spinors viel größer als
die untere Komponente, |g| |f |. Ein Beispiel für radialen Wellenfunktionen für die 2s1/2 und
2p3/2 in Wasserstoff-ähnlichem Uran (Z = 92) sind in Abb. III.3 zu sehen. Die gebundenen
Wellenfunktionen sind mit den schnell-oszillierenden Wellenfunktionen für ein freies Elektron in
der Nähe eines Uran-Kerns verglichen.
40
5
gκ(r)
fκ(r)
gκ(r)
fκ(r)
4
Bound rwf (au)
Bound rwf (au)
30
20
10
0
-10
3
2
1
0
(a)
(b)
-20
-1
0
1
2
3
4
5
0
1
2
Continuum rwf (au)
r (au)
3
4
5
r (au)
14
12
10
8
6
4
2
0
-2
-4
-6
gκ(r)
fκ(r)
(c)
0
1
2
3
4
5
r (au)
Abb. III.3: Relativistische Elektronenwellenfunktionen: die radiale Wellenfunktionen gκ (r) und
fκ (r) für das 2s1/2 Orbital (a) und das 2p3/2 Orbital in Wasserstoff-ähnlichem Uran (Z = 92).
(c) Radiale Wellenfunktionen gκ (r) und fκ (r) für ein freies Elektron mit Energie E = 15.27 keV
und κ = 2 in der Nähe eines He-artigen Urans. Es wurden atomaren Einheiten (au) benutzt.
III.2.3
Diskretes Spektrum
Sowohl die diskrete Eigenwerte als auch die dazugehörigen Eigenfunktionen lassen sich analytisch
bestimmen. Die Zustände sind mit den Quantenzahlen nljm bezeichnet, wobei n die Hauptquantenzahl ist, n = 1, 2, 3, . . . und l ist der l-Wert der großen Komponente, also l1 in (III.47),
analog zu der nicht-relativistische Bezeichnungsweise. Es gilt l < n, so dass l = 0, 1, . . . , n − 1.
Bezeichnet werden die Zustände mit l = 0, 1, 2, 3, 4, . . . durch die Kleinbuchstaben s (sharp), p
(principal), d (diffuse), f (fundamental), g, h, . . . . Die weitere Indices m und j sind die zu dem
16
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Gesamtdrehimpuls zugehörigen Quantenzahlen, mit m = −j, −j + 1, . . . , j. Die Energieeigenwerte sind gegeben durch
Enj = mc2 r
1+
1
.
(III.59)
2
(αZ)
√
n−(j+1/2)+
(j+1/2)2 −(αZ)2
und sind in l und m entartet. Hier bezeichnet α die Feinstrukturkonstante, α = 1/137.035. Für
den Fall, dass αZ 1, wie z.B. bei Wasserstoff, kann man die Energien in (III.59) nach αZ
entwickeln, mit dem Ergebnis
Enj
(αZ)2 (αZ)4
1
3
− ... .
= mc 1 −
−
−
2n2
2n3
j + 1/2 4n
2
(III.60)
Der erste Term in der obigen Gleichung, mc2 , entspricht der Ruhenergie des Elektrons. In dem
zweiten Term kann man den Eigenwert der Schrödinger-Gleichung erkennen, also die nichtrelativistische Bindungsenergie. Für n = 1 haben wir
|E1 | =
(αZ)2 2
mc = 13, 6 Z 2 eV ,
2
(III.61)
was für das Wasserstoffatom den bekannten Wert 13,6 eV liefert. Der dritte Term in (III.60) erhebt für die Dirac-Gleichung Eigenwerte im Vergleich zu den Schrödinger-Gleichung Eigenwerten
teilweise die Entartung. Ein nicht-relativistischer nur von der Hauptquantenzahl abhängiger
Energie-Eigenwert En spaltet sich in n Niveaus laut Dirac-Theorie, für jeden Gesamtdrehimpulsquantenzahl j = 1/2, 3/2, . . . , n − 1/2. Diese Aufspaltung ist under dem Namen Feinstruktur
bekannt. Die Konstante α ' 1/137, die die Skala dieser Aufspaltung kontroliert, wird deswegen
Feinstruktur-Konstante gennant. Die Feinstrukturaufspaltung für eine bestimmte Hauptquantenzahl n mit jmin = 1/2 und jmax = n − 1/2 ist gegeben durch
∆EF n = En,jmax − Enjmin = |En |(αZ)2
n−1
.
n2
(III.62)
Die typische Werte für die Feinstrukturaufspaltung für die ersten drei atomaren Schalen sind in
der Tabelle III.2 gegeben. Abb. III.4 zeigt die Schrödinger und die Dirac Energie-Eigenwerte
für das Wasserstoffatom.
In der Dirac-Theorie haben zwei Zustände mit derselben Hauptquantenzahl n und Gesamtdrehimpulsquantenzahl j, aber mit verschiedener Bahndrehimpulsquantenzahl l = j ± 1/2
dieselbe Energie. Die Parität der Zustände ist aber von (−1)l gegeben, also haben sie unterschiedliche Paritäten. Die Entartung der Energie-Niveaus nach l wird von kleinen quantenelektrodynamischen Effekten, auch Strahlkorrekturen genannt, aufgehoben. Die Strahlkorrekturen
sind für die zusätzliche Energie-Verschiebung zwischen den 2s1/2 und 2p1/2 Niveaus, die LambVerschiebung, verantwortlich.
Bemerkung: Die Spektrallinien, die bei Übergängen zwischen Feinstruktur-Niveaus entstehen, bilden ein Multiplett von Linien. Da die Emission von Strahlung, bzw. der Dipol-Moment
nicht vom Spin abhängt, sind die Auswahlregel für Elektrisch-Dipol Übergänge immer noch dieselben, also ∆l = ±1 und ∆j = ±1. Ein Schema mit den möglichen Übergängen zwischen den
n = 3 und n = 2 atomaren Schalen zusammen mit den beobachteten Spektrallinien sind in Abb.
III.5 dargestellt.
III.3. ÜBERGANG ZU SCHRÖDINGER-ÄHNLICHEN GLEICHUNGEN
17
Tabelle III.2: Relativistische Quantenzahlen und Energien für die Dirac-Energieniveaus: Hauptquantenzahl n, Spin-Bahn-Quantenzahl κ, Gesamtdrehimpulsquantenzahl j, Bahndrehimpulsquantenzahl für die große Komponente l1 , die Schrödinger-Energie in |E1 |-Einheiten und die
entsprechenden Feinstruktur-Korrekturen.
l1
Spektr. Bez.
En /|E1 |
EF nj /((αZ)2 |E1 |)
–1
1/2
0
1s1/2
-1
–2
3/2
1
2p3/2
- 14
–1
1/2
0
2s1/2
- 14
+1
1/2
1
2p1/2
- 14
–3
5/2
2
3d5/2
- 19
–2
3/2
1
3p3/2
- 19
+2
3/2
2
3d3/2
- 19
–1
1/2
0
3s1/2
- 19
+1
1/2
1
3p1/2
- 19
1
4
1
- 64
5
- 64
5
- 64
1
- 324
3
- 324
3
- 324
9
- 324
9
- 324
κ
1
2
3
III.3
j
n
-
Übergang von der Dirac-Gleichung zu Schrödingerähnlichen Gleichungen
Die Dirac-Gleichung ist linear in der Zeit- und Koordinaten-Ableitung. Wir versuchen jetzt von
der Dirac-Gleichung zu einer Gleichung zu kommen, die der Schrödinger-Gleichung ähnlich ist,
also zweiter Ordnung in die Raum-Ableitung ist. Dafür starten wir von der kovarianten Form
(γ µ (pµ − eAµ ) − imc)ψ = 0 ,
(III.63)
und multiplizieren von links mit dem Faktor
0
(γ µ (pµ0 − eAµ0 ) + imc) .
(III.64)
Dies ergibt
0 = ((pµ − eAµ )2 + m2 c2 )ψ −
~e µ µ0
γ γ Fµµ0 ψ ,
2i
(III.65)
wo wir mit die folgende Notation benutzt haben,
Fµν =
∂
∂
Aν −
Aµ .
∂xµ
∂xν
(III.66)
Der erste Teil der Gleichung (III.65) enspricht der Klein-Gordon-Gleichung, währen der zweite
Term für die Wechselwirkung zwischen dem Spin und dem elektromagnetischen Feld steht. Man
definiert dabei ein Dirac’sches Moment,
!
~σ 0 ~ ~e
~e
γµ γν Fµν = ~e
B+
2i
ic
0 ~σ
0 ~σ
~σ
0
!
~,
E
(III.67)
18
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Abb. III.4: Feinstruktur für das Wasserstoff-Atom. Die nicht-relativistische Werte sind links
gezeigt (a), mit der Feinstruktur-Aufspaltung rechts (b). Die benutzte Abbildung-Skala ist für
jedes Niveau aus Sichtbarkeitsgründen eine andere.
welches ein elektrisches und magnetisches Dipolmoment zugleich ist. Hier wurde wieder die
Einsteinische Summenskonvention benutzt. Unter der Annahme, dass die Wellenfunktion die
übliche Zeitabhängigkeit hat,
ψ = e−
imc2 t
~
ψ̃ ,
erhält man nach einfachen Schritten
"
∂
~ 2
(i~ ∂t
− eΦ)2
∂ ψ̃
(p − eA)
~e
i~
=
+ eΦ −
−
2
∂t
2m
2mc
2m
(III.68)
#
i~e
~+
~ ψ̃ .
B
α
~ ·E
2mc
0 ~σ
~σ
0
!
(III.69)
Das ist eine exakte Gleichung die aus der Dirac-Gleichung hergeleitet wurde, nämlich die Pauli~ mischt die oberen und unteren
Gleichung mit relativistischen Korrekturen. Der Term ∼ α
~ ·E
2
i~e
~ vernachlässigt werden, erhält man die PauliKomponenten. Wenn (i~∂/∂t−eΦ)
und 2mc
α
~ ·E
2mc2
Gleichung für die große Komponente. In erster Ordnung in v/c ist die Dirac-Gleichung der nur
zwei-komponentigen Pauli-Gleichung äquivalent. Um von dem 4-komponentigen Dirac-Spinor
auf eine 2-komponentige Wellenfunktion zu kommen, kann man versuchen, die kleine Komponente nährungsweise zu eliminieren. Dafür schreibt man die Wellenfunktion in (III.69) als
!
χ̃
ψ̃ =
.
(III.70)
ϕ̃
Aus der Pauli-Gleichung mit relativistischen Korrekturen (III.69) kann man eine Beziehung
zwischen den zwei Komponenten χ̃ und ϕ̃ der Wellenfunktion herleiten,
ϕ̃ = (2mc2 + i~
∂
~ χ̃ .
− eΦ)−1 c~σ (~
p − eA)
∂t
(III.71)
III.3. ÜBERGANG ZU SCHRÖDINGER-ÄHNLICHEN GLEICHUNGEN
19
Abb. III.5: (a) Die Übergänge, die zur Balmer-alpha Linie zwischen n = 3 und n = 2 in
Wasserstoff beitragen. (b) Die beobachteten relativen Intensitäten von den Linien (a), (b)-(g).
Da (b) und (g) dieselben oberen Zustand haben, ist die Verschiebung der Linien nur aufgrund
der 2p3/2 − 2p1/2 Energie-Differenz. Laut Dirac-Theorie, sollen die (d) und (e) Linien gleich
sein, wie auch die Linien (f) und (g). Die Unterschiede im Spektrum tauchen aufgrund der
Lamb-Verschiebung auf.
~ erhalten wir
Für nicht so starke Felder A
ϕ̃ '
1
c~σ · p~χ̃ .
2mc2
(III.72)
Diese Näherung führ weiter für die zwei Komponenten zu
~ ψ̃ =
α
~ ·E
!
~ ϕ̃
~σ · E
=
~ χ̃
~σ · E
~ 1 2 c(~σ · p~)χ̃
(~σ · E)
2mc
~ χ̃
~σ · E
!
,
(III.73)
was mit Hilfe der Beziehung
(~a · ~σ )(~b · ~σ ) = ~a · ~b + i~σ · (~a × ~b) ,
(III.74)
und den Kreuzprodukt-Eigenschaften dann ergibt
~ ψ̃ =
α
~ ·E
~
E
p+
2mc (~
i(~
p × ~σ ))χ̃
~ χ̃
~σ · E
!
.
(III.75)
20
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Unsere Gleichung für die große Komponente wird dann, mit der Einführung vom Bohrschen
Magneton µB = e~/(2m) = 5, 788 × 10−5 eV/T,
#
"
∂
~ 2
(i~ ∂t
− eΦ)2
∂ χ̃
iµ
(~
p − eA)
µ
B
B
~−
~ p × ~σ ) +
~ · p~) χ̃ .
i~
− µB ~σ · B
E(~
(E
=
+ eΦ −
∂t
2m
2mc2
2mc2
2mc2
(III.76)
Wegen der durchgeführten Nährungen ist die Hermizität in den beiden letzten Summanden
verletzt. Die Rekonstruktion der Hermizität lautet
µB 1 ~
~ · p~ − ~σ (~
~ + i~
~ = µB 2~σ (E
~ × p~) + i~~σ ∇ × E
~ + ~∇E
~ .
~
σ
(
E
×
p
~
)
−
i
E
p
×
E)
p
·
E
2mc2 2
4mc2
(III.77)
Jetzt kann man eine Schrödinger-ähnliche Gleichung für die große Komponente schreiben,
"
~ 2
∂ χ̃
(~
p − eA)
i~
=
+ eΦ
∂t
2m
#
∂
− eΦ)2
(i~ ∂t
µ
B
~−
~ × p~) + i~~σ ∇ × E
~ + ~∇E
~ χ̃ .(III.78)
− µB ~σ · B
−
2~σ (E
2mc2
4mc2
Das gleiche Ergebnis—eine aus der Dirac-Gleichung hergeleitete Spin-abhängige Schrödingerartige Gleichung—erhält man mit Hilfe der Foldy-Wouthuysen Transformation. Die FoldyWouthuysen-Transformation gestattet eine Darstellung der Dirac-Gleichung, bei der die oberen
zwei Komponenten des Spinors möglichst wenig mit den unteren zwei verkoppeln. Dazu versucht man, die “ungeraden” (d.h. koppelnden) Anteile im Dirac-Hamilton-Operator mittels einer
unitären Transformation zum Verschwinden zu bringen. Ein ungerader Operator ist beispielsweise α
~ , der die oberen und unteren Komponenten vermischt. Im allgemeinen ist die völlige
Entkopplung nur näherungsweise möglich und nur für die freie Dirac-Gleichung exakt durch die
Transformation
Hf := eiSf He−iSf = eiSf βe−iSf cβ~
αp~ + mc2 .
(III.79)
mit dem Operator S sei definiert durch
Sf := −
i
β~
αp~f (p) ,
2mc
(III.80)
mit f (p) eine reellwertige Funktion des Operators p. Für die Interpretation des Terms
(i~∂/∂t−eΦ)2
machen wir zuerst die Bemerkung, dass in nullter Ordnung wir die Schrödinger2mc2
Gleichung erhalten,
~ 2
∂ χ̃
(~
p − eA)
i~
− eΦ χ̃ =
χ̃ .
(III.81)
∂t
2m
Wir können also den untersuchten Term mit Hilfe des Impulses schreiben,
∂
~ 4
(i~ ∂t
− eΦ)2
(~
p − eA)
=
.
2mc2
8m3 c2
(III.82)
Die Entwicklung des relativistischen Energieausdrucks
~ 2 c2 + m2 c4
(~
p − eA)
1/2
= mc2 +
~ 2 1 (~
~ 4
(~
p − eA)
p − eA)
−
+ ...
2m
8 m3 c2
(III.83)
lässt uns erkennen, dass dieser Term eine relativistische Korrektur der kinetischen Energie
darstellt.
III.4. DIE LAMB-VERSCHIEBUNG
21
Wenn man jetzt den Ausdruck (III.78) für den Fall eines Zentral-Feldes mit V (r) = −eΦ(r)
~ = 0 anwenden, erhält man
und A
∆V
,
e
~.
~ × p~ = −∇Φ × p~ = 1 dV L
E
er dr
~ = −∆Φ =
∇E
(III.84)
Damit lässt sich der Hamiltonoperator der aus der Dirac-Gleichung hergeleiteten Schrödingerähnliche Gleichung für die große Komponente wie folgt schreiben:
H=
p2
− eΦ
|2m {z }
nicht−relativistisch
−
p4
3 2
|8m{zc }
rel. Korrektur
+
~ ·S
~
~2
~2 1 dV L
+
∆V .
2 2
2
2 c2
|2m c r{zdr ~ } |2m {z
}
Spin−Bahn−Kopplung
(III.85)
Darwin−Term
der kinetischen Energie
Damit haben wir den vollen Ausdruck eines Hamiltonoperators, welcher mit Hilfe der
Schrödinger-Gleichung die Ergebnisse von der Dirac-Gleichung für das Elektron reproduziert.
Die relativistischen Korrekturen können als Störung für den nicht-relativistischen Hamiltonoperator betrachtet werden und mit Hilfe der Störungstheorie behandelt werden. Der erste Term
nach dem nicht-relativistischen Hamiltonoperator ist die relativistische Korrektur (in v 2 /c2
Ordnung) der kinetischen Energie, manchmal auch relativistische Massenkorrektur genannt.
Der zweite Term ist durch die Spin-Bahn Wechselwirkung gegeben. Der letzte Term ist eine
relativistische Korrektur (wieder in v 2 /c2 Ordnung) zu dem Potential und trägt den Namen
C. G. Darwins, da er derjenige war, der die Rekonstruirung der verletzten Hermizität (III.77)
eingeführt hat und damit die aufgetauchten Schwierigkeiten lösen konnte. Für Systeme mit
nur einem Elektron ergibt ∆V ∼ δ(~r), so dass der Darwin-Term nur für die Energie der
Zustände mit l = 0 eine Rolle spielt. Dieser Term ist auch für die sogenannte Zitterbewegung
des Elektrons zuständig. Der von der Dirac-Gleichung abgeleitete Aufenthaltsort des Elektrons
enthält eine Schwingung in der Zeit, also eine Art Zitterbewegung mit einer Amplitude
δx = ~c/m, die laut Schrödinger [Schr1930], aus der Interferenz zwischen positiven und
negativen Energiezuständen entsteht. Die Zitterbewegung des Elektrons wurde bis jetzt nie
direkt experimentell nachgewiesen, dafür aber mit einem Kalziumion simuliert [Gerr2010].
III.4
Die Lamb-Verschiebung
Strahlungskorrekturen heben die l-Entartung der Energieniveaus nach der Dirac-Gleichung auf.
Experimentell wurde das erste Mal 1947 von W. E. Lamb und R. C. Retherford nachgewiesen,
dass die 2s1/2 und 2p1/2 Energieniveaus in Wasserstoff nicht genau übereinstimmen. Allerdings
ist diese Verschiebung sehr sehr klein, was erklärt, wieso es so lange gedauert hat, bis man sie
experimentell sehen konnte. Tatsächlich wurden nach der Entwicklung der Dirac-Gleichung und
der theoretischen Erklärung der Feinstruktur viele spektroskopische Experimente durchgeführt,
um die Dirac-Theorie nachzuprüfen. Neben vielen Experimenten, die die Dirac-Theorie bestätigt
haben, gab es schon 1937 und 1938 einige Messungen von W. V. Houston und R. C. Williams,
die angedeutet haben, dass die 2s1/2 und 2p1/2 Energieniveaus eine kleine Verschiebung hatten.
Allerdings waren die Feinstruktur-Messungen von der Dopplerlinienverbreiterung so gestört, dass
man nichts Genaues darüber sagen konnte. Erst 1947 wurde die Frage der Verschiebung von
Lamb und Retherfort endgültig geklärt, weswegen die Verschiebung den Namen Lambs trägt.
22
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Die Neuigkeit bei der Messung von Lamb und Retherford war, dass sie statt optische
Spektroskopie, Mikrowellen-Techniken angewendet haben, um einen direkten RadiofrequenzÜbergang zwischen den 2s1/2 und den 2p1/2 Zustand zu treiben. Für Frequenzen von RadioWellen ist die Dopplerverbreiterung deutlich kleiner als für optische Frequenzen, so dass
man die im Experiment von Lamb und Retherford vernachlässigen konnte. Die spontane
Übergangwarscheinlichkeit ist wegen der kleinen Energie sehr klein, der induzierte Übergang
dennoch möglich. Solche Radiofrequenz Übergänge wurden im Experiment von Lamb und
Retherford zwischen den 2s1/2 und 2p1/2 und den 2s1/2 und 2p3/2 Zuständen induziert. Der
wichtigste Punkt bei dem Experiment ist, dass der 2s1/2 Zustand langlebig, also metastabil ist.
Dies bezieht sich auf die Tatsache, dass den Zerfall vom 2s1/2 Zustand zu dem 1s1/2 Grundzustand von der Auswahlregel ∆l = ±1 verboten ist, bzw. der Übergang magnetisch Dipol ist,
und für Wasserstoff über zwei Photonen läuft. Die Lebensdauer des 2s1/2 Zustandes ist 1/7
Sekunden, die vom 2p1/2 nur 1.6 × 10−9 s. Hat man also einen Strahl von Wasserstoffatomen,
die zum Teil in angeregten Zuständen mit n = 2 sind, zerfallen schnell die Atome, die sich
in den 2p Orbitale befinden, während die in 2s1/2 in diesem Zustand bleiben. Im Experiment
von Lamb und Retherford wurde ein Strahl von Wasserstoffatomen in ihrem Grundzustand mit
einem Elektronenstrahl mit Energien von etwa 10.2 eV gekreuzt, wie in Abb. III.6. Dies führte
zu Anregungen in die n = 2 Schale, so dass etwa ein Atom in 108 zu den 2s1/2 , 2p1/2 oder 2p3/2
Zuständen angeregt wurde. Die Atome in dem langlebigen 2s1/2 Zustand können den Detektor noch in dem metastabilen Zustand erreichen, während die Atome in den 2p1/2 oder 2p3/2
Zuständen bis zum Detektor zum Grundzustand zerfallen. Ist der Detektor nur für angeregte
Atome empfindlich, kann man nur die Atome im metastabilen Zustand messen.
Abb. III.6:
Schematische Darstellung des Lamb-Retherford-Experiments. Das kollimierte
Strahlenbündel von Wasserstoffatomen kommt aus dem Ofen. Einen kleinen Anteil der Atome
wird durch Elektronenstöße in die n = 2 Schale angeregt. Der Strahl wird dann durch einen
Bereich mit Radiofrequenz elektromagnetischem Feld geführt, bevor er den Detektor erreicht.
Der Detektor registriert nur Atome in Zuständen mit n = 2.
Die Energiedifferenz zwischen den 2s1/2 und 2p1/2 Zustände kann in diesem experimentellen
Aufbau gemessen werden, indem man zwischen Produktion und Detektion einen Radiofrequenzfeld einschaltet. Wenn die Frequenz genau der 2s1/2 − 2p1/2 oder 2s1/2 − 2p3/2 Energiedifferenz
entspricht, treibt das Feld Übergänge zwischen den Zuständen, entvölkert den metastabilen
Zustand und sinkt damit die Messungsrate am Detektor. Mit dieser Methode konnten Lamb und
Retherford sowohl die Zeeman-Komponenten der 2s1/2 , 2p1/2 oder 2p3/2 Zuständen abtrennen,
als auch die von elektrischen Feldern verursachte Störung (den Stark-Effekt) reduzieren. Ihre
Messung zeigte, dass der 2s1/2 Zustand etwa 1000 MHz oberhalb des 2p1/2 Zustandes liegt.
Weitere Experimente von S. Triebwasser, E. S. Dayhoff und W. E. Lamb 1953 haben den sehr
präzisen Wert (1057.77±0.10) MHz für die 2s1/2 −2p1/2 Energiedifferenz bestimmt, welche heute
under den Namen Lamb-Verschiebung bekannt ist. Dieser Wert, was 4.37462×10−6 eV in Energie
III.4. DIE LAMB-VERSCHIEBUNG
23
bedeutet, entspricht etwa ein Zehntel der Feinstrukturaufpaltung für n = 2. Eine schematische
Darstellung der Energieniveaus für n = 2 ist in Abb. III.7 dargestellt.
Abb. III.7: Feinstruktur-Aufspaltung der Spektrallinien und Lamb-Verschiebung. Die Niveaus
sind nicht maßstabgerecht dargestellt.
Die Bemühungen auf der theoretischen Seite, die Lamb-Verschiebung zu erklären, führten
zur Entwicklung der QED. Die radiativen Korrekturen zur Dirac-Theorie entstehen dann bei
der Berücksichtigung der Wechselwirkung zwischen dem Elektron und dem quantisierten elektromagnetischen Feld. Obwohl nicht alle Abweichungen von der Diracschen Theorie auf die
Quantenelektrodynamik zurückzuführen sind, werden dennoch alle diese Abweichungen unter
dem Begriff Lamb-Verschiebung zusammengefaßt. Die Hauptbeiträge sind durch die Selbstenergie und die Vakuumpolarisation gegeben, dessen Feynman-Diagramme in Abb. III.8 dargestellt
werden. Die QED, die Struktur des Kerns (Protons) und die volle relativistische Behandlung
des Wasserstoffs als Zweikörperproblem liefern außer der Vakuumpolarisation und Selbstenergie
noch verschiedene andere Korrekturen zur Diracschen Theorie, die wir hier nach der Größe ihrer
Beiträge zum Wasserstoffspektrum auflisten wollen:
• die Selbstenergie (self-energy),
• die Vakuumpolarisation (vacuum polarization),
• Rückstoßkorrekturen (recoil corrections),
• Strahlungs-Rückstoßkorrekturen (radiative recoil corrections),
• Zwei- und Drei-Schleifen-Korrekturen zur Selbstenergie (two- and three-loop corrections),
• Kerngrößenkorrektur (finite nuclear size effect).
Die Lamb-Verschiebung wird für jeden Zustand des Wasserstoffatoms einzeln ausgewertet.
Durch die Differenz der Verschiebungen der einzelenen Niveaus ergibt sich dann der Energieunterschied, der experimentell nachgewiesen wird. Die theoretisch berechtete Lamb-Verschiebung
für das Wasserstoffatom ist laut P. J. Mohr (1057.864±0.014) MHz [Mohr1975]. Man spricht bei
allen hier erwähnten Effekten von QED Korrekturen zur Diracschen Theorie, weil die Effekte
klein sind und daher störungstheoretisch behandelt werden können.
Die genaue Berechnung der Lamb-Verschiebung unter Berücksichtigung aller Beiträgen ist
jenseits des Umfangs dieser Vorlesung. Wir geben hier nur eine qualitative Beschreibung der
Lamb-Verschiebung, basierend auf die Arbeit von T. A. Welton [Welt1948]. Diese Erklärung
24
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Abb. III.8: Feynman Diagramme der Selbsenergie (a) und Vakuumpolarisation (b).
bezieht sich auf die Wechselwirkung eines nichtrelativistischen Elektrons mit den Vakuumfluktuationen des elektromagnetischen Feldes. Wie schon im Kapitel ?? erwähnt, hat ein quantisiertes
elektromagnetisches Feld Nullpunktschwingungen, selbst wenn die mittlere Feldstärke null ist.
Durch die Kopplung des Elektrons an das elektromagnetische Vakuumfeld entstehen mittlere
quadratische Abweichungen der räumlichen Koordinate des Elektrons vom Mittelwert. Diese
führen dann zu einer effektive Ausdehnung des Elektrons, als ob es nicht mehr punktförmig
wäre, sonder ein Kugel von Radius R. Da die potentielle Energie des Elektrons im Kernfeld
von seiner Position abhängt, ist sie durch die Fluktuationen des elektromagnetischen Feldes
verändert. Die Lamb-Verschiebung ist gegeben durch die Differenz in der potentiellen Energie,
1
∆V = V (~r + δ~r) − V (~r) = δ~r · ∇V + (δ~r · ∇)2 V (~r) + . . .
2
(III.86)
Da die Vakuumfluktuationen isotropisch sind, gilt
hδ~ri = 0 ,
1
h(δ~r · ∇)2 i =
h(δ~r)2 i∇2 .
3
(III.87)
Die Lamb-Verschiebung wird damit
1
h∆Ei = h(δ~r)2 ih∆V (r)i .
6
(III.88)
Für einen punktförmigen Kern haben wir
∆V =
Ze2
δ(~r) ,
ε0
(III.89)
wobei δ(~r) die dreidimensionale Dirac δ-Funktion ist. Damit erhalten wir die Lamb-Verschiebung
h∆Ei =
Ze2 1
h(δ~r)2 ihΨ|δ(~r)|Ψi .
ε0 6
(III.90)
Aus diesem Ausdruck können wir erkennen, dass die größte Energieverschiebung bei s-Zuständen
zustande kommt, da |Ψ(0)|2 6= 0. Unter Benutzung nichtrelativistischer Wellenfunktionen für
die s-Zustände erhalten wir
Ze2 1
Z3 1
h∆Ei =
h(δ~r)2 i 3 3 ,
(III.91)
ε0 6
πn a
III.4. DIE LAMB-VERSCHIEBUNG
25
mit dem Bohr-Radius a0 = ~c/(αmc2 )=0.529 å=0.529×10−10 m. Die Energie-Verschiebung des
2s-Zustands ist also positiv. Für die Berechnung der mittleren quadratischen Variation h(δ~r)2 i
fangen wir mit der klassischen Bewegungsgleichung an
e ~
~ .
δ~r¨ = − (E
+ ~v × B)
(III.92)
m
Die Magnetfeldkomponente wird in der Regel vernachlässigt. Das elektrische Feld wird quantisiert,
X
~~ ,
~ =
E
(III.93)
E
k,λ
~k,λ
wobei ~k der Wellenvektor und λ die Polarisation der Feldmode ist. Damit können wir die
Koordinaten-Variation für das Elektron als eine Summe der von einer einzelnen Mode verursachten Variationen schreiben,
X
δ~r~k,λ .
(III.94)
δ~r =
~k,λ
Die einzelne Variationen sind ergeben durch
δ~r~k,λ =
~~
eE
k,λ
mωk2
,
(III.95)
und damit unsere mittlere quadratische Variationen
~2
e2 X hE~k,λ i
h(δ~r~k,λ ) i = 2
.
m
ωk2
2
(III.96)
~k,λ
Aus der Gesamtenergie des Feldes
Z
1
~ 2 i = 1 ~ωk
~ 2 i + µ0 hH
dV ε0 hE
~k,λ
~k,λ
2
2
| {z }
(III.97)
~2 i
ε0 hE
~
k,λ
können wir die Fluktuation des elektrischen Feldes bestimmen,
~2 i =
hE
~k,λ
~ωk
,
2ε0 L3
(III.98)
wo L3 das Quantisierungsvolumen ist. Die Summe über die Feldmoden kann in einem Integral
über die Frequenz ω umgewandelt werden, wie schon im Kapitel ?? besprochen
Z
Z
X
2L3
L3
3~
... →
d
k
.
.
.
=
ω 2 dω .
(III.99)
(2π)3
π 2 c3
~k,λ
Damit erhalten wir für die mittlere quadratische Variationen
Z
e2 ~
L3 ω 3 dω
~c 2 2α
dω
2
h(δ~r) i = 2
=
.
m 2ε0 L3 π 2 c3 ω 4
mc2
π
ω
(III.100)
Als obere und untere Integralgrenze wählen wir die Bohr-Radius a0 und die ComptonWellenlänge λc ,
~ωmin = Zαmc2 ,
~ωmax = mc2 ,
(III.101)
26
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
womit unser Integral lautet
ωZmax
dω
= ln
ω
1
Zα
.
(III.102)
ωmin
Die von den Vakuumfluktuationen verursachte mittlere quadratische Variation der Elektronkoordinate ist dann
~c 2 2α
1
1
2
2 2α
h(δ~r) i =
= λc ln
.
(III.103)
ln
mc2
π
Zα
π
Zα
Für das Beispiel des Wasserstoffatoms (Z = 1) erhalten wir eine mittlere quadratische Variation
von h(δ~r)2 i1/2 =58.4 fm und eine Lamb-Verschiebung für den 2s Zustand von 2.76 µeV. Der Vergleich mit dem experimentellen Wert von 4.3 µeV zeigt, dass diese Rechnung nur qualitativ ist.
Eine präzisere Rechnung nach Bethe und Salpeter [Beth2008] oder die von P. Mohr [Mohr1975]
sind in Übereinstimmung mit dem experimentellen Wert.
Abb. III.9: Die Lamb-Verschiebung ∆E des Grundzustandes von wasserstoffähnlichen Ionen als
Funktion der Kernladung Z (mit α die Feinstrukturkonstante). Die ausgefüllten Kreise stellen
Ergebnisse von Experimenten am ESR bei der GSI Darmstadt dar, die durchgezogene Linie gibt
die Theorie wieder.
Die Lamb-Verschiebung wurde auch für andere wasserstoffähnliche Systeme gerechnet und
gemessen. Die Größe der radiativen Korrekturen wächst schnell mit der Kernladung Z,
wie in Abb. III.9 dargestellt. Für hochgeladene Ionen wo αZ groß ist, spielen auch QED
Korrekturen zweite Ordnung (s. Abb. III.10) eine Rolle. Das Beispiel der verschiedenen
Beiträge zu der Grundzustand Lamb-Verschiebung in wasserstoffähnlichem Uran U91+ ist in
der Tabelle III.10 dargestellt. Die Summe der berechneten Beiträge ergibt 463.95 eV, in guter
Übereinstimmung mit dem experimentellen Wert für die Lamb-Verschiebung des 1s1/2 Grundzustandes 468.±13. eV.
III.5. DIE HYPERFEINSTRUKTUR
27
Abb. III.10: Links: Tabelle mit den QED Beiträgen bis zur zweiten Ordnung in α für den
Grundzustand des wasserstoffähnlichen Urans U91+ . Rechts: QED Korrekturen zweite Ordnung
in α. Es handelt sich um zweiter Ordnung Selbstenergie (SESE) und Vakuum-Polarisation
(VPVP) Korrekturen und mögliche Mischungen zwischen ihnen (SEVP) und (S(VP)S).
III.5
Die Hyperfeinstruktur
Hyperfeineffekte rühren von der Wechselwirkung des Kerns mit den Elektronen her. Solche
Effekt wurden zuerst von A. Michelson 1891 und von C. Fabry und A. Perot 1897 beobachtet.
Wie ihr Name schon zeigt, verursachen diese Effekte Aufspaltungen oder Verschiebungen die
noch kleiner sind, als die Feinstruktur. Die Hyperfeineffekte sind in zwei Kategorien aufgeteilt.
Diejenige Effekte, die zu einer Aufspaltung der Niveaus führen, sind Hyperfeinstruktur-Effekte
genannt. Die Effekte die nur eine Verschiebung der Energieniveaus im Atom verursachen sind
unter dem Namen Isotopie-Verschiebungen bekannt. Die Hyperfeinstruktur-Effekte sind durch
die elektromagnetischen Multipol-Momente des Kerns verursacht, im wesentlichen durch das
magnetische Dipolmoment und das elektrische Quadrupolmoment. Die Isotopie-Verschiebungen
treten wegen der endlichen Masse des Kernes oder endlichen Ausdehnung der Kernladung auf.
Verschiedene Aspekte der Isotopie-Verschiebung und der Hyperfeinstruktur werden in dem Anhang zum Skript “Nuclear Effects in Atomic Transitions” dargestellt und werden im Skript
selbst nicht behandelt. Dieser Abschnitt bezieht sich nur auf die Hyperfeinstruktur der Atome.
III.5.1
Hyperfeinstruktur durch magnetische Dipol-Momente
Noch bevor die Sache mit dem elektronischen Spin geklärt war, hat Pauli 1924 die Hypothese gemacht, dass der Kern auch einen Gesamtdrehimpuls besitzt, den Kernspin. Die
Hyperfeinstruktur-Effekte, so Pauli, würden dann von den magnetischen Wechselwirkungen zwi-
28
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
schen Kern und den atomaren Elektronen in Bewegung verursacht. Eine Rolle dabei würde die
Orientierung des Kernspins I~ spielen. Proportional zum Kernspin I~ hat der Kern dann auch ein
~ N , mit
magnetisches Dipol-Moment M
~
~ N = gI µN I ,
M
~
(III.104)
wo µN das nukleare Magneton µN = e~/(2mp ) ist, mp die Protonenmasse, und gI der nukleare gFaktor, auch Landé-Faktor genannt. Aufgrund des Massen-Verhältnisses zwischen Elektron und
Kern ist das nukleare Magneton 1836 Mal kleiner als das Bohr-Magneton, µN = 0.03152 µeV/T.
Betrachten wir jetzt ein wasserstoffähnliches Ion mit der Kernladung Ze so dass Zα 1
~ N . Der Hamiltonoperator für so ein System kann man als
und das nukleare Dipol-Moment M
H = H0 + HM D ,
(III.105)
schreiben, wobei wir mit H0 den Hamiltonoperator in (III.85) bezeichnen, welcher sowohl die
Coulomb-Wechselwirkung als auch die relativistischen Feinstruktur-Korrekturen beinhaltet. Das
~ N verursacht die Störung HM D . Da das nukleare Dipol-Moment viel kleiner als
Dipol-Moment M
das vom Elektron ist, werden die Hyperfeinstruktur-Korrekturen im Spektrum noch viel kleiner
als die Feinstruktur-Korrekturen. Wir teilen den Störhamiltonoperator weiter in zwei Teilen
auf,
HM D = H1 + H2 .
(III.106)
Dabei beschreibt H1 die Tatsache, dass das Dipol-Moment des Kerns ein magnetisches Feld
erzeugt, welches mit der Bahn des Elektrons wechselwirkt,
H1 =
e ~
A(~r) · p~e .
m
(III.107)
~ r) erzeugt von einem punktförmigen Dipol am Koordinatenursprung ist
Das Vektorpotential A(~
gegeben durch [Jack2006]
µ0 ~
1
µ0 ~
~
A(~r) = −
MN × ∇
=
MN × ~r .
(III.108)
4π
r
4πr3
Damit erhält man für den Hamiltonoperator H1 den Ausdruck
H1 =
µ0 2
1
~,
gI µB µN 3 I~ · L
4π ~2
r
(III.109)
wobei ~l den Bahndrehimpuls des Elektrons bezeichnet. Dieser Term ist auch Kern Spin-BahnWechselwirkung genannt, und verschwindet für elektronische Zustände, die l = 0 haben, also
für die s-Orbitalen.
Der zweite Term in (III.106) beschreibt die Wechselwirkung zwischen dem Elektronen-Spin
(mit dem entsprechenden elektronischen Dipol-Moment m
~ S ) und dem magnetischen Feld des
Kerns,
~
~.
~ = 2µB S B
H2 = −m
~S ·B
(III.110)
~
Das Magnetfeld vom Kern ist gegeben durch
µ
1
1
0
~ =∇×A
~=−
~ N∆
~ N · ∇)∇
B
M
− (M
.
(III.111)
4π
r
r
III.5. DIE HYPERFEINSTRUKTUR
29
Damit erhält man für den Hamiltonoperator H2 , auch Spin-Spin Wechselwirkung genannt, den
Ausdruck
1
µ0 2
1
~
~
~
~
H2 = −
gI µB µN (S · I)∆
− (S · ∇)(I · ∇)
.
(III.112)
4π ~2
r
r
Nach weiteren einfachen Schritten und mit der Bemerkung, dass ∆ 1r = −4πδ(~r), erhalten wir



~ r)(I·~
~ r)
2(S·~
1

~
~
S·I −
für l 6= 0
µ0 2
r3
r2
~ · Iδ(~
~ r) −

(III.113)
H2 =
gI µB µN 4π S
2
4π

4π ~
~
~
S · Iδ(~r)
für l = 0
3
Wir wollen jetzt die von dem Störhamiltonoperator (III.106) verursachte EnergieVerschiebung in erster Ordnung in der Störungstheorie berechnen. Dabei betrachten wir zuerst
den Fall mit l 6= 0. Unser Störhamiltonoperator HM D erhält in diesem Fall den Ausdruck
HM D =
µ0 2
1 ~ ~
·I,
gI µB µN 3 G
4π ~2
r
(III.114)
~ =L
~ −S
~ + 3(S
~ · ~r)~r/r2 benutzt haben. Analog zur Spin-Bahn-Kopplung,
wo wir die Notation G
ist die Diagonalisierung des Störhamiltonoperators viel vereinfacht durch die Einführung des
atomaren Gesamtdrehimpulses (also Kern und Elektron zusammen)
F~ = I~ + J~ ,
(III.115)
~ +L
~ der Gesamtdrehimpuls des Elektrons. Die Eigenwerte von
mit I~ der Kernspin und J~ = S
2
2
~
F sind F (F + 1)~ und die von Fz mF ~. Aus der Additionsregel für Drehimpulse erhalten wir
die möglichen Werte für F ,
F = |I − j|, |I − j| + 1, . . . , I + j − 1, I + j .
(III.116)
Da F und mF gute Quantenzahlen für die Störung HM D sind, konstruieren wir am besten die
ungestörten Funktionen |lsjIF mF i als liniare Kombination von den Funktionen |lsjmj ImI i
und berechnen damit die Energie-Verschiebung für l 6= 0 in der ersten Ordnung Störungstheorie,
∆E =
µ0 2
1 ~ ~
gI µB µN hlsjIF mF | 3 G
· I|lsjIF mF i .
4π ~2
r
(III.117)
Nach weiteren einfachen Operationen s. [Bran2003] erhalten wir
∆E =
mit der Konstante
C=
C
[F (F + 1) − I(I + 1) − j(j + 1)] ,
2
(III.118)
µ0
l(l + 1)
Z3
2gI µB µN
,
4π
j(j + 1) a30 n3 l(l + 1/2)(l + 1)
(III.119)
mit a0 das Bohr’sche Radius.
Für den Fall dass l = 0, verschwindet H1 und wir erhalten den Ausdruck des
Störhamiltonoperators, auch Fermi-Kontakt-Wechselwirkung genannt,
HM D =
µ0 2
8π
~ · I~ = − µ0 8π m
~ N δ(~r) .
gI µB µN δ(~r)S
~S ·M
2
4π ~
3
4π 3
(III.120)
Auch für diesen Fall führt man den atomaren Gesamtdrehimpuls F~ an, so dass
~ · I~ = 1 [(I~ + S)
~ 2 − I~2 − S
~ 2 ] = 1 [(F~ − L)
~ 2 − I~2 − S
~ 2 ] = 1 (F~ 2 − I~2 − S
~ 2) ,
S
2
2
2
da l = 0 . (III.121)
30
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Die Energie-Verschiebung hat dann den Ausdruck
∆E =
A0
[F (F + 1) − I(I + 1) − s(s + 1)] ,
2
(III.122)
µ0
8π Z 3
.
2gI µB µN
4π
3 πa30 n3
(III.123)
mit der Konstante
A0 =
Da für l = 0, j = s, können wir die zwei Fälle zusammenfassen und einen Ausdruck der EnergieVerschiebung für beliebige Werte von l geben,
A
[F (F + 1) − I(I + 1) − j(j + 1)] ,
2
(III.124)
1
Z3
µ0
4gI µB µN
,
4π
j(j + 1)(2l + 1) a30 n3
(III.125)
∆E =
mit
A=
was unabhängig von F ist. Ein anderer Ausdruck für die Energie-Verschiebung ist
∆E =
me Z 3 α2 F (F + 1) − I(I + 1) − j(j + 1) me c2 2
gI 3
α .
mp
n
j(j + 1)(2l + 1)
| 2{z }
(III.126)
13.6 eV
~ ein Feinstruktur-Energieniveau, welches den Quantenzahlen j und
Für einen Kern mit Spin I,
l entspricht, wird in weitere Hyperfeinkomponenten F gespalten. Da die Energie-Verschiebung
nicht vom mF abhängen, ist jede Hyperfeinkomponente immer noch (2F + 1) entartet. Ein
Feinstruktur-Energieniveau spaltet sich in einem Hyperfeinstruktur-Multiplett mit (2j + 1)
Niveaus, wenn I ≥ j oder mit (2I + 1) Niveaus, wenn j ≥ I. Dies erlaubt die Bestimmung
von I wenn j groß genug ist. Für “normalen” Wasserstoff (mit einem Proton als Kern), ist
der Kernspin I = 1/2 und die Hyperfeinstruktur ist für alle j-Werte ein Doublet. Für Deuterium, ein Wasserstoffatom mit einem Proton und einem Neutron im Kern und I = 1, erhalten
wir ein Doublet für j = 1/2 und Tripletten für alle andere Werte von j. Die Hyperfinestruktur für die zwei Wasserstoffisotopen ist in Abb. III.11 dargestellt. Die Intervall-Regel für die
Magnetisch-Dipol Hyperfeinstruktur ist gegeben durch
∆E(F ) − ∆E(F − 1) =
A
[F (F + 1) − (F − 1)F ] = AF ,
2
(III.127)
also proportional zu F . Man kann auch die Energie-Aufspaltung δE zwischen den zwei äußersten
Komponenten eines Hyperfeinstruktur-Multipletts (Fmax = I + j und Fmin = |I − j| bestimmen,
(
2
I + 1/2 für j ≤ I ,
4Z 3 α2 me2c α2
me
δE =
gI 3
(III.128)
I(j+1/2)
mp n (j + 1)(2l + 1)
für j ≤ I .
j
Aus dieser Aufspaltung lässt sich der nukleare g-Faktor gI bestimmen. Fürs Wasserstoffatom,
z.B., mit Z = 1, I = 1/2, gI = 5.5883, ist die Energie-Aufspaltung
δE =
me
j + 1/2
gI 2α2 3
13.5 eV ,
mp
n j(j + 1)(2l + 1)
(III.129)
was für den Grundzustand ergibt
δE(n = 1, j = 1/2, l = 0) =
8
me
gI α2 13.5 eV = 5.88 × 10−6 eV .
mp
3
(III.130)
III.5. DIE HYPERFEINSTRUKTUR
31
Diese Übergangsenergie entspricht 1420 MHz und einer Wellenlänge von 21 cm. Der von H. M.
Goldenberg, D. Kleppner und N. F. Ramsey 1960 entwickelte Wasserstoff-Maser bezieht sich
auf diesen Übergang und hat einen sehr präzisen Wert für die Übergangsfrequenz geliefert, ν =
1420405751.800±0.028 Hz. Der Vergleich mit dem theoretischen Wert ν = 1420, 45199(10) MHz
zeigt, dass die obige einfache erster Ordnung Störungstheorie mit dem experimentellen Ergebnis
innerhalb von 0.1% übereinstimmt. Mehr über weitere Korrekturen, Übergänge zwischen Hyperfeinniveaus, die Cesium-Atomuhr und Hyperfeinstruktur-Experimente befindet sich im Anhang
“Nuclear Effects in Atomic Transitions”.
Abb. III.11: Die Hyperfeinstruktur für die n = 1 und n = 2 Niveaus von Wasserstoff und
Deuterium (nicht maßstabgerecht dargestellt).
III.5.2
Hyperfeinstruktur durch das nukleare Quadrupol-Moment
Eine andere wichtige Kernstruktur-Eigenschaft ist das elektrische Quadrupolmoment, definiert
als eine Summe über alle Protonen p im Kern,
X
Qij =
3xpi xpj − δij Rp2 , (i, j = 1, 2, 3) .
(III.131)
p
~ p die Protonkoordinate im Schwerpunktsystem des Kernes. Meistens bezeichnet man
Hier ist R
die Größe des Quadrupolmoments als der Erwartungswert der z-Komponente in dem Zustand
|I, MI = Ii, also
Q = hI, MI = I|Qzz |I, MI = Ii = hI, MI = I|
X
3Zp2 − Rp2 |I, MI = Ii ,
(III.132)
p
was eine Flächedimension hat und normalerweise in barn (10−24 cm2 ) gegeben ist. Ein Kern
mit einer kugelsymmetrischen Ladungsdichte hat kein elektrisches Quadrupolmoment, da Q =
0. Das Quadrupolmoment zeigt also wie weit von der Kugelsymmetrie die Ladungsdichte des
Kerns ist. Für Kerne mit einer gestreckten Ladungsdichte in Richtung von I~ ist Q > 0 und
man bezeichnet den Kern als prolat. Ist die Ladungsdichte abgeplattet, haben wir Q < 0
und man bezeichnet den Kern als oblat, s. Abb. III.12. Der Wechselwirkungshamiltonoperator
32
KAPITEL III. WASSERSTOFF-ÄHNLICHE ATOME
Abb. III.12: Mögliche Kernladungsdichten: kugelsymmetrisch (links), prolat (mitte) oder oblat
(rechts).
zwischen dem elektrischen Quadrupolmoment des Kerns und dem von dem Elektron erzeugten
elektrostatischen Potential am Kern Ve ist gegeben durch [Rams1953, Casi1963]
3~
HEQ = B 2
~ I~ · J~ + 1) − I~2 J~2
I · J(2
,
2I(2I − 1)j(2j − 1)
(III.133)
mit der Quadrupolkonstante B
B=Q
∂ 2 Ve
∂z 2
,
(III.134)
mit
∂ 2 Ve
∂z 2
=
2 2
∂ Ve 3z − r2 j, mj = j 2 j, mj = j = − j, mj = j j, mj = j
∂z
r5 (III.135)
ist der Erwartungswert des vom Elektron erzeugten elektrischen Feldgradients am Kern. Für
eine kugelsymmetrische elektronische Ladungsverteilung (die s-Zustände mit j = 1/2) verschwindet h∂ 2 Ve /∂z 2 i und es gibt keine Quadrupolwechselwirkung. Kerne mit I = 0 oder
I = 1/2 haben kein elektrisches Quadrupolmoment. Für alle andere Systeme, kann man die
Energie-Verschiebung in erster Ordnung berechnen,
B 32 K(K + 1) − 2I(I + 1)j(j + 1)
∆E = hjIF mF |HEQ |jIF mF i =
,
4
I(2I − 1)j(2j − 1)
(III.136)
mit der Notation
K = F (F + 1) − I(I + 1) − j(j + 1) .
(III.137)
Die gesamte Energie-Verschiebung kann man jetzt als Summe von der magnetischen und elektrischen Wechselwirkung in (III.124) und (III.136) schreiben,
∆E =
B 3 K(K + 1) − 2I(I + 1)j(j + 1)
A
K+ 2
.
2
4
I(2I − 1)j(2j − 1)
(III.138)
Da die Quadrupol-Hyperfeinstruktur der Intervall-Regel nicht folgt, hat die gesamte EnergieVerschiebung eine unregelmäßige Struktur, wie in Abb. III.13 dargestellt. Das Intervall zwischen
zwei Hyperfeinstruktur-Komponenten ist gegeben durch
∆E(F ) − ∆E(F − 1) = AF +
B 3F (2F 2 + 1) − 6F [I(I + 1) + j(j + 1)]
.
4
I(2I − 1)j(2j − 1)
(III.139)
III.5. DIE HYPERFEINSTRUKTUR
33
Genau wie bei der magnetischen Hyperfeinstruktur, ist jedes Niveau (2F + 1)-fach entartet.
Diese Entartung kann durch ein äußeres Magnetfeld gehoben werden, was dem Zeeman-Effekt
für Hyperfeinstruktur-Komponenten enspricht.
Abb. III.13: Hyperfeinstrukturschema für j = 1 und I = 3/2 für das Beispiel des Quecksilberatoms 201 Hg. Das Feinstrukturniveau (links) wird von der magnetischen Wechselwirkung
(mitte) und der elektrischen Wechselwirkung (rechts) gespalten. Verlgleich mit (III.138).