Das unfassbare Elektron
Werbung

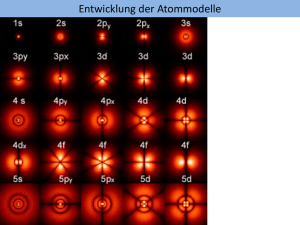
Das unfassbare Elektron Niels Bohr Nobelpreis für Physik 1922 Bohrsches Atommodell Leistungen des Bohrschen Atommodells Erklärung der Ionisierungsenergien Leistungen des Bohrschen Atommodells Erklärung der Linienspektren Gleichzeitige Bestimmung des Ortes und der Geschwindigkeit eines Autos Werner Heisenberg Nobelpreis für Physik 1933 Werner Heisenberg Die Unschärfe-Beziehung widerspricht dem Bohrschen Atommodell Neue Beschreibung des Elektrons Wellencharakter des Elektrons theoretische Vorhersage Prince Louis-Victor Pierre Raymond de Broglie Louis de Broglie Wellencharakter des Elektrons Nachdem Albert Einstein die einseitige (!) Doktorarbeit von L. de Broglie gelesen hatte, schrieb er an Max Born: „Das müssen Sie lesen! Wenn es auch verrückt aussieht, so ist es doch durchaus gediegen“ Wellencharakter des Elektrons experimenteller Nachweis Experiment Ergebnis Interferenz der Elektronenwellen Experiment Interferenz der Elektronenwellen an einem Graphitkristall Experiment Interferenz der Elektronenwellen an einem Graphitkristall Louis de Broglie Nobelpreis für Physik 1929 Clinton J. Davisson Nobelpreis für Physik 1937 Elektron als Welle mathematische Beschreibung Erwin Schrödinger Nobelpreis für Physik 1933 Elektron als Welle mathematische Beschreibung Elektron als Welle Deutung der Wellenfunktion Max Born Nobelpreis für Physik 1954 Elektron als Welle Aufenthaltswahrscheinlichkeit Zweidimensionale Wahrscheinlichkeitsfunktion © McGraw-Hill Companies Inc. Elektron als Welle Aufenthaltswahrscheinlichkeit Dreidimensionale Wahrscheinlichkeitsfunktion © Brooks/Cole - Thomson Elektron als Welle eingesperrt in einem Atom Eindimensionale stehende Wellen Elektron als Welle eingesperrt in einem Atom Zweidimensionale stehende Wellen Zweidimensionale stehende Wellen Trommelfell Elektron als Welle eingesperrt in einem Atom Eindimensional Zweidimensional Elektron als Welle eingesperrt in einem Atom Dreidimensionale stehende Wellen Elektron als Welle eingesperrt in einem Atom Orbitale s-Orbital Orbitale s-Orbital Orbitale p-Orbital Orbitale p-Orbital Orbitale d-Orbitale Elektron als Welle eingesperrt in einem Atom • Nur bestimmte Zustände sind möglich • Unschärfebeziehung ist erfüllt • Die Elektronen fallen nicht in den Kern Wellenbeschreibung des Elektrons Wellenmechanik Energie kann sich nur stufenweise ändern Quanten = Energieportionen Quantenmechanik Besetzung der Orbitale