v - WWW-Docs for TU

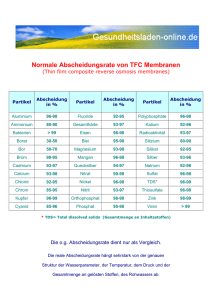
Master Umweltingenieur, 1. Semester, Modul 42439, „Strömungsmechanik“,
420607, VL, Do. 11:30-13:00, R. 3.21
420608, UE, Do. 13:45-15:15, R. 3.17
Materialien WS 2014/15
Dozent: Dr. Andreas Will
[email protected]
◦ Thermodynamisches Gleichgewicht und
Zustandsgrößen
◦ evaporation/condensation
◦ melting/freezing
◦ sublimation
◦ physical conditions for vapor, liquid and solid state
◦ Internal energy of water
◦ mechanic and kinematic properties of liquid water
◦ Solubility
A. Will
Physics of Fluids
Vorlesung 3: Zustandsgleichung:
Zustandsgrößen
• Klassische Mechanik:
• Massenpunkt: Jedes Massenelement (Partikel) mi wird vollständig durch den Ort ri und die
Geschwindigkeit i beschrieben.
• Die Bewegung wird durch die Newton‘schen Bewegungsgesetze deterministisch beschrieben
wenn die Anfangsbedingung vollständig bekannt ist.
• Kinetische Gastheorie beschreibt die mittleren (makroskopischen) Eigenschaften einer großen Zahl
(N) von Partikeln in Abhängigkeit von den (mikroskopischen ) Eigenschaften und Bewegungen der
einzelnen Partikel. Hierzu werden (makroskopische) Zustandsvariablen wie Temperatur (T), Druck
(p) and Dichte ( ) eingeführt:
• N ≈ NA≈ 6,022 141 29 *1023 (Avogadro-konstante).
• Geschwindigkeit v = 1/NA < i> ist die mittlere Geschwindigkeit der Partikel
• Dichte = N mi/V ist Masse m der Partikel im Volumen V.
• Druck p=F/A=2/3 N<Ek,i>/V ist die Kraft F die die Partikel auf die Fläche A ausüben.
• Die innere Energie E= N <Ei> ist die kinetische Energie der Partikel (Rotations- Osizillations
und Translationsbewegungen) im volumen V.
• Temperatur T = E/c ist die Zustandsvariable, die proportional ist zur inneren Energie.
-> Ein Ensemble von Gaspartikeln ist im theromdynamischen Gleichgewicht, wenn
die Temperatur, Druck und Volumen konstant sind.
Vorlesung 3: Zustandsgleichung :
Die Zustandsgröße Druck
Druck p:
p
=F/A
=(m dv/dt) /A
= Nr2mi<vi,x > /dt /A
# Kraft pro Fläche
# Kraft ist die Impulsänderung pro Zeiteinheit
# Impulsänderung pro Zeiteinheit ist zwei Mal der Impuls des
Partikels mal Zahl Nr der reflektierten Partikel.
= Nr2mi<vi ,x> <vi,x > / (LA) # die Zeit pro Reflexion t=L/<vi,x> ist gegeben durch die
Weglänge L, die das Partikel mit seiner Geschwindigkeit <vi,x>
zurücklegt. Diese Wegstrecke ist gleich der Länge des Volumen V,
wenn die Zahl der Partikel konstant ist.
= 2Nrmi<vi,x2>/V
# Volumen ist Fläche mal dazu orthogonale Längenskala
= 2Nrmi<vi2>/(3V)
# Annahme von vx= vy= vz
= Nami<vi2>/(3V)
# Die Hälfte der Partikel bewegt sich in die positive Raumrichtung.
Die Gesamtzahl im Volument V ist deshalb 2 Nr = Na
=2/3 Na<Ei>/V
Die Druckkraft der Partikel auf eine Fläche ist gegeben durch die Impulsänderung der Partikel.
Vorlesung 3: Zustandsgleichung
Zustandsgröße Temperatur
• Thermische Energie:
E = N <Ei>
= N f/2 <Ei,f>
= N f/2 k T
= cT
c = k f/2
# die innere Energie ist gegeben durch die kinetische
Energie aller Partikel.
# die kinetische Energie eines Partikels ist gegeben
durch die kinetische Energie pro Freiheitsgrad mal Zahl der
Freiheitsgrade durch 2.
# die kinetische Energie der Partikel ist proportional zur
Temperatur. Die Boltzmannkonstante k ist eine
Naturkonstante.
# die innere Energie E ist proportional zu Ihrer Temperatur.
# Die Wärmekapazität c ist eine Materialeigenschaft, da jedes
Material eine andere Zahl von Freiheitsgraden hat.
f: degrees of freedom (translational, rotational, vibrational)
Vorlesung 3: Physical properties of water (at rest):
temperature measurements
• Temperature measurements:
• density (Galileo-thermometer (left),others (center)),
• pyrometer (here colour comparison with emitting
Wolfram-wire for high temperature range, right),
• psychrometer (temperature and humidity (via T2-T1))
Fan
Dry
temp.
humid temp.
Temp. Diff.
= (t-f)
Anal.
air
Saturated air
Humid
surface
Succed air
Vorlesung 3: Zustandsgleichung
Ideale Gasgleichung
• Gay-Lussac:
• Boyle-Mariotte:
ρT = const.
p/ρ = const.
• Ideales Gasgesetz:
• NA≈ 6,022 141 29 *1023
• R = 8,314 462 J/mol/K
• k = 1,3806488 J/K
wenn p=const.
wenn T=const.
pV = RT = NA k T
Avogadrokonstante
ideale Gaskonstante
Boltzmannkonstante
Vorlesung 3: Zustandsgleichung :
Aggregatzustände:
• Dampfphase
• Flüssige Phase
• Eisphase
• kompressible flüssige
Phase
• gasartige Phase
• superkritische
Fluidphase
Trennlinien:
• Triplepunkt
• kritische Temperatur
und Druck (Punkt)
• Sättigungsdampfdruck
Phasendiagram von Wasser
Vorlesung 3: Zustandsgleichung :
Die typischen Punkte im
Phasendiagram:
Triplepunkt:
Ttp = 273.16 K = 0 °C
ptp = 611.73Pa
Siedepunkt:
Tbp = 373.15 K = 100 °C
Pbp = 101.325 kPa = 1atm
Kritischer Punkt
Tcr = 647.00 K = 273.84 °C
Pcr = 22.064 MPa
= 217.75 atm
Phasendiagram von Wasser
Vorlesung 3: Zustandsgleichung:
Sättigungsdampfdruck über Wasser
A. Will
Physics of Fluids
Vorlesung 3: Zustandsgleichung:
Sättigungsdampfdruck über Wasser
Water
A. Will
Physics of Fluids
-10
2.15
40
55.3
0
4.58
60
149.4
5
6.54
80
355.1
10
9.21
95
634
11
9.84
96
658
12
10.52
97
682
13
11.23
98
707
14
11.99
99
733
15
12.79
100
760
20
17.54
101
788
25
23.76
110
1074.6
30
31.8
120
1489
37
47.07
200
11659
Dichte des Quecksilbers Hg: 13,5 g/cm3
Vorlesung 3: Zustandsgleichung:
Dichte von Wasser und Eis
Das Diagram zeigt die Dichte
von Wasser und Eis bei
1013,25 hPa in Abhängigkeit
von der Temperatur.
Die relative Dichteänderung
im Temperaturbereich :
250K-300K : ∆ρ/ρ < 0,01.
A. Will
Physics of Fluids
Water and Ice density
Vorlesung 3: Zustansgleichung:
Physikalische Eigenschaften von Wasser
Die Werte der Konstanten hängen z.T. von Temperatur und Druck ab:
Größe
Density (maximum)
Mol mass
Melting Point
Boiling Point
Triple Point
Critical Point
Satur. vap. pressure E
Specific heat capacity
Heat conductivity
Evaporation heat
Melting heat
Viscosity
Index of refraction
Permittivity
Albedo, liquid water
ice
Solubility of NaCl
A. Will
Physics of Fluids
Symbol
= m/V
mH2O NA
Tmp
Tbp
(Ttp , ptp )
(Tcr , pcr )
c=dQ/m dT
He
Hm
n=c0/cm
α(ϑ)
α (ϑ)
s
Wert
= 0,999975 g/cm³
= 18,01528 g/mol
= 0 °C
= 100 °C
= (0 °C , 611,66 Pa)
= (373,946 °C , 22,064 Mpa)
= 23,3854 hPa
= 4.183 kJ/(kg·K)
= 0,5984 W/mK
= 2.257 MJ/kg
= 0.334 MJ/kg
= 1,001 mPa s
= 1,33251
= 80,35 A s /(V m)
0.05-0.9
0.5-0.7
360,9 g/kg
bei
(3,98 °C)
(1013,25 hPa)
(1013,25 hPa)
(322 kg/m³
(20 °C)
(20 °C, 0,1 MPa)
(20 °C, 0,1 MPa)
(100°C)
(0°C)
(20 °C, 1013,25 hPa)
(25 °C, visible) / 1,310 (ice)
(20 °C und 0 Hz)
(20 °C, 1013,25 hPa)
Ideales Gas: Volumen V=22,4 l/mol (at 1013,25hPa and 293,15 K)
Abgeleitete Größen: v(1013,25mBar, 293,15 K)
= 18,01528 g/mol / (22,4 l/mol) = 0,80 kg/m3
Vorlesung 3: Zustandsgleichung:
Wasserverfügbarkeit
3% Süßwasser
davon
30,1 % Grundwasser
1,2% Oberflächenwasser
davon
87% in Seen
2% in Flüssen
-------------------0,03*0,012*0,9=0,03%
verfügbares Wasser
A. Will
Physics of Fluids
Vorlesung 3: Zustandsgleichung:
Übung 1
Nehme an T= 277,15 K
1.
2.
3.
4.
Wie groß ist ein Wasserpartikel?
Wie groß ist der mittlere Abstand zwischen Wasserpartikeln bei Normaldruck (1013,25
hPa)?
Nehme eine Gleichverteilung der thermischen Energie auf die Freiheitsgrade.
1. Wie viele Freiheitsgrade hat eine Wassermolekül?
2. Wie groß ist die mittlere Geschwindigkeit eines Wassermoleküls?
3. Wie ändert sich die mittlere Geschwindigkeit eines Wassermoleküls bei einer
Temperaturerhöhung von 1K?
Funktionaler Zusammenhang von Druck und Temperatur bei Wasserdampfsättigung
1. Leite p(T) für den Sättigungsdampfdruck aus den Ergebnissen auf Folie 10
und/oder 11
2. Verwende den kritischen, Siede- und Triplepunkt, um die Parameter der Funktion
zu berechnen.
3. Berechne den Druck bei 10, 20, 40 und 80 Grad C und vergleiche die Werte mit den
gemessenen Werten in Tabelle auf Folie 11
A. Will
Physics of Fluids
Vorlesung 3: Zustandsgleichung
Übung 2
1. Wie funktioniert ein
1. Galilei-Thermometer
2. Psychrometer
Geben Sie eine qualitative Beschreibung.
2. Erstellen Sie eine Tabelle der physikalischen Eigenschaften der
Atmosphäre.
A. Will
Physics of Fluids