Kapitel IV Wärmelehre und Thermodynamik ctd.
Werbung

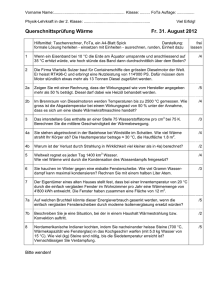
Kapitel IV Wärmelehre und Thermodynamik ctd. a) b) c) d) e) f) g) h) i) j) Definitionen Temperatur Wärme und Wärmekapazität Das ideale Gas – mikroskopisch Das idealeGas - makroskopisch Das reale Gas / Phasenübergänge Dampf, Diffusion Hauptsätze und Kreisprozesse Lösungen und Osmose Wärmeübertragung – Strahlung, Leitung, Konvektion iv) Andere Kreisprozesse Besser: Druck „in Grenzen“ halten Fläche im Indikatordiagramm größer Früher: Energieträger v. a. Kohle Heute: andere Energieträger (Sonnenenergie, Kernenergie, Gas, Kerosin, Benzin, Diesel, Biogas…..) • Stirling Prozess, Stirling Motor Wirkungsgrad TKalt η = 1− THeiß Quelle: Wikipedia 12 23 Regenerator 41 34 http://www.k-wz.de/vmotor/stirling.html • Wärmequelle – jede möglich, z. B. Sonnenenergie • Leise, viel Arbeit pro Zyklus • Sehr komplizierte Ventilsteuerung • Material für Regenerator • Ottomotor – Verbrennungsmotor (Explosion) – laut, Abgase Zur Info: 3 (V2,p3) Isochore V1 R= V2 Adiabate 2 (V2,p2) p 1 η = 1− 1 − R κ −1 4 (V1,p4) Ansaug/Auspufftakt V 1 (V1,p1) R …. Kompressionsverhältnis κ …. Adiabatenkoeff. Rmax ca. 10 • Dieselmotor -Verbrennung -laut, Abgase -Massiver als Otto-Motor Gewicht Quelle: Wikipedia Zur Info: V1 V3 R= ; R2 = V2 V2 κ 1 R 2 −1 η = 1− κ κ −1 1− R R 2 −1 R ca. 18 .. 25 R2 mögl. groß effizienter als Otto-Motor • Braytonprozess (Gasturbine, Strahltriebwerk) Quelle: Wikipedia • Sehr hohe Temperaturen (TH = 1700°C) • Kontinuierlich • Hohe Anforderung an Material • Wirkungsgrad hoch (ηtechn > 40 %) • Kältemaschine (Kühlschrank) Maschine „verkehrt herum“ laufen lassen Investiere Arbeit, pumpe Wärme von „kalt“ nach „warm“ „warm“ Umgebung, TU, „kalt“ Innenraum ∆QK „Nutzen“ (von „kalt“ nach „warm“) Leistungsziffer: L = ∆Q K = ∆W QK TK = >1 Q H − Q K TH − TK Arbeitsmedium: Fluid mit Phasenübergang bei „vernünftigen“ T und p Ausnutzung von Verdampfungswärme Quelle: Wikipedia Fluid: früher FCKW, heute FKW • Wärmepumpe pumpt Wärme von Umgebung (TK) nach Innenraum (TH) Nutzen: ∆QH Leistungsziffer QH TH ∆Q H L= = = >1 ∆W Q H − Q K TH − TK Typisch: L ungef. 5 - 6 Quelle Wikipedia analog Kältemaschine v) 2. Hauptsatz Wärme muss an „kaltes Reservoir“ abgegeben werden η < 1 Wärme Arbeit geht nicht vollständig 2 Formulierungen für 2. HS • Kelvin es gibt keinen Prozess, dessen einzige Wirkung darin besteht, dass Wärme aus einem Reservoir vollständig in Arbeit umgesetzt wird ( es gibt kein perpetuum mobile zweiter Art) • Clausius es gibt keinen Prozess, dessen einzige Wirkung darin besteht, dass Wärme von einem kalten Reservoir zu einem warmen fließt vi) Entropie und 3. Hauptsatz Carnot: TK ∆Q K η = 1− = 1− TH ∆Q H TK ∆Q K = TH ∆Q H δQ Entropie dS = T reduzierte Wärme 1) Carnot: reversibel, Ausgangszustand = Endzustand dS = 0, S ist Zustandsgröße 2) T 0 ? dS ∞, Kältemaschine: ∆W ∞ 3. Hauptsatz (Nernst) es gibt keinen endlichen Kreisprozess, durch den der absolute Nullpunkt erreicht werden könnte „der absolute Nullpunkt ist unerreichbar“ Nullpunkt von Entropie: S = 0 für T = 0K Allgemein: bei Prozess dS ≥ 0 reversibel: dS = 0 irreversibel: dS > 0 Gleiche δQ gibt unterschiedliche dS abhängig von T vii) Entropie mikroskopisch z. B.: 5 Moleküle 2 Teile „links“ „rechts“ Mikrozustand: welches Molekül ist wo (links/rechts) Makrozustand: wie viele Moleküle sind wo (links/rechts) Postulat der gleichen a-priori Wahrscheinlichkeit • 2 Moleküle, „links“, „rechts“ Makro: beide gleiche Seite; je 1 rechts/links 3 Makrozust. 2:1, 1:1, 1:2 Mikro: welche wo?: 4 Mikrozustände 3 Moleküle 1 Mikro 3 Mikro 3 Mikro 1 Mikro Makro: 3:0, 2:1, 1:2, 0:3 4 Makro Mikro: 8 N Moleküle, 2 Möglichkeiten (links / rechts) Zustand 1: alle „links“ P1 = 2-N Zustand 2: gleich viele links wie rechts N = 100 P1 = 10-30 Zust. 2 um 2N –mal wahrscheinlicher als 1 Def: S = k ln P ∆S = k N ln 2 (Unterschied zwischen Zust. 2 und 1) http://www.if.ufrgs.br/~barbosa/boltzmann.jpg Boltzmann: S = k ln W W: Zahl der Mikrozustände, die einen bestimmten Makrozustand darstellen W sehrgroße Zahl Zusammenhang mikro / makro Def. von S OH „Entropie ist Maß für Unordnung im System“ 2. HS: „Entropiesatz“ • System geht von selbst nur in einen Zustand über, der weniger geordnet ist als der Ausgangszustand • System geht von selbst nur in einen wahrscheinlicheren Zustand über viii) Freie Energie / freie Enthalpie wieso können geordnete Strukturen entstehen? System mit Umgebung Prozess spontan, wenn dSumgeb ≥ dSsystem Wärme wird an Umgebung abgegeben Erinnerung: Entropie: δQ dS = ⇒ δQ = T ⋅ dS T Dh: bei Prozess wird mindestens δQmin= T dS an Umgebung abgegeben Definiere neues TD Potential F = U – TS Freie Energie (Helmholtz) für T = const dF = dU – TdS ( - S dT) freie Energie: derjenige Anteil der Energie, der bei reversiblem isothermen Prozesses in jede beliebige Energieform umwandelbar ist. Wenn auch p = const. Definition G: G = H – TS Freie Enthalpie, Gibbs dG = dH –T dS ( - S dT) T = const freie Enthalpie: derjenige Anteil der Enthalpie, der bei reversiblem isobarem Prozesses in jede beliebige Energieform umwandelbar ist. TdS …. „Entropiesteuer an Universum“ Wichtig für chemische Reaktionen bzw.Phasengleichgewichte • Gleichgewicht dort, wo G = Min • spontane Reaktion in Richtung, in der dG < 0 i) Mischungen, Lösungen und Osmose • Alle hängen mit Entropie zusammen • Bei allen Transport von Molekülen / Materie • Mischungen: irreversible Durchmischung • Lösungen: irreversible Durchmischung • Osmose: nur scheinbar gegen Entropie i) Lösungen / Mischungen Lösung: Mischung auf molekularer Basis evtl. mit Dissoziation gelöste Ionen Stoff A im Überschuss, Stoff B sehr wenig Stoff A Lösungsmittel Stoff B gelöster Stoff Konzentration (g/L, mol/L, ....) gesättigte Lösung max. mögliche Konz. Lösung von Gas in Flüssigkeit Henry´sches Gesetz c = KH ppart c Konzentration KH Henrykonstante ppart Partialdruck Gas Ideale Lösung Raoult´sches Gesetz p Dampfdruck p A,Lös. nA xA Molenbruch = xA = p A,rein nA + nB nA, nB Molzahlen A ... Lösungsmittel, B ... gelöster Stoff Relative Feuchte definiert wie Raoult‘sches Gesetz konstante (definierte) Feuchte über gesättigten Salzlösungen (LiCl: 12%, NaCl 76%, K2SO4 97%) definierte Feuchte über Salzlösung bekannter Konzentration Lösungswärme (Lösungsenthalpie H) exotherm: Wärme wird frei, H < 0 z. B. LiCl in H2O, fast alle Gase in H2O Löslichkeit ↓ bei T ↑ endotherm: Wärme wird verbraucht, H > 0 z. B. (NH4)2SO4 in H2O Löslichkeit ↑ bei T ↑ Dampfdruck über Lösung kleiner (siehe Raoult) Siedepunktserhöhung ∆TKoch = A*b A ebullioskopische Konst. b Molalität (mol/kg) z. B. Salzwasser Gefrierpunktserniedrigung ∆TFest = B*b B kryoskopische Konst. z. B. Salzwasser (gesättigte Lösung: ∆TFest = - 18°C Elektrolytlösungen: nicht ideal Dissoziation in Ionen i (van‘t Hoff – Faktor); i ≈ Zahl der Ionen p A ,Lös. p A ,rein nA = n A + in B A Lösungsmittel B gelöster Stoff p Dampfdruck n Molzahl i van t‘Hoff-faktor Wichtige Lösungen Meerwasser ca. 35 g /kg H2O physiologische Kochsalzlösung 9.5 g /kg H2O Sodawasser, O2 in Wasser, Schlagobers, Milch, Eiweiß, Proteine, ....... ii) Osmose Diffusion: Stofftransport entlang Konzentrationsgradient keine physische Trennfläche Osmose: Stofftransport scheinbar entgegen Konzentrationsgradient Trennung durch semipermeable Membran, lässt nur kleine Moleküle durch http://www.uccs.edu/~rmelamed/MicroFall2002/Chapter%204/osmosis.jpg Transport von Lösungsmittel, bis hydrostatischer Druck ∆p = ρg∆h gleich osmotischem Druck Osmotischer Druck posm: cn=N/V, i van‘t Hoff faktor posm = cn k T posm = i cn k T k Boltzmannkonst. posm = i cm R T T Temperatur, R Gaskonst. cm=n/V molare Konz. z. B. Zuckerlösung / Wasser Wasser Zuckerlösung Lösung hohe Konz / Lösung niedr. Konz Wasser von niedrig zu hoch, bis isoton Umkehrosmose für Reinstwasser Dialyse Blutkörperchen, reines Wasser platzt Blutkörperchen, konz. Salzlösung schrumpft http://www.hgs.k12.va.us/Anatomy_and_Physiology/AandP_Powerpoints/Cells%20(3)_files/slide0134_image092.jpg j) Wärmeübertragung – Strahlung, Leitung, Konvektion • Bisher: Wärme wird aufgenommen / abgegeben Wärme – Energie, die bei Vorliegen eines Temperaturgradienten übertragen wird • Jetzt: wie wird Wärme übertragen mit / ohne Materietransport leifi.physik.uni-muenchen.de i) Wärmeübertragung durch Strahlung • Elektromagnetische Wellen • Kein Transport von Materie • Kein Medium zur Übertragung nötig • Jeder Körper sendet Wärmestrahlung aus • Spektralverteilung und Menge abhängig von Temperatur • Emission von Wärmestrahlung Abkühlung • Wärmestrahlung kann absorbiert werden Erwärmung Gleichgewicht: ein = aus, T= const. Definition: Relatives spektrales Absorptionsvermögen αλ = absorbierte / einfallende Strahlungsenergie bei λ Relatives spektrales Reflexionsvermögen ρλ = reflektierte / einfallende Str.En. bei λ Energieerhaltung: αλ + ρλ = 1 Kirchhoff‘sches Gesetz: αλ = ελ ελ rel. spektr. Emissionsvermögen ii) Schwarzer Strahler / Körper absorbiert EM Strahlung jeder Frequenz αλ = 1 für alle λ reflektiert nichts ρλ = 0 für alle λ emittiert EM Strahlung aller Frequenzen ελ = 1 für alle λ Spektralverteilung gegeben durch Planck‘sches Strahlungsgesetz 8πhf 3 I(f , T )df = c3 1 df hf exp − 1 kT Strahlungsgesetz von Planck hf << kT : 8πf 2 I(f , T )df ≈ 3 kT df c hf >> kT : 8πhf 3 hf I(f , T )df ≈ exp − df 3 c kT Rayleigh-Jeans Wien I(f,T) spektrale Strahlungsflussdichte bei T in Frequenzintervall f + df Wikipedia Aus Planck‘schem Gesetz: • Maximum der Verteilung Wien‘sches Verschiebungsgesetz λmaxT = const. = 2.9 10-3 K.m λmax Wellenl. wo max. Emission • Gesamtstrahlungsflussdichte (Integral) Stefan-Boltzmann‘sches Gesetz E = σT4 σ = 5.67 10-8 W/(m².K4) Stefan-Boltzmann-Konstante Wenn Körper nicht „schwarz“: E = α.σ.T4 oder E = ε.σ.T4 (eigentlich hier: bei allen Wellenlängen) α relatives Absorptionsvermögen, ε relatives Emissionsvermögen Real: immer Spektralbereiche, wo besser / schlechter absorbiert wird Therm. IR: fast alles „schwarz“ Sichtbares Spektrum: Farben durch selektive Absorption in einigen Spektr.Bereichen z. B.: Strahlungstemperatur der Erde ein: Solarkonstante S0 (= 1367 W/m²) davon absorbiert: 1 – Albedo (αp = 0.3) ¼ wegen Kreisfläche/Kugelfläche aus: schwarzer Körper 1 S0 (1 − α p ) = σT 4 4 1367 * 0,7 T=4 = 255K = −18°C −8 4 * 5,69 *10 z. B.: Kachelofen, Verspiegelungen, Solarduschen iii) Wärmeleitung Diffusion: Transport von Teilchen bei Konzentrationsgradient Wärmeleitung: Weitergabe von Schwingungszuständen bei Temperaturgradient Wärmetransport kein Materietransport Übertragungsmedium ist nötig Wärmeleitungsgleichung; grad T = const r J = −λ.gradT J Wärmestromdichte r r W/m² dQ = P = ∫ J.dA λ Wärmeleitfähigkeit dt W/(m.K) Stationär, Platte: P Leistung W A Q Wärme/Zeit P = λ ∆T d A Fläche d Dicke von Platte Wasser (ruhend) Gestein Feuchter Boden Org. Mat. Schnee Eis Luft Stahl Cu λ W/(m.K) 0.57 1.68 … 2.93 0.5 (Torf) … 2.2 (Sand) 0.025 (Wolle) 0.08 (Holz) 0.16 (Fett) …. 0.2 (Haut) 0.08 … 0.42 2.24 0.025 (ruhig)…125 (turb) 50 400 Gase: λ = 1/2 η.cv η Zähigkeit cv spez. Wärme (V=const.) (beide: unabh. von p) Änderung von T mit Zeit ∂T = a.∆T dt λ a= c pρ a Temperaturleitfähigkeit, Fourier-Koeff. λ Wärmeleitfähigkeit cp spez. Wärme ρ Dichte ∆ Lapl. Operator Diffusion Vergleich: Wärmeleitung r dc J = −D = − D.grad c dx r ∂c = −divJ = D div grad c = ∆c ∂t Diffusionskoeffizient D Konzentration c Strom von Molekülen J r J = −λ.gradT ∂T λ = a.∆T a = dt c pρ Wärmeleitfähigkeit λ Temperatur T Wärmestrom J Genau die gleichen Differentialgleichungen Mit Nusseltzahl (s.u.): auch für Konvektion iv) Konvektion Freie Konvektion: durch Dichteunterschied („warme“ Luft steigt auf) Erzwungene Konvektion: Strömung durch äußere Ursache (Ventilator, Pumpe, etc.) Wärmetransport und Materietransport www.hamburger-bildungsserver.de Für Konvektion: Nusseltzahl Nu = d/δ d … tats. Schichtdicke δ … Äquivalentdicke δ statt d in Wärmeleitungsgleichung einsetzen, Wärme/Zeit „normal“ ausrechnen Nu aus empirischen Formeln Kein Medium, kein Materietransport: Strahlung, prop. T4 Medium, kein Materietransport: Wärmeleitung, prop. ∆Τ Medium wird transportiert: Konvektion angetrieben durch Dichteunterschied: freie Konvektion, prop. ∆Τ angetrieben durch äußere Einwirkung: erzwungene Konvektion Ziel erreicht? • • • • Verständnis der Grundlagen Temperaturmessung Phasenübergänge und ihre Bedeutung Mikroskopische / makroskopische Betrachtung • Grundlage von Kreisprozessen • Transport von Wärme und / oder Materie