Angaben
Werbung

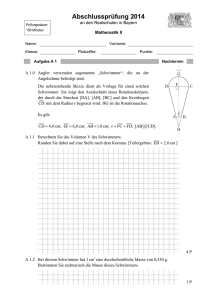
Prüfungsdauer: 150 Minuten Abschlussprüfung 2012 an den Realschulen in Bayern Mathematik I Name: Klasse: Vorname: Platzziffer: Punkte: Aufgabe A 1 Nachtermin 2 cos 6 4 und OQ A 1.0 Die Pfeile OPn () n () mit O 0 | 0 2 cos cos 3 spannen für [0;180] Dreiecke OPn Q n auf. y 1 O x 1 A 1.1 Berechnen Sie die Koordinaten der Pfeile OP1 und OQ1 für 120 und OP2 und OQ 2 für 165 . Runden Sie auf eine Stelle nach dem Komma. Zeichnen Sie sodann die Dreiecke OP1Q1 und OP2 Q 2 in das Koordinatensystem zu 1.0 ein. 2P A 1.2 Zeigen Sie rechnerisch, dass für den Flächeninhalt A der Dreiecke OPn Q n in Abhängigkeit von gilt: A() (9 cos 2 ) FE . Ermitteln Sie sodann den minimalen Flächeninhalt mit dem zugehörigen Winkelmaß . 3P Aufgabe A 2 Nachtermin I IR IR A 2.0 Gegeben sind die Funktion f mit der Gleichung y 2,5x 4 1,5 mit G I IR IR . und die Gerade g mit der Gleichung y 2 mit G y g 1 O 1 x A 2.1 Punkte A n x | 2 auf der Geraden g und Punkte Bn x | 2,5x 4 1,5 auf dem Graphen zu f haben dieselbe Abszisse x. Die Punkte A n und Bn bilden zusammen mit Punkten Cn auf der Geraden g Dreiecke A n Bn Cn . Es gilt: A n Cn 3 LE . Zeichnen Sie den Graphen zu f sowie das Dreieck A1B1C1 für x 2 und das Dreieck A 2 B2 C 2 für x 6 in das Koordinatensystem zu 2.0 ein. 2P A 2.2 Zeigen Sie, dass für die Länge der Strecken [A n Bn ] in Abhängigkeit von x gilt: A n Bn (x) 2,5x 4 3,5 LE 1P Seite - 2 - Aufgabe 2 Nachtermin A 2.3 Im Dreieck A3 B3C3 verhalten sich die Seitenlängen A3 B3 zu A3C3 wie 2 :1 . Berechnen Sie den zugehörigen Wert für x. 2P A 2.4 Im Dreieck A 4 B4 C 4 gilt: C4 B4 A 4 15 . Berechnen Sie den Flächeninhalt des Dreiecks A 4 B4 C4 . Runden Sie auf zwei Stellen nach dem Komma. 2P A 2.5 Begründen Sie, dass es unter den Dreiecken A n Bn Cn kein gleichschenkliges Dreieck gibt. 2P Seite - 3 - Aufgabe A 3 Nachtermin A 3.0 Das gleichschenklig-rechtwinklige Dreieck ABC mit der Basis [AC] ist die Grundfläche eines geraden Prismas ABCDEF. Der Punkt D liegt senkrecht über dem Punkt A. Es gilt: AB 6 cm und AD 3cm . 1 In der Zeichnung gilt: q ; 45 ; [AB] liegt auf der Schrägbildachse. 2 F D E C B A A 3.1 Punkte Pn liegen auf der Strecke [CF] . Die Winkel CAPn haben das Maß mit ]0; 19, 47] . Die Punkte Pn sind die Spitzen von Pyramiden ABCPn . Zeichnen Sie die Pyramide ABCP1 für CP1 1cm in das Schrägbild zu 3.0 ein und zeigen Sie sodann, dass für die Höhe der Pyramiden ABCPn in Abhängigkeit von gilt: CPn () 8, 49 cm tan . 2P A 3.2 Das Volumen der Pyramide ABCP2 beträgt 7 cm3 . Berechnen Sie das zugehörige Winkelmaß . Runden Sie auf zwei Stellen nach dem Komma. 2P A 3.3 Für die Höhe der Pyramide ABCP3 gilt: CP3 0,5 CF . Kreuzen Sie an, welchen Anteil das Volumen der Pyramide ABCP3 am Volumen des Prismas ABCDEF besitzt. 1 8 Seite - 4 - 1 6 1 4 1 3 1 2 3 4 1P Prüfungsdauer: 150 Minuten Abschlussprüfung 2012 an den Realschulen in Bayern Mathematik I Aufgabe B 1 Nachtermin I IR IR ) B 1.0 Punkte Cn ( x | 0,8x ) auf der Geraden g mit der Gleichung y 0,8x ( G bilden für x 0 zusammen mit den Punkten A(0 | 0) , Bn und D n Drachenvierecke ABn Cn D n mit der Symmetrieachse g. Die Winkel Bn ACn haben das Maß 60 . Punkte M n sind die Schnittpunkte der Diagonalen der Drachenvierecke ABn Cn D n . Es gilt: AM n : M n Cn 1: 3 . Runden Sie im Folgenden auf zwei Stellen nach dem Komma. B 1.1 Zeichnen Sie die Gerade g, die Drachenvierecke AB1C1D1 für x 3,5 und AB2 C2 D 2 für x 8 sowie die Diagonalen [B1D1 ] und [B2 D 2 ] mit den Diagonalenschnittpunkten M1 und M 2 in ein Koordinatensystem. Für die Zeichnung: Längeneinheit 1 cm; 2 < x < 12 ; 3 < y < 11 . 3P B 1.2 Bestätigen Sie durch Rechnung, dass für die Länge der Strecken [ABn ] gilt: 1 ABn ACn . 2 2P B 1.3 Die Punkte C n können auf die Punkte Bn abgebildet werden. Berechnen Sie die Koordinaten der Punkte Bn in Abhängigkeit von der Abszisse x der Punkte Cn . [Ergebnis: Bn (0, 60x | 0, 23x ) ] 3P B 1.4 Bestimmen Sie rechnerisch die Gleichung des Trägergraphen h der Punkte Bn . 1P B 1.5 Das Drachenviereck AB3C3 D3 hat einen Flächeninhalt von 25 FE. Berechnen Sie die Koordinaten des Punktes C3 . 3P B 1.6 Jedes Dreieck ABn Cn und das zugehörige Drachenviereck ABn Cn D n haben jeweils einen gemeinsamen Umkreis, dessen Mittelpunkt U n stets auf der Symmetrieachse g liegt. Das Drachenviereck AB4 C4 D 4 hat den Umkreismittelpunkt U 4 (5 | 4) . Zeichnen Sie das Drachenviereck AB4 C4 D 4 mit dem zugehörigen Umkreis in die Zeichnung zu 1.1 ein. Berechnen Sie sodann die Koordinaten des Punktes B4 . 3P B 1.7 Begründen Sie, dass die Winkel D n Cn Bn das Maß 60 haben. 2P Bitte wenden! Prüfungsdauer: 150 Minuten Abschlussprüfung 2012 an den Realschulen in Bayern Mathematik I Aufgabe B 2 Nachtermin B 2.0 Das gleichschenklige Trapez ABCD hat die parallelen Seiten [AD] und [BC] mit AD 12 cm und BC 6 cm . Der Mittelpunkt der Seite [AD] ist der Punkt E, der Mittelpunkt der Seite [BC] ist der Punkt F. Es gilt: EF 5 cm. Das gleichschenklige Trapez ABCD ist die Grundfläche einer Pyramide ABCDS, deren Spitze S senkrecht über dem Punkt F liegt. Es gilt: FS 10 cm. Runden Sie im Folgenden auf zwei Stellen nach dem Komma. B 2.1 Zeichnen Sie das Schrägbild der Pyramide ABCDS, wobei die Strecke [EF] auf der Schrägbildachse und der Punkt E links vom Punkt F liegen soll. 1 Für die Zeichnung gilt: q ; 45. 2 2P B 2.2 Berechnen Sie das Maß des Winkels FES und die Länge der Strecke [ES]. [Ergebnis: FES 63, 43 ; ES 11,18 cm ] 2P B 2.3 Der Mittelpunkt der Strecke [EF] ist der Punkt L. Die Parallele zu [AD] durch den Punkt L schneidet die Strecke [AB] im Punkt G und die Strecke [DC] im Punkt H. Punkte M n liegen auf der Strecke [ES] . Die Punkte M n sind die Mittelpunkte der Strecken [Pn Q n ] mit Pn [DS] und Q n [AS] . Es gilt: Pn Q n || GH . Die Winkel M n LE haben das Maß . Die Punkte G, H, Pn und Q n bilden für [0;104, 04[ gleichschenklige Trapeze GHPn Q n . Zeichnen Sie das Trapez GHP1Q1 für 85 in das Schrägbild zu 2.1 ein. Begründen Sie sodann die obere Intervallgrenze für . 3P B 2.4 Zeigen Sie durch Rechnung, dass für die Länge der Strecken [LM n ] in Abhängigkeit von gilt: 2, 24 LM n () cm. sin 63, 43 Unter den Strecken [LM n ] hat die Strecke [LM 2 ] die minimale Länge. Berechnen Sie das zugehörige Winkelmaß . 3P B 2.5 Zeigen Sie rechnerisch, dass für die Länge der Strecken [Pn Q n ] in Abhängigkeit von gilt: 2, 68 sin Pn Q n () 12 cm. sin 63, 43 4P B 2.6 Überprüfen Sie rechnerisch, ob das Trapez GHP3Q3 für 70 ein Rechteck ist. 3P Bitte wenden!