Platten4

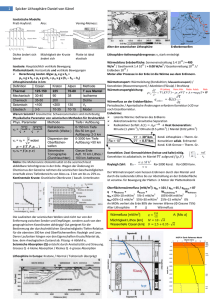
4. Von der Konvektion zur Plattentektonik
Wenn wir jetzt noch einige Lithosphärenplatten auf die Konvektionszellen packen, haben wir eine
‚Plattentektonik‘ , in der (im Gegensatz zur Kontinentalverschiebungstheorie) die Konvektion der
verantwortliche physikalische Mechanismus ist. Wieder ist das Modell noch zu einfach: Während in
den ersten Modellen die Lithosphärenplatten nur passive ‚Reiter‘ auf den Konvektionszellen waren,
haben wir jetzt Hinweise darauf, dass die Bewegung dieser Platten selbst – etwa das Eintauchen eines
subduzierten Slabs in den Mantel - eine der die Konvektion treibenden Kräfte ist. Bisher gar nicht
verstanden ist die Koexistenz von Konvektionszellen und sogenannten Plumes, unter denen man sich
‚schnelle‘ Aufströme von heißem Material vorstellt. Einige Wissenschaftler glauben, dass solche
Plumes für das Auseinanderbrechen der alten Superkontinente verantwortlich sind. So ist etwa der
jetzige Hotspot Tristan da Cunha ein Überbleibsel von einem Plume, der vor 200 Millionen Jahren
eine besonders hohe Förderleistung hatte und sich zudem genau unter Südamerika und Afrika befand
(damals als Teil von Godwanaland zusammenhängend).
4.1 Konvektionsgetriebene Plattentektonik: Drehbewegungen
‚Lithosphäre‘ bezeichnet die Kruste und den obersten Teil des Mantels der Erde, der soweit abgekühlt
und ‚versteift‘ ist, dass in ihm keine Bewegungen mehr stattfinden können – die Lithosphäre kann also
nur ‚als Ganzes‘ der Konvektionsbewegung folgen. Da diese aber an unterschiedlichen Stellen
unterschiedliche Richtungen annimmt, zerbricht die Lithosphäre zu Lithosphärenplatten, deren
Kollision zu Subduktion und deren Auseinanderdriften zu mittelozeanischen Rücken führen.
Es gibt zwei grundsätzlich unterschiedliche ‚Sorten‘ von Lithosphäre, die kontinentale und die
ozeanische. Altersbestimmung mit Hilfe der Radioaktivität: Während kontinentale Lithosphäre bis zu
3.5 Milliarden Jahre alt sein kann, hat man keine ozeanische L., die älter als 250 Millionen Jahre alt ist
, gefunden – warum? Diese Zeit ergibt sich als Verhältnis von der Größe der größten (pazifischen)
Platte zur mittleren Driftgeschwindigkeit, wie sie historisch mit seafloor spreading (s. Kap 2.2) und
heute mit dem global positioning system GPS gefunden wird. Dies ist gar nicht so unproblematisch,
denn relativ zu was soll man eigentlich die Bewegung messen? Mehr dazu in Kap. 4.3 beim hot spot
reference frame Mehr zu den Wechselwirkungen zwischen den verschiedenen Lithosphären in Kap. 5.
Die Annahme einer ‚steifen‘ oder spröden Lithosphäre, die unter zu starken Spannungen zerbricht
(anstatt sich plastisch zu verformen) ist auf einer planetaren Längenskala zulässig; wenn man dagegen
Viskosität und Schermodul innerhalb der Lithosphäre betrachtet (-> Rheologie der Erde), ist dies nicht
richtig, weil in der unteren Kruste auch plastisches Fliessen auftritt.
Eine Übersicht über die heutigen Platten:
(Jeder kennt:)
AN, Antarktika; AU, Australia; EU, Eurasia, NA North America; NB Nubia (d.h.Afrika); PA, Pacific;
SA, South America
(Wer diese Vorlesung gehört hat, sollte noch diese kennen:)
AR, Arabia; B, Borneo; CA, Caribbean; CO, Cocos; IN, India; JF, Juan de Fuca; NZ, Nazca;
SC,Scotia Sea; SM, Somalia
(Bei der 3. Gruppe sind die Grenzen nicht so klar und zT nicht durch Subduktion oder
mittelozeanischen Rücken, sondern durch starke Seismizität definiert)
CL, Caroline; I, Indo-China, NC North China; OK Okhotsk; Y, Yangtze
Wir nehmen die Vorstellung der realexistierenden Platten zum Anlass, drei verschiedenen Szenarien
von Platten-Relativbewegungen zu definieren: ridge – die Platten bewegen sich auseinander
(mittelozeanischer Rücken, z.B. mid atlantic ridge und east pacific rise), trench – die Platten bewegen
sich gegeneinander, so dass eine abtauchen muss (Tiefseegraben, z.B. Tonga-Fidji oder Mariannen),
und transforms – die Platten verschieben sich horizontal gegen einander (Transformstörung, z.B. SüdNeuseeland).
Die Kinematik der Platten beschreiben wir zunächst, unter der Annahme, dass die Erde eine Scheibe
ist, mit Euler Polen (dieses Konzept lässt sich dann gut auf eine kugelförmige Erde übertragen, s.u.).
Kinematik bedeutet Beschreibung der Bewegungen, jedoch (im Gegensatz zur Dynamik) nicht eine
Suche nach den Ursachen der Bewegung – die Einordnung dieser Kinematik in 4.1 ist also etwas
zufällig, aber wir können einige der hier eingeführten Begriffe am Ende von Kap. 4.2, wo wir
zwischen den beiden Szenarios ‚konvektionsgetriebene Plattentektonik‘ und ‚Plattengetriebene
Konvektion‘ unterscheiden wollen, ganz gut gebrauchen.
Die einfachste Plattenbewegung auf einer platten Erde ist eine kreisförmige Platte, die um ihren
Mittelpunkt rotiert. Dieser Mittelpunkt ist ihr Euler Pol, und der gesamte Rand der Platte ist eine
Transformstörung, längs derer die kreisförmige Platte sich relativ zu einer anderen, sie umgebenden
Platte bewegt. Eine etwa realistischere Plattenbewegung entsteht, wenn sich anstelle eines Vollkreises
nur ein Kreissegment verdreht, und der Euler Pol jetzt wieder der Punkt ist, um den sich die Platte
dreht, dieser Pol möge aber ausserhalb des Kreissegments liegen.
Wenn das Kreissegment wie ein Tortenstück aussieht, haben wir am äusseren und am inneren
Kreisausschnitt wieder Transformstörungen, an einer radialen Plattengrenze ein rift und an der anderen
einen trench. Wenn wir keine Kreisbewegung, sondern eine einfache lineare horizontale Verschiebung
wollen, muss der Abstand der Platte zu ihrem Euler Pol unendlich sein. Diese letzte Bedingung zeigt
schon eines der Probleme mit der Erde als Scheibe!
Beim Übergang zu einer kugelförmigen Erde entspricht dem Euler Pol im Unendlichen jetzt ein
solcher im Pol im Abstand von 90° (auf einem Großkreis), und der linearen Verschiebung entspricht
eine Verschiebung längs eines Großkreises. Vom Euler Pol aus gesehen ist diese Verschiebung aber
eine Drehbewegung! Jede Plattenbewegung auf der Kugeloberfläche kann und muss als
Drehbewegung verstanden werden. Den Euler Pol findet man, wie bei der ebenen Erde, indem man an
mindestens zwei Stellen einer Transformstörung je eine zur TS senkrechte Linie (eine Art
Radiusvektor in Bezug auf den Euler Pol) konstruiert, der EP ist der Schnittpunkt diese Linien.
Beim Vergleich des Tortenstück-Modells (mit gebogenen Transformstörungen und zu denen senkrecht
senkrechten rifts) mit realen Daten (sehr gut: der mittelatlantische Rücken im Südatlantik!) müssen
wir das Bild von den kreisförmigen Transformstörungen noch dahingehend abgeändert, dass die
Transformstörungen von kurzen, aber wieder auf ihnen senkrechten, rifts unterbrochen werden. Der im
Grossen Nord-Süd verlaufende mittelatlantische Rücken setzt sich also aus vielen kleinen TS und rifts
zusammen, weil Plattentektonik auf einer Kugeloberfläche nur Drehbewegungen zulässt. – Beim
Finden des Euler Pols muss noch zwischen scheinbarem und wahren Trend der Transformstörungen
unterschieden werden, letzteren findet man durch der Verschieben der TS längs der rifts, so dass sich
wieder ein durchgehendes Kreisstück ergibt.
Zwei weitere Methoden, den Euler Pol zu finden: 1) slip vectors, mit denen die Ausbreitungsrichtung
von an Transformstörungen entstandenen S Wellen (und damit die Richtung der transform) gefunden
wird. 2) Mit Hilfe des seafloor spreading (Kap. 2.2) wird die lineare Plattengeschwindigkeit (z.B. in
mm/jahr) als Funktion des Abstandes vom (angenommenen) Euler Pol gemessen (Zeichnung); für ein
ridge entlang eines Großkreises mit zwei Euler Polen im Abstand von 180° ergibt dies eine Sinuskurve
mit v  0 an den EP und v  vmax in der Mitte, nur für einen falsch angenommen Euler Pol verschiebt
sich dieses Maximum. Jetzt wird auch klar, warum Plattenbewegungen nicht wirklich in mm/Jahr,
sondern in °/my (Grad pro Millionen Jahren) angegeben werden.
4.2 Plattengetriebene Konvektion: endo- und exotherme Phasengrenzen
Im Modell der konvektionsgetriebenen Plattentektonik hat die Plattenbewegung keine Rückwirkung
auf das Geschwindigkeitsfeld, d.h. auf die Bewegung des Mantelmaterials. Zumindest 3 Mechanismen
für eine solche Rückwirkung sind aber vorstellbar:
1) slab pull: der bei der Subduktion in den Mantel abtauchende Teil ozeanischer Lithosphäre ist
kühler und deshalb dichter als der umgebende Mantel, er ‚fällt‘ in diesen; der Vorgang stellt
Bewegungsenergie zur Unterstützung der Konvektion bereit. Quantitative Abschätzung:
Ein Slab (=subduzierende Platte) der Mächtigkeit d und Breite W möge bis zur Tiefe D in den
Mantel mit einem Temperaturunterschied T zwischen z=0 und z=D eintauchen. Seine
Dichteanomalie (bei einem mittleren Temperaturunterschied T / 2 zum umgebenen Mantel) und
sein Volumen sind T und dWD; die (nach unten gerichtete) Auftriebskraft ist also
FB  ( T / 2)dWDg .
Diese ‚negative‘ Auftrieb wird durch viskose Reibung kompensiert, die zugehörige Kraft kann, wie
im Laborversuch, als proportional zur Viskosität  , Fläche DW und Plattengeschwindigkeit v so
wie umgekehrt proportional zur ‚Mächtigkeit der Flüssigkeits-Schicht‘ angenommen werden. Als
Mächtigkeit wählen wir die halbe Länge L/2 der Platte – in der Annahme, dass L auch die
(horizontale) Grösse einer Konvektionszelle ist und dass die Flüssigkeit zwischen der
Subduktionszone und einem hypothetischen Fixpunkt in der Mitte der Konvektionszelle geschert
vDW
wird: FV 
L/2
Aus der Gleichsetzung FB  FV ergibt sich die Geschwindigkeit des abtauchenden slabs
v
TdLg
4
Wir übernehmen
1
m2
,
  10 6
,
K
s
aus Kap. 3, aber T  1400K (Temperaturunterschied nicht für den ganzen Mantel, sondern nur
  4000kg / m3 , g  10m / s 2 ,   3 *10 5
22
kg
, und setzen
m*s
noch L  3 *10 6 m , und wählen als Mächtigkeit des slabs d=30000m, und erhalten
v  3 *10 9 m / s  0.1m / Jahr .
zwischen ‚unten‘ und ‚oben‘ bezüglich des abtauchenden slabs) und   10
Alternativ kann die Mächtigkeit d des abtauschenden slabs mit d  L / v aus den Gleichungen
entfernt werden; hierbei wird unterstellt, dass diese Mächtigkeit durch geothermische Diffusion mit
dem Abkühlalter L/v kontrolliert wird – s. Kap. 5. Dann ergibt sich die Geschwindigkeit zu
vL3 (
Tg 2
) 
4
2) ridge push: Die ozeanische Platte verjüngt sich – nicht nur in bezug auf ihr Alter, sondern
auch in bezug auf ihre Mächtigkeit, zum Mittelozeanischen Rücken hin. Dort entsteht also eine Art
schräger Rampe, auf der die Platte herunterrutscht – auch dieser Vorgang stellt Bewegungsenergie
zur Unterstützung der Konvektion bereit.
3) Durchgang der subduzierenden Platten durch Phasengrenzen im oberen Mantel. Phasengrenzen
(PG) wurden wegen des sprunghaften Anstiegs der seismischen Geschwindigkeiten zuerst mit
seismologischen Methoden gefunden. An der PG in 410 km Tiefe ändert sich die Kristallstruktur
des Olivins (Mg , Fe) 2 SiO4 , aus dem der obere Mantel grösstenteils besteht, vom Olivingitter zum
sog. Spinellgitter (dichtere Kugelpackung. Das Material ist weiterhin Olivin, der Name des
Kristallgitters ist von dem Halbedelstein Spinell entlehnt, der das gleiche Gitter hat. Diese
Phasengrenze ist physikalisch, nicht chemisch, weil die Komposition des Materials sich nicht
ändert). An der PG in 660 km Tiefe ändert sich auch die chemische Komposition, und unterhalb
haben wir anstelle des Olivins Perovskit (Mg , Fe) SiO3 und Magnesiowüstit (Mg , Fe)O .
Die Phasengrenze in 410 km Tiefe ist exotherm – dies bedeutet, dass sie im p-T Diagramm durch eine
monoton steigende Funktion dargestellt wird (positiver Clayperon slope): Zu einer niedrigeren
Temperatur gehört, an der PG, ein niedrigerer Druck. Ein abtauchende, kalte Platte (jawohl, sie ist
auch nach 100 Millionen Jahren noch kälter als der sie umgebende Mantel – wer es nicht glaubt,
berechne bitte die Abkühlzeit bei der geothermischen Diffusion, in Abhängigkeit von der Größe des zu
kühlenden Körpers) verringert also den Druck an der PG, so dass sich die dichtere, unter der PG
befindliche Hochdruckphase scheinbar der Platte ‚entgegenwölbt‘ und eine positive Dichteanomalie
erzeugt, die zu einem zusätzlichen gravitativen Zug nach untern führt – dies ist vermutlich ein
effektiverer slab pull als der unter 1) genannte Mechanismus.
Dagegen ist die Phasengrenze in 660 km Tiefe endotherm und der Clayperon slope ist negativ: Alle
o.g. Argumente drehen sich jetzt um und diese PG ‚behindert‘ das Eintauchen der Platte in den unteren
Mantel.
Nb. Jetzt kann man sich natürlich fragen, ob die subduzierenden Platten es überhaupt bis in den
unteren Mantel ‚schaffen‘. Viele Studien in seismischer Tomographie in den 90er Jahren fanden
Übereste von ozeanischen Platten, die entweder horizontal an der 660 km PG ‚entlangschrammen‘
oder aber in den unteren Mantel vordringen. Die o.g. Frage ist wegen des geringen räumlichen
Auflösungsvermögens von seismischer Tomographie in diesen Tiefen nur schwer zu beantworten – als
wahrscheinlichste Antwort gilt heute ‚es gibt beide Szenarien‘.
Bis jetzt haben wir 3 mögliche Rückwirkungen der Plattentektonik auf das Geschwindigkeitsfeld im
Erdmantel kennengelernt, so dass das 2. Szenario zumindest möglich erscheint. Können wir das
‚Funktionieren‘ beider Szenarios in Bezug auf ihre Vorhersagen zum Auftreten von ridges, transforms
und trenches, wie in 4.1 eingeführt, gegen einander abwägen? Ja, nämlich anhand von
1) Ridge offsets, also der Beobachtung, dass wir anstelle langer ridges Transformstörungen haben, die
von kurzen, aber wieder auf ihnen senkrechten, rifts unterbrochen werden. Im Bild der
konvektionsgetriebenen Plattentektonik sollten wir stattdessen lange ridges sehen, die genau über
den Aufströmen zwischen den Konvektionszellen liegen. Das 2. Szenario erklärt das Auftreten der
ridge offsets besser, weil ein grossräumiger mittelozeanischer Rücken wie der atlantische (der in
Wirklichkeit aus kurzen ridges und transforms besteht), nicht notwendig der Grenze zwischen
zwei Konvektionszellen folgen muss – nur die transforms geben die tatsächliche Richtung des
Mantelflusses an.
2) Jumping ridges, also die Beobachtung, dass ridges in Zeitabständen von wenigen Millionen Jahren
ihre Lage und Richtung ändern können. Der jüngere ridge ist dabei senkrechter zur Richtung des
spreadings als der ältere. Im 1. Szenario brauchen wir zur Erklärung schnelle Änderungen der
Lage von kleinräumigen Konvektionszellen, im 2 .Szenario dagegen nur langsame Änderungen der
Konvektionsbewegung, auf die die ozeanische Lithosphäre mit der Ausbildung neuer Risse
(cracks) reagiert. (Nach Cox & Heart – ist das wirklich überzeugend? Weiss doch keiner, wie
chaotisch und auch kleinräumig die Konvektion wirklich ist....)
3) Ridge meets trench – was passiert eigentlich, wenn ein mittelozeanischer Rücken subduziert wird?
Wenn, wie im 1. Szenario, ridges bzw. trenches genau über Auf- bzw. Abströmen von Mantel
liegen, dann müsste jetzt die Konvektion selbst behindert werden, weil Auf- und Abstrom
zusammenkommen und sich auslöschen. Im 2. Szenario wird nur die Platte zwischen ridge und
trench verschluckt.
4.3 Die Plume-Hypothese
Die meisten Vulkane auf der Erde sind durch Subduktion entstanden und befinden sich in
unmittelbarer Nähe (max. 200 km) von Subduktionszonen – verkürzt dargestellt transportiert die
Subduktion u.a. junge ozeanische Sedimente in den Mantel, und das darin enthaltene Wasser verringert
die Schmelztemperatur und macht Schmelzen wahrscheinlicher als anderswo – Genaueres siehe Kap.
5. Es gibt aber auch 50 – 100 (diese Zahl wird später diskutiert) Intraplattenvulkane, deren Entstehung
nicht mit den in 4.1 und 4.2 diskutierten Konvektionsmechanismen verknüpft zu sein scheint – ein
Musterbeispiel ist Hawaii. Die Lage dieser Vulkane korreliert keineswegs mit den Plattengrenzen, aber
‚etwas‘ mit langwelligen Geodanomalien, die durch räumliche Temperaturvariationen im unteren
Mantel entstehen. Die attraktivste Hypothese zur Entstehung dieser Intraplattenvulkane ist die von
Wilson, dass sie Oberflächensignaturen von an der Kern-Mantelgrenze aufsteigenden Aufströmen
verringerter Viskosität, sogenannter ‚Plumes‘ sind. Zur Unterscheidung von den ‚echten‘ Vulkanen
wurden sie auch hotspots genannt. In den guten alten Zeiten (also bis etwa 1998) glaubten die meisten
Geowissenschaftler, dass die Plumes fest an der Kern-Mantelgrenze ‚kleben‘ und die durch
Konvektion verursachten Horizontalbewegungen nicht oder nur mit sehr viel geringerer
Geschwindigkeit mitmachen; während die vertikale Geschwindigkeitskomponente des PlumeMaterials wegen der verringerten Viskosität um eine Größenordnung höher ist als die der
Plattenbewegungen – etwa 1m/a. Da wir an der Erdoberfläche nicht die Kernmantelgrenze, sondern
die sich bewegenden Platten sehen, bot die Vorstellung von den stationären Plumes die Möglichkeit,
einen festen Bezugsrahmen, den hot spot refence frame zu definieren, relativ zu dem sich das
Mantelmaterial und die Platten bewegen.
Die zunächst recht spekulative Hypothese hatte schnell Unterstützung der Geochemiker, die die
chemische Komposition und vor allem Isotopenverhältnisse von Erdmaterialien untersuchen: Die
chemische Zusammensetzung von Laven aus den hotspots und von Laven aus mittelozeanischen
Rücken (MORB – mid ocean ridge basalt) erwies sich als unterschiedlich – ein Hinweis darauf, dass
diese verschiedenen Vulkane aus verschiedenen Reservoiren gespeist werden, wenn auch kein
Nachweis, dass die Plumes von der Kern-Mantelgrenze kommen. Schließlich gibt es aber
geochemische Hinweise darauf, dass das Material in den Plumes Überreste ozeanischer Kruste enthält,
dies wäre dann eine Unterstützung der Hypothese von den bis in den untersten Mantel abgetauchten
subduzierten Platten.
Insgesamt kann als eine der stärksten Aussagen der Geophysik gelten, dass – infolge der Konvektion –
das Material im Mantel vermischt wird; und als die wohl stärkste Aussage der Geochemie, dass
bestimmte Reservoire gerade nicht vermischt werden.
Die Vorstellung von den ortsfesten Hotspots war nie ganz unangezweifelt: Wenn sie streng richtig
wäre, müssten die anderen hotspots mit Vulkanen in der pazifischen Platte – z.B. Marquesa, Pitcairn
und die Osterinseln – infolge der Plattenbewegung sea mount chains von der gleichen Form wie die
Hawaii-Emporer chain produziert haben. Steinberger und O’Connell (1998) zeigten mit
geodynamischen Modellrechnungen, dass die Konvektion die Plume-Aufströme verbiegen und
‚zerreißen‘ kann.
Schließlich sollen zusammen mit den Plumes noch die flood basalts erwähnt werden. Diese wirken
zunächst wie (geologisch alte) Oberflächensignaturen von Plumes, nur mit einer um 10 4...108 höheren
Förderrate an basaltischem Magma. Ein typisches Beispiel sin die indischen Deccan flood basalts, die
heute als eine (auf einer geologischen Zeitskala) kurzfristige Erhöhung der Fördermenge des heute
unter Reunion befindlichen hotspots vor 65 Millionen Jahren interpretiert werden. Da dieses Alter
genau mit der Kreide-Trias Grenze zusammenfällt, wird der ‚Super-Vulkanausbruch‘ von einigen
Autoren für das Massensterben am Ende der Kreidezeit verantwortlich gemacht. Genauso bekannt ist
die Theorie, die einen gleichalten Asteroidenimpakt bei Chixilub (Yukatan) dafür verantwortlich
macht (Alvarez et al. 1980, 1984). Für den Einfluss der flood basalts auf die Evolution spricht, dass
etwa zeitgleich mit den meisten Massensterben (mass extinction events) der letzten 250 Millionen
Jahre flood basalts aufgetreten sind (Courtillot, 1994, 2002) - allerdings sind für die viele dieser
Massensterben auch Impaktkrater mit dem richtigen Alter gefunden worden.