(Betragsungleichung.Skizzen)

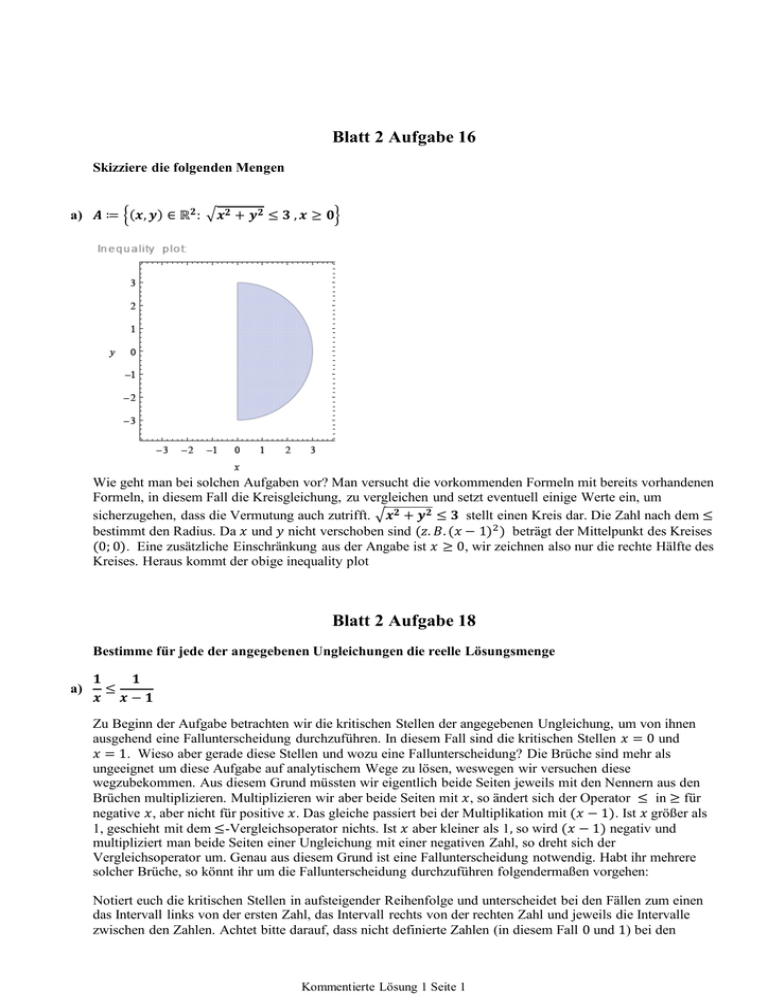
Blatt 2 Aufgabe 16
Skizziere die folgenden Mengen
a)
Wie geht man bei solchen Aufgaben vor? Man versucht die vorkommenden Formeln mit bereits vorhandenen
Formeln, in diesem Fall die Kreisgleichung, zu vergleichen und setzt eventuell einige Werte ein, um
sicherzugehen, dass die Vermutung auch zutrifft.
stellt einen Kreis dar. Die Zahl nach dem
bestimmt den Radius. Da und nicht verschoben sind
beträgt der Mittelpunkt des Kreises
. Eine zusätzliche Einschränkung aus der Angabe ist
, wir zeichnen also nur die rechte Hälfte des
Kreises. Heraus kommt der obige inequality plot
Blatt 2 Aufgabe 18
Bestimme für jede der angegebenen Ungleichungen die reelle Lösungsmenge
a)
Zu Beginn der Aufgabe betrachten wir die kritischen Stellen der angegebenen Ungleichung, um von ihnen
ausgehend eine Fallunterscheidung durchzuführen. In diesem Fall sind die kritischen Stellen
und
. Wieso aber gerade diese Stellen und wozu eine Fallunterscheidung? Die Brüche sind mehr als
ungeeignet um diese Aufgabe auf analytischem Wege zu lösen, weswegen wir versuchen diese
wegzubekommen. Aus diesem Grund müssten wir eigentlich beide Seiten jeweils mit den Nennern aus den
Brüchen multiplizieren. Multiplizieren wir aber beide Seiten mit , so ändert sich der Operator
in für
negative , aber nicht für positive . Das gleiche passiert bei der Multiplikation mit
. Ist größer als
1, geschieht mit dem -Vergleichsoperator nichts. Ist aber kleiner als 1 so wird
negativ und
multipliziert man beide Seiten einer Ungleichung mit einer negativen Zahl, so dreht sich der
Vergleichsoperator um. Genau aus diesem Grund ist eine Fallunterscheidung notwendig. Habt ihr mehrere
solcher Brüche, so könnt ihr um die Fallunterscheidung durchzuführen folgendermaßen vorgehen:
Notiert euch die kritischen Stellen in aufsteigender Reihenfolge und unterscheidet bei den Fällen zum einen
das Intervall links von der ersten Zahl, das Intervall rechts von der rechten Zahl und jeweils die Intervalle
zwischen den Zahlen. Achtet bitte darauf, dass nicht definierte Zahlen (in diesem Fall und ) bei den
Intervallen an sich nicht mit eingeschlossen sind. Auf diese Weise bekommt ihr relativ einfach die
Kommentierte Lösung 1 Seite 1
Intervallen an sich nicht mit eingeschlossen sind. Auf diese Weise bekommt ihr relativ einfach die
nachfolgenden Fallunterscheidungen.
Sei
In diesem Fall war
. Multipliziert man zunächst beide Seiten mit
, so verändert es nichts an eurem
Vergleichs-Operator, da
für
positiv ist. Das selbe gilt bei der Multiplikation von auf beiden
Seiten. Als nächstes folgt die Umformung und das Ergebnis
, da
zwar prinzipiell
immer erfüllt ist, wir aber momentan nur
betrachten.
Sei
In diesem Fall war
. Multipliziert man zunächst beide Seiten mit , so dreht sich der
Vergleichsoperator um, da negativ war. Das selbe geschieht bei
, da
für negative ebenfalls
immer negativ wird. Jetzt wird noch umgeformt und wir erhalten
, das prinzipiell immer erfüllt ist. Da
wir aber
angenommen hatten, müssen wir auch hier wieder unser Ergebnis einschränken. Heraus
kommt:
Sei
Hier befindet sich unser zwischen 0 und 1. Wer sich an dieser Stelle fragt, weshalb, sollte sich die
Kommentare nochmals komplett durchlesen (Ich erinner an die Selbstständigkeit und Durchhaltevermögen
im Studium). Wir führen zunächst eine Multiplikation auf beiden Seiten mit durch, wodurch der
Vergleichsoperator unverändert bleibt ( ist positiv, da zwischen 0 und 1). Als nächsten Schritt führen wir
die Multiplikation mit
aus und drehen den Operator um, da in diesem Fall immer kleiner als ist
und
daher negativ wird. Umformen ergibt
, was nie erfüllt ist.
Zum Schluss führen wir unsere drei Teilergebnisse zusammen und erhalten
Erstellt von: Christian Forst
Kommentierte Lösung 1 Seite 2