Lösung 7

MAE4 – Mathematik: Analysis für Ingenieure 4
Dr. Christoph Kirsch
Frühlingssemester 2016
ZHAW Winterthur
Lösung 7
Aufgabe 1 :
a) Aus der Tabelle im Kap. 1.3.5 der Vorlesung lesen wir die Wahrscheinlichkeitsdichtefunktion der exponentialverteilten Zufallsvariablen X ab:
−3x
3e , x ≥ 0
fX (x) =
.
(1)
0,
x<0
Durch Integration (Gleichung (9) der Vorlesung) erhalten wir die kumulative
Verteilungsfunktion
b
Zb
Zb
b
1 −3x −3x
(2)
e = −e−3x 0
FX (b) =
fX (x) dx = 3e
dx = 3 −
3
0
−∞
0
−3b
= −e
− (−1) = 1 − e−3b ,
b ≥ 0,
(3)
und natürlich FX (b) = 0, b < 0. Gemäss Kap. 1.5.1 der Vorlesung (Gleichung
(11)) ist die kumulative Verteilungsfunktion der transformierten Zufallsvariablen
Y gegeben durch
(
y+2
0,
y < −2
<
0
0,
y+2
4
FY (y) = FX
.
=
=
3
3
y+2
−
y+
−3 y+2
(
)
1−e 4 , 4 ≥0
4
1 − e 4 2 , y ≥ −2
(4)
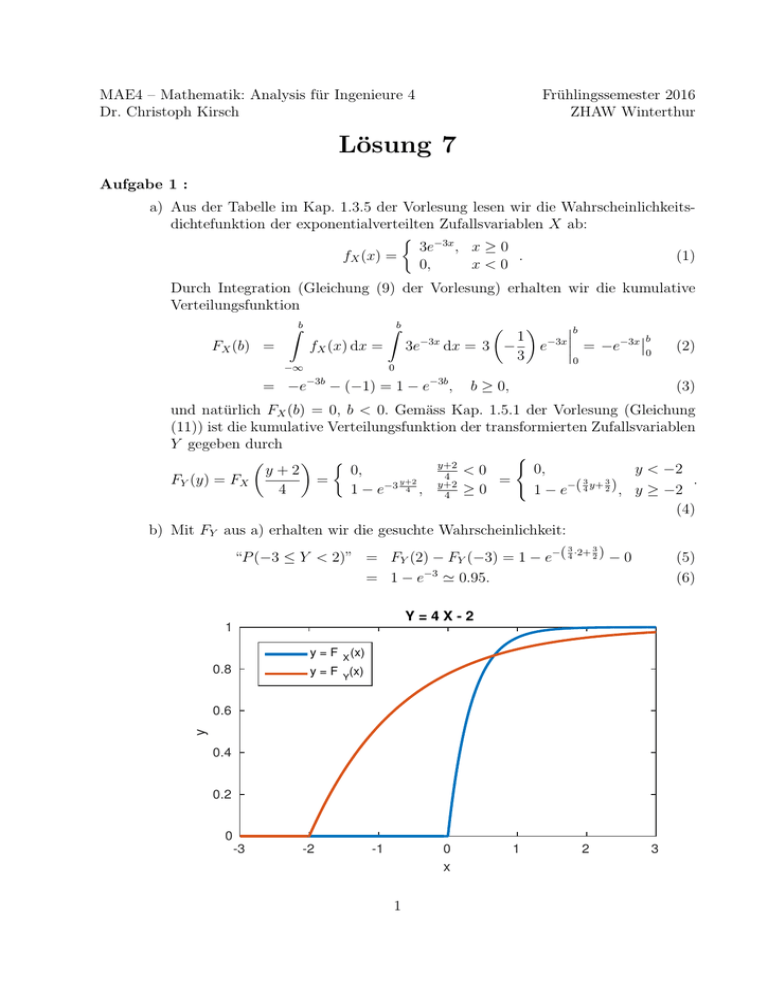
b) Mit FY aus a) erhalten wir die gesuchte Wahrscheinlichkeit:
3
3
“P (−3 ≤ Y < 2)” = FY (2) − FY (−3) = 1 − e−( 4 ·2+ 2 ) − 0
= 1 − e−3 ' 0.95.
(5)
(6)
Y=4X-2
1
y = F X (x)
0.8
y = F Y(x)
y
0.6
0.4
0.2
0
-3
-2
-1
0
x
1
1
2
3
c) Aus der Tabelle im Kap. 1.3.2 der Vorlesung lesen wir die Wahrscheinlichkeitsfunktion der binomialverteilten Zufallsvariablen X ab:
k 3−k
4
3
1
, k ∈ {0, 1, 2, 3}.
(7)
fX (k) =
5
5
k
Für die transformierte Zufallsvariable Y := 2X + 3 erhalten wir im(Y ) =
{3, 5, 7, 9} und gemäss der Formel im Kap. 1.5.1 der Vorlesung die Wahrscheinlichkeitsfunktion
fY (yi ) = fX
yi − 3
2
=
yi2−3 3− yi2−3
4
1
,
yi −3
5
5
2
3
(8)
für yi ∈ im(Y ) = {3, 5, 7, 9}.
d) Mit fY erhalten die gesuchte Wahrscheinlichkeit
“P (Y ≥ 6)” = PY ({7, 9}) = PY ({7}) + PY ({9}) = fY (7) + fY (9) (9)
2 3−2 3 3−3
3
1
4
3
1
4
=
+
' 0.10. (10)
2
3
5
5
5
5
Y=2X+3
0.6
0.5
y=f
X
y=f
(x)
Y
(x)
y
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
6
7
8
9
x
Aufgabe 2 :
Wir verwenden die Formeln aus dem Kap. 1.5.2 der Vorlesung: Falls X ∼ N (µ, σ 2 ),
µ ∈ R, σ > 0, dann ist die Verteilung der linear transformierten Zufallsvariablen Y :=
X−µ
gegeben durch Y ∼ N (0, 1) mit kumulativer Verteilungsfunktion Φ (tabelliert):
σ
x−µ
FX (x) = Φ
, x ∈ R.
(11)
σ
Wir verwenden in dieser Lösung die Tabelle aus der Formelsammlung von Papula,
S. 508.
2
a) X ∼ N (2, 5), Y :=
X−2
√
5
∼ N (0, 1).
0−2
“P (0 < X ≤ 2)” = FX (2) − FX (0) = Φ
−Φ √
(12)
5
2
2
= Φ(0) − 1 − Φ √
(13)
= Φ(0) − Φ − √
5
5
' Φ(0) − 1 + Φ(0.89) ' 0.5 − 1 + 0.8133 ' 0.31, (14)
2−2
√
5
wobei wir noch Φ(−x) = 1 − Φ(x), x > 0, verwendet haben.
X+1
3
b) X ∼ N (−1, 9), Y :=
∼ N (0, 1).
“P (X > −3)” = PX ((−3, ∞)) = 1 − PX ((−∞, −3]) = 1 − FX (−3)
(15)
−3 + 1
2
2
= 1−Φ
=1−Φ −
=1− 1−Φ
(16)
3
3
3
2
= Φ
' Φ(0.67) ' 0.7486 ' 0.75.
(17)
3
c) X ∼ N (0, 2), Y :=
X
√
2
∼ N (0, 1).
“P (X < 4)” = FX (4) = Φ
4
√
2
' Φ(2.83) ' 0.9977 ' 1.0.
(18)
Dieselben (gerundeten) Wahrscheinlichkeiten hatten wir auch schon in Serie 6, Aufgabe 4, mit MATLAB erhalten.
Aufgabe 3 :
Gemäss der Tabelle in Kap. 1.3.5 der Vorlesung ist die Wahrscheinlichkeitsdichtefunktion der Zufallsvariablen X gegeben durch
fX (x) =
3
1
,
π 9 + (x + 2)2
x ∈ R,
(19)
wobei wir t = −2 und s = 3 eingesetzt haben. Aus Kap. 1.5.1 der Vorlesung wissen
wir, dass die Wahrscheinlichkeitsdichtefunktion der Zufallsvariablen Y gegeben ist
durch
1
y−a
fY (y) = fX
= 3fX (3 (y − 5)) , y ∈ R,
(20)
b
b
wobei wir a = 5 und b =
1
3
eingesetzt haben. Damit gilt
1
3
1
9
1
9
2 =
2 =
π 9 + (3(y − 5) + 2)
π 9 + (3y − 13)
π9+9 y−
1
1
=
, y ∈ R.
π 1 + y − 13 2
fY (y) = 3
3
Es gilt also Y ∼ Cauchy
13
,1
3
.
3
13 2
3
(21)
(22)
Wahrscheinlichkeitsdichtefunktionen von X und von Y = 1/3 X + 5, wobei X ∼ Cauchy(−2,3)
0.35
Cauchy(−2,3)
Cauchy(13/3,1)
0.3
fX(x), fY(y)
0.25
0.2
0.15
0.1
0.05
0
−5
−4
−3
−2
−1
0
x, y
1
2
3
4
5
Aufgabe 4 :
a) Wir berechnen mit Hilfe der Gegenwahrscheinlichkeit (MAE3, Satz 8, 1.) sowie
mit der Tabelle im Kap. 1.3.5 der Vorlesung:
Z5
“P (X > 5)” = 1 − “P (X ≤ 5)” = 1 − FX (5) = 1 −
λe−λx dx
(23)
0
= 1 − −e
= e
−λx
5
= 1 + e−λx 5 = 1 + e−5λ − 1
0
0
−5λ !
= 0.05.
(24)
(25)
Aufgelöst nach λ erhalten wir λ = − 15 ln(0.05) ' 0.60.
b) Wie vorher berechnen wir
Zq
“P (X > q)” = 1 − “P (X ≤ q)” = 1 − FX (q) = 1 −
= 1 − −e
−λx
λe−λx dx
0
q
= 1 + e−λx q = 1 + e−λq − 1
0
0
!
= e−λq = p
(26)
(27)
(28)
Aufgelöst nach λ erhalten wir λ = − 1q ln(p) > 0.
c) Mit der Gegenwahrscheinlichkeit berechnen wir
0.5 = “P (X ≤ m)” = 1 − “P (X > m)”
4
⇒
“P (X > m)” = 1 − 0.5 = 0.5.
(29)
Wir derselben Rechnung wie in Aufgabe 4b erhalten wir
!
“P (X > m)” = · · · = e−λm = 0.5.
(30)
Nach m aufgelöst erhalten wir den Median der Exponentialverteilung:
1
1
1
ln(2)
m = − ln
= − (− ln(2)) =
> 0.
λ
2
λ
λ
(31)
λ = 0.5, m = 1.4
1
0.4
0.8
0.3
0.6
X
fX(x)
F (x)
0.5
0.2
0.4
0.1
0.2
0
−5
0
5
10
0
−5
x
0
5
x
Vorlesungswebseite: http://home.zhaw.ch/~kirs/MAE4
5
10