Klassenarbeit Physik 10

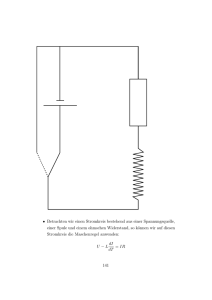
Hertzsche Wellen – Lösungen (Angaben ohne Gewähr!)
1. Erkläre die Wirkungsweise eines elektromagnetischen Schwingkreises!
Der Kondensator ist vollständig geladen (Ausgangszustand). Er beginnt, sich über die Spule zu
entladen, dabei steigt in der Spule die Stromstärke und damit auch das Magnetfeld. Durch
das sich ändernde Magnetfeld wird in der Spule eine Spannung induziert (Selbstinduktion).
Der Induktionsstrom behindert laut Lenzscher Regel das Ansteigen der Stromstärke (Ursache
der Entstehung des Induktionsstromes). Die Stromstärke erreicht ihren Maximalwert, so dass
der Kondensator vollständig entladen ist. Die Stromstärke (durch die Spule) sinkt ab. Dies
wird durch das sich dabei ändernde Magnetfeld und der daraus resultierenden
Selbstinduktionsspannung behindert, so dass der Strom weiter fließt und den Kondensator
entgegengesetzt auflädt. Der Vorgang endet, wenn der Kondensator vollständig geladen ist.
Der Vorgang beginnt mit umgekehrtem Vorzeichen neu.
2. Zeichne den Aufbau einer Meissnerschen Rückkopplungsschaltung!
siehe Hefter
3. Nenne die Eigenschaften der Hertzschen Wellen!
Hertzsche Wellen werden von Nichtleitern hindurchgelassen und an elektrischen Leitern
reflektiert. (Es gilt dann das Reflexionsgesetz.)
Hertzsche Wellen breiten sich mit Lichtgeschwindigkeit aus. Es gilt: c = λ ∙ f
Hertzsche Wellen werden beim Übergang von einem in einen anderen Stoff gebrochen.
Hertzsche Wellen werden gebeugt und können sich überlagern (Interferenz).
4. Erkläre das Verhalten einer Spule im Wechselstromkreis gegenüber dem Gleichstromkreis!
R~ > R Im Wechselstromkreis kommt zum ohmschen der induktive Widerstand hinzu.
Durch den Wechselstrom ändert sich in der Spule ständig das Magnetfeld. Dadurch wird
ständig eine Selbstinduktionsspannung erzeugt, so dass der dabei entstehende
Induktionsstrom laut Lenzscher Regel der Ursache seiner Entstehung (Wechselstrom)
entgegenwirkt. Der Widerstand ist also größer.
5. Begründe, warum ein und derselbe UKW-Sender an zwei verschiedenen Orten mit
unterschiedlichen Frequenzen sendet!
Die Sender könnten sich überlagern, so dass es zu Verstärkungen oder Auslöschungen
kommen würde.
6. Berechne die Wellenlänge eines UKW-Senders mit 100,2 MHz!
𝑘𝑚
geg.: f = 100,2 MHz, c = 299711 𝑠
ges.: λ
Lösg.: c = λ ∙ f
|: f
𝑐
λ=𝑓
299711000
𝑚
𝑠
λ = 100,2 ∙ 106 𝑠−1
λ = 2,99 m
7. Bei der Flugüberwachung wird ein Radarimpuls nach 2,6 ms wieder empfangen.
Berechne, wie weit das Flugzeug von der Radarstation entfernt ist!
𝑘𝑚
s = v ∙ t = 299711 𝑠 ∙ 0,0013 s = 389,62 km
8. Gib die Abhängigkeit der Stromstärke von der Frequenz in einer Spule an! Erkläre diese
Abhängigkeit!
Je größer die Frequenz, desto kleiner die Stromstärke.
Mit steigender Frequenz ändert sich in der Spule das Magnetfeld schneller, so dass die
Selbstinduktionsspannung größer wird. Der dadurch induzierte Strom behindert damit nach
Lenzscher Regel stärker die Ursache seiner Entstehung, also die ursprüngliche
Wechselstromstärke.
9. Gib die Abhängigkeit der Stromstärke von der Frequenz in einem Kondensator an!
Je größer die Frequenz, desto größer die Stromstärke.
10. Zeichne den Aufbau (Schaltplan) eines einfachen Hochpasses für Lautsprecher!
Lautsprecher in Reihe mit einem Kondensator
11. Zeichne den Aufbau (Schaltplan) eines einfachen Tiefpasses für Lautsprecher!
Lautsprecher in Reihe mit einer Spule
12. In einem Schwingkreis sind eine Spule mit einer Induktivität von 0,7 H und ein Kondensator
mit einer Kapazität von 0,4 μF vorhanden. Berechne die Eigenfrequenz des Schwingkreises!
f = 300,77 Hz
13. Ein Schwingkreis mit einer Eigenfrequenz von 200 Hz enthält einen Kondensator mit einer
Kapazität von 0,2 μF. Berechne die Induktivität, die die Spule besitzt!
geg.: f = 200 Hz, C = 0,2 μF
ges.: L
1
Lösg.: T = 2π√𝐿 ∙ 𝐶 |()²
T = 𝑓 = 0,005 s
T²= 4π² ∙ L ∙ C
L=
L=
|:(4π² ∙ C)
𝑇2
4𝜋2 ∙𝐶
(0,005 𝑠)²
4𝜋2 ∙ 0,2 ∙ 10−6 𝐹
L = 3,17 H
14. Ein Schwingkreis mit einer Eigenfrequenz von 440 Hz enthält eine Spule mit einer Induktivität
von 0,6 H. Berechne die Kapazität des Kondensators im Schwingkreis!
C = 0,22 μF
15. Im Schwingkreis mit einer bestimmten Eigenfrequenz wird die Kapazität des Kondensators
verdoppelt. Wie muss sich die Induktivität der Spule ändern, damit die Periodendauer T des
Schwingkreises auf das Dreifache steigt? Begründe!
Induktivität muss auf das 4,5-fache steigen.
Begründung: Damit die Periodendauer ( T = 2π∙ √𝐿 ∙ 𝐶 ) auf das Dreifache steigt, muss der
Ausdruck unter der Wurzel auf das Neunfache steigen. Da die Kapazität sich verdoppelt,
muss die Induktivität auf das 4,5-fache steigen, denn 2 x 4,5 = 9.