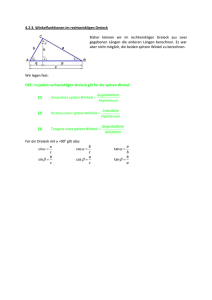
4.5.4. Sinus, Kosinus und Tangens

4.5.4. Sinus, Kosinus und Tangens
Auch sie gelten nur rechtwinkeligen Dreieck S.88. Bevor wir weitermachen, müssen wir
wieder neue Begriffe einführen, nämlich die Begriffe Ankathete und Gegenkathete. Beides
sind Katheten, schließen also den rechten Winkel ein. Um den Unterschied deutlich
herauszuarbeiten, brauchen wir wieder eine Skizze.
Die Seite c ist die Hypotenuse, da sie gegenüber vom rechten Winkel liegt und auch die
längste Seite im Dreieck ist. Die Seiten a und b sind also die Katheten. Welche ist aber nun
die Ankathete und welches ist die Gegenkathete. Nun, dass kommt auf die Auswahl des
Winkels an. Vom Winkel Alpha () aus gesehen ist b die Ankathete, da die Kathete b am
Winkel  anliegt, und a die Gegenkathete, da die Kathete a dem Winkel  gegenüberliegt.
Von Winkel Beta () ausgesehen ist a die Ankathete, da die Kathete a am Winkel  anliegt,
während b die Gegenkathete ist, da die Kathete b gegenüber vom Winkel  liegt. Vom
Winkel Gamma () aus gesehen gibt es nur Ankatheten und deshalb kann man von dem
Winkel  auch nicht den Sinus, Kosinus und Tangens aufstellen.
Wir merken uns: Die Ankathete liegt am Winkel dran, während die Gegenkathete dem
Winkel gegenüberliegt.
Bestimme doch mal bei den folgenden Dreiecken jeweils Ankathete (AK) und Gegenkathete
(GK), wobei die Sicht vom rechten Winkel aus nicht interessiert.
Dreieck 1:
Dreieck 2:
Dreieck 3:
Von Alpha aus gesehen
Von Beta aus gesehen
Von Beta aus gesehen
Von Gamma aus gesehen
Von Alpha aus gesehen
Von Gamma aus gesehen
(AK = b und GK = a)
(AK = a und GK = b)
(AK = c und GK = b)
(AK = b und GK = c)
(AK = c und GK = a)
(AK = a und GK = c)
Nachdem nun klar sein sollte, was Ankathete bzw. Gegenkathete ist, können wir Sinus,
Kosinus und Tangens gemäß folgender Regel aufstellen. Der Kotangens ist nur der
Vollständigkeit halber mit aufgeführt. Den brauchst du dir nicht zu merken.
Sinus 
Gegenkathete
Hypotenuse
Cosinus =
Ankathete
Hypothenuse
Tangens =
Gegenkathete
Sinus

Ankathete
Cosinus
Cotangens =
1
Cosinus
Ankathete


Tangens
Sinus
Gegenkathete
In der praktischen Anwendung kann man mit Sinus, Kosinus und Tangens Winkel bzw.
Seitenlängen berechnen dazu jeweils ein Beispiel:
Von dem folgenden rechtwinkeligen Dreieck ist folgendes bekannt:
a = 5 cm, c = 10 cm und  = 90 Grad. Bestimme mit Hilfe von Sinus bzw. Kosinus den
Winkel  und die Länge der Seite b.
Um von dem Sinuswert auf den Winkel zu kommen,
Gegenkathete a
5
sin  
 
 0,5 muss man arcus sinus bzw. sin -1 im Taschenrechner
Hypotenuse
c 10
eingeben. Diese Funktion findet man normalerweise mit
sin   0,5

  30
der Shift - Taste oder der 2nd - Taste und dem Sinus.
Ankathete
b
 Seitenvertauschen  c
Hypotenuse c
b  cos( )  c  cos 30  10  0,866  10  8,66
cos  