Vorbereitung Franck-Hertz-Versuch

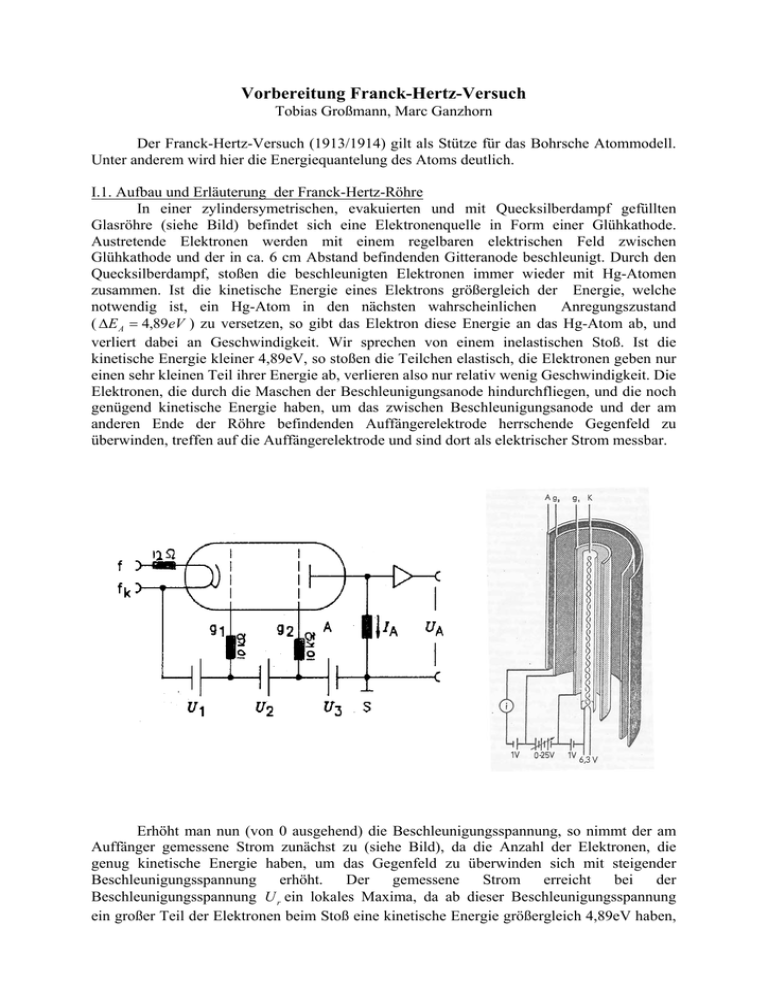
Vorbereitung Franck-Hertz-Versuch
Tobias Großmann, Marc Ganzhorn
Der Franck-Hertz-Versuch (1913/1914) gilt als Stütze für das Bohrsche Atommodell.
Unter anderem wird hier die Energiequantelung des Atoms deutlich.
I.1. Aufbau und Erläuterung der Franck-Hertz-Röhre
In einer zylindersymetrischen, evakuierten und mit Quecksilberdampf gefüllten
Glasröhre (siehe Bild) befindet sich eine Elektronenquelle in Form einer Glühkathode.
Austretende Elektronen werden mit einem regelbaren elektrischen Feld zwischen
Glühkathode und der in ca. 6 cm Abstand befindenden Gitteranode beschleunigt. Durch den
Quecksilberdampf, stoßen die beschleunigten Elektronen immer wieder mit Hg-Atomen
zusammen. Ist die kinetische Energie eines Elektrons größergleich der Energie, welche
notwendig ist, ein Hg-Atom in den nächsten wahrscheinlichen
Anregungszustand
( ΔE A = 4,89eV ) zu versetzen, so gibt das Elektron diese Energie an das Hg-Atom ab, und
verliert dabei an Geschwindigkeit. Wir sprechen von einem inelastischen Stoß. Ist die
kinetische Energie kleiner 4,89eV, so stoßen die Teilchen elastisch, die Elektronen geben nur
einen sehr kleinen Teil ihrer Energie ab, verlieren also nur relativ wenig Geschwindigkeit. Die
Elektronen, die durch die Maschen der Beschleunigungsanode hindurchfliegen, und die noch
genügend kinetische Energie haben, um das zwischen Beschleunigungsanode und der am
anderen Ende der Röhre befindenden Auffängerelektrode herrschende Gegenfeld zu
überwinden, treffen auf die Auffängerelektrode und sind dort als elektrischer Strom messbar.
Erhöht man nun (von 0 ausgehend) die Beschleunigungsspannung, so nimmt der am
Auffänger gemessene Strom zunächst zu (siehe Bild), da die Anzahl der Elektronen, die
genug kinetische Energie haben, um das Gegenfeld zu überwinden sich mit steigender
Beschleunigungsspannung
erhöht.
Der
gemessene
Strom
erreicht
bei
der
Beschleunigungsspannung U r ein lokales Maxima, da ab dieser Beschleunigungsspannung
ein großer Teil der Elektronen beim Stoß eine kinetische Energie größergleich 4,89eV haben,
so dass der Stoß inelastisch verläuft. Dadurch werden diese
Elektronen stark abgebremst, so dass sie das Gegenfeld
nicht überwinden können, und die Auffangelektrode nicht
erreichen. Erhöht man die Beschleunigungsspannung weiter,
nimmt die Anzahl der Elektronen, die nach dem
inelastischen Stoß genügend kinetische Energie haben das
Gegenfeld zu überwinden, zu. Die inelastischen Stöße
können auch mehrfach hintereinander passieren, so dass
auch bei Beschleunigungsspannungen von 2 U r , 3 U r , 4 U r ,
n U r lokale Maxima vorliegen. Trägt man nun den
gemessenen Strom über der Beschleunigungsspannung auf,
so erhält man ein markantes Stufenförmiges Schaubild
(siehe Bild), mit lokalen Maximas alle 4,89eV.
I.2. Aufnahme der Franck-Hertz-Kurve bei verschiedenen Parametern
Zunächst wird die Kathodenheizung auf Betriebstemperatur gebracht und
anschliessend mit der Ofenheizung die Röhre auf ca. 170°C vorgeheizt. Es sollen dann mittels
Oszilloskop die günstigsten Betriebsbedingungen (Kathodenheizung, Spannung am
Raumladungsgitter, Gegenspannung) festgestellt werden und anschliessend mit dem X-Y
Schreiber die „optimale Franck-Hertz-Kurve“ bei verschiedenen Röhrentemperaturen (120°C
bis 170°C) aufgenommen werden (Strom an der Auffängerelektrode gegen
Beschleunigungsspannung). Man erwartet unterschiedliche Kurven bei verschiedenen
Temperaturen, da die Stosswahrscheinlichkeit der Atome von der Temperatur in der Röhre
abhängt.
Es soll dann hierraus die Energie der niedrigsten beobachtbaren Anregung von
Quecksilber bestimmt werden. Zudem soll dann noch die Kontaktspannung zwischen Kathode
und Anode bestimmt werden.
I.3. Anodenstromkurve
Es soll nun der Anodenstrom als Funktion der Beschleunigungsspannung bei einer
Röhrentemperatur gemessen werden. Es soll folgender Zusammenhang verifiziert werden:
3
I Anode ≈ λ ⋅U 2
mit
λ=
k ⋅T
p ⋅ 8 ⋅10−16 cm 2
(mittlere freie Weglänge)
Trägt man den Anodenstrom über der Beschleunigungsspannung auf, so kann man an diesem
Graphen kein „Franck-Hertz Verhalten“ erkennen, da an der Anode wesentlich mehr
Elektronen als an der Auffängerelektrode absorbiert werden, so dass die durch das „FranckHertz Verhalten“ entstehende Änderung bei einem großen Elektronenstrom nicht messbar ist.
I.4. Ionisierungsenergie
Es soll hier der Anodenstrom als Funktion der Anodenspannung ermittelt werden. Für
diesen Versuch ist eine geringe Atomdichte von Vorteil. Es genügt daher eine Temperatur
von 120°C in der Röhre. Zusätzlich reduziert man die Glühspannung um ständige
Gasentladungen zu vermeiden. Um Hg-Atome zu ionisieren benötigt man eine kinetische
Energie von min. 10,44 eV. Es entstehen also positive Ionen in der Röhre welche in Richtung
Kathode wandern und somit die Raumladung in Kathodennähe herabsetzen. Zudem bewirken
sie ab der Ionisierungsenergie einen rechten steilen Anstieg Anodenstroms. Sie treten auch im
Anode-Auffängerraum auf und bewirken dort einen Strom entgegengesetzt zum
Elektronenstrom.
I.5. Emissionslinien
Bei brennender Gasentladung, sollen nun mit einem Spektroskop die Spektrallinien
des, durch die Rekombination der positiven Hg-Ionen und freien Elektronen, emittierten
Lichtes gemessen werden.
Der Spannungsabfall am Widerstand in der Anodenleitung ist so klein (weil nur sehr
kleine Ströme fließen), dass er vernachlässigt werden kann.
II Bestimmung der Energie für die nächsthöhere Anregung
Bisher wurden fast ausschließlich niedrige Anregungsniveaus beobachtet, da es am
wahrscheinlichsten ist, dass ein beschleunigtes Elektron bei einem Stoß mit einem Hg-Atom
4,89eV überträgt. Die Wahrscheinlichkeit eines solchen Stoßes ist proportional zur
Beschleunigungsstrecke und reziprokproportional zur mittleren freien Weglänge. Daher muss,
um höhere Anregungsniveaus zu ermöglichen, die Beschleunigungsstrecke verkleinert werden
und der Gasdruck gering gemacht werden (durch Senken der Temperatur). Hierzu wird die
Apparatur geändert, es wird nun die Beschleunigungsspannung zwischen Kathode und
Raumladungsgitter angelegt. Da die Temperatur reduziert wird, muss auch der
Kathodenheizstrom verringert werden, da es sonst leicht zu Gasentladungen kommt. Im
Schaubild erkennt man nun keine periodischen Peaks mehr, sondern Linearkombinationen aus
den beiden wahrscheinlichsten Anregungsniveaus (4,9eV und 6,7eV).
III Franck-Hertz Kurve für Neon
In diesem Versuch, soll die Franck-Hertz Kurve für Neon bestimmt werden, da bei
Neon die Anregungsniveaus aber sehr nahe beieinander liegen, kann hier nur eine mittlere
Anregungsenergie bestimmt werden. Da Neon bei Raumtemperatur als Gas vorliegt, und da
die mittlere Freie Weglänge unabhängig von der Temperatur ist,
n ⋅R ⋅T
k ⋅T
und λ =
p⋅σ
V
muss die Röhre nicht geheizt werden.
mit p =
folgt:
λ=
k⋅V
n ⋅R ⋅σ
Wir erwarten bei ab einer bestimmten Beschleunigungsspannung U Neon , die Elektronen
genügend kinetische Energie besitzen, um die Neon Atome anzuregen, dies wird als rote
Leuchterscheinung nahe der Anode sichtbar. Diese Leuchterscheinung wird bei steigender
Beschleunigungsspannung zur Kathode wandern, bis bei 2 U Neon , wenn die Elektronen
genügend kinetische Energie für eine zweite Anregung haben, eine weitere
Leuchterscheinung an der Kathode sichtbar wird.