Waermelehre-2-7

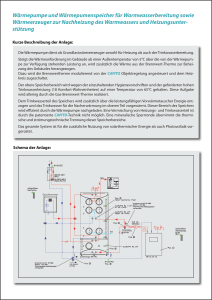
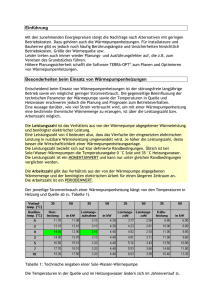
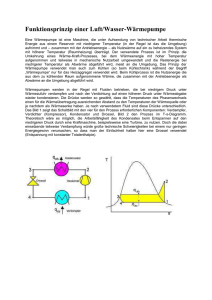
Finn Lorbeer & Arndt Quer
Physikalisches Praktikum für Anfänger – Teil 1
Gruppe 2 - Wärmelehre
2.7 Wirkungsgrad einer Wärmepumpe
Motivation:
Die Wärmepumpe ist eine Maschiene, die Wärme von einem niedrigen Temperaturniveau unter
Aufwand von Arbeit auf ein höheres Temperaturniveau transportiert.
Wir wollen in dem Versuch die Leistungzahl der Pumpe untersuchen unter verschiedenen
Vorraussetzungen.
Aufbau:
Gemäß der Abbildung sind die Geräte angeschlossen. Die Wärmepumpe entzieht dem linken
Wasserreservoir (welches in der Abb. mit T1 gekennzeichnet ist) Wärme pro Zeit. Dem Rechten
wird Wärme hinzugeführt. Beide Reservoirs sind an ein Temperaturmessgerät angeschlossen.
Zudem wird die Leistung der Wärmepumpe abgelesen.
Es gilt für die aufgenommene Wärmemenge des Wasserreservoir gekennzeichnet mit T2 pro
Zeitintervall:
Q2  T 2
=
⋅m⋅c H O
t
t
Q
Die Leistungszahl ε der Wärmepumpe ist definiert als =
.
P⋅ t
ε ist eine Maß von der transportierten Energie pro aufgewendeter Energieeinheit. P ist die Leistung
der Wärmepumpe.
2
Nun messen wir alle halbe Minute die Temperaturen in den Wasserbädern, so wie die derzeitige
Leitung der Pumpe. (→ Messung)
Wir erwarten dabei eine gegenläufige Veränderung der Temperaturen in den Wasserreservoirs.
Bestimmung von  :
Graphische Bestimmung mit dem Differenzenquotient:
mit Δt=3min.
Die Berechnung von ε:
T 2⋅m⋅c H O
=
P⋅ t
2
t / min
T2(t) / °C
T2(t+Δt) / °C
 /W
P
ΔT=T2 -T1
ε
0
3
6
9
12
Den Fehler des Messgeräts, müssen wir leider auf 0,4°C setzen, da im Digitaldisplay eine Diode
defekt ist und man im Zweifelsfall eine 5 für eine 9 gehalten werden könnte. Damit ist ΔT=0,3°C.
Einen Fehler in der Zeit gibt es auch, der wird bei 5 Sekunden liegen, da man eigentlich an einem
Zeitpunkt jeweils 3 Werte ablesen muss. Mit Umstellen des Messgeräts auf die andere Temperatur,
sind da sicher mal ein Zeitraum von Δt=5s entstanden.
Leider empfinden wir diesen Fehler nun sehr groß: 5Sekunden in einem 30Sekundeninterval (17%)
und 0,3°C bei Temperaturveränderungen pro Intervall von teilweise nur 0,1°C (300%).
Jedoch liegt, wie beschrieben, leider der Fehler in der Apparatur, so dass wir keine Möglichkeit
sahen, ihn zu verringern.
Nun führen wir den Versuch nochmals durch, halten die Wassertemperatur im Behälter 1 aber
möglichst konstant.
Bestimmung von  :
Graphische Bestimmung mit dem Differenzenquotient:
mit Δt=3min.
Die Berechnung von ε:
T 2⋅m⋅c H O
=
P⋅ t
2
t / min
T2(t) / °C
T2(t+Δt) / °C
 /W
P
ΔT=T2 -T1
ε
0
3
6
9
12
Fehler: (siehe Fehler Messung 1) zudem kommt noch hinzu, dass (wie man an den Werten erkennt),
wir es nicht optimal geschafft haben, die Temperatur 1 konstant zu halten. Sie schwankt um fast
3,5°C.
Auswertung:
Wie man sieht, ist die Leistungszahl ε in der zweiten Messung, in der ein Reservoir thermisch
konstant gehalten wird größer (außer dem Fall 0=0). Also ist das Verhältnis von abgegebener
Leistung zur elektrischen Antriebsleistung größer. Auch das darf man erwarten.
Betrachten wir hierfür als Erklärung die Kurven T über t. Hier sehen wir eine schnellere
Veränderung für Wasserbäder mit geringer Temperaturdifferenz. Je größer die
Temperaturdifferenz wird, desto mehr nähern sich die die Enden des Graphen einer
Parallelen der Zeit-Achse an.
Betrachten wir nun die Kurve des Diagramms für die 2. Messung und haben im Hinterkopf,
dass die Leistung annähernd konstant ist, dann sehen wir, dass mit größerer
Temperaturdifferenz auch die Temperaturveränderung kleiner wird.
Zurück zum Ausgangsgedanken: Wir halten die Temperaturdifferenz in der grünen Kurve geringer,
also steigt die Leistungszahl schneller.
Wenn wir die Formeln betrachten, dann sieht man, dass ΔT in der ersten Messung immer größer ist,
als in der 2. Messung – Da T1 ja im Gegensatz zur 2. Messung sinkt.
Dann erkennen wir, dass ε explizit nur eine Funktion ist, von ΔT2. Der Rest sind Konstanten.
Da die bei gleicher Leistungszahl nun aber ΔT in der ersten Messung größer ist, ist die Gerade
flacher.