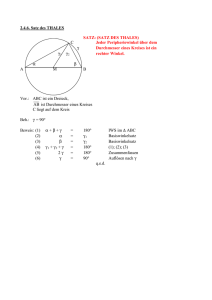
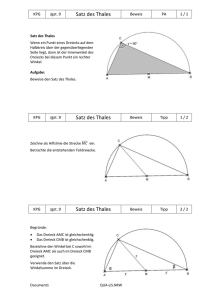
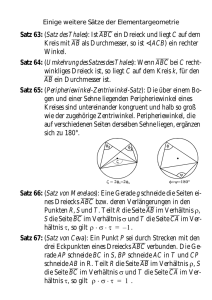
Analogisieren – Vom Satz des Thales zum Umfangswinkelsatz

Analogisieren –
Vom Satz des Thales zum Umfangswinkelsatz
Der Satz des Thales
Liegt ein Punkt C auf dem Kreis über einer Strecke [AB], so ist das Dreieck ABC
rechtwinklig.
Beweis:
(1) MA = MC und MB = MC (Voraussetzung: A, B und C liegen auf Kreis um M )
α1 = α 2 und β1 = β 2
(2)
(1, BWS in + AMC und + BMC )
2α 2 + 2β 2 = 180°
(3)
(2, IWS in + ABC )
(4)
2 (α 2 + β 2 ) = 180°
(3)
(5)
(4)
α 2 + β 2 = 90°
Thales
Thales als Sonderfall
C
C
α2 β 2
α1
A
Umfangswinkelsatz
C
α2 β 2
M
α1
β1
γ1
B
α2
M
μ
β2
β1
γ2
M
B
α1
A
γ1
μ
β1
γ2
A
B
Verallgemeinerung zum Umfangswinkelsatz
Beobachtung: Liegt C auf dem Kreisbogen BA mit Mittelpunkt M, so hat der Winkel ACB
unabhängig von der genauen Lage von C nicht mehr notwendig 90° aber zumindest stets
denselben Wert.
Versuch eines analogen Beweises:
Der Beweis lässt sich fasst direkt vom Beweis des Thalessatzes übernehmen. Als einzige
Modifikation ist es notwendig, das zusätzliche gleichschenklige Dreieck mit den
Basiswinkeln γ1 und γ1 zu berücksichtigen. Mit Beweisschritt (6) könnte der Beweis beendet
werden. Die Ersetzung von 90° − γ durch μ / 2 in (6) lässt sich durch Analogisieren nicht
mehr entdecken.
MA = MC und MB = MC
(1)
(Voraussetzung)
(2) α1 = α 2 , β1 = β 2 und γ 1 = γ 2 (1, BWS in + AMC , + BMC und + BMA)
(3)
2α 2 + 2β 2 + 2γ = 180°
(2, IWS in + ABC )
(4)
2 (α 2 + β 2 + 2γ ) = 180°
(3)
(5)
(4)
α 2 + β 2 + γ = 90°
(6)
°−γ
(5)
α 2 + β 2 = 90
μ /2