docx
Werbung

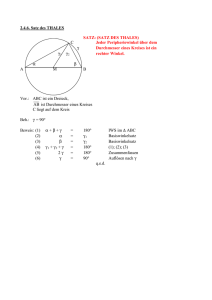
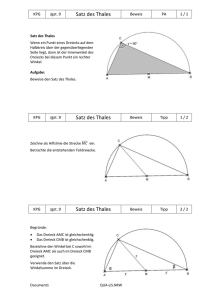
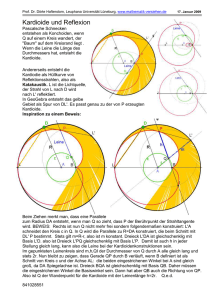
4.1.6. Satz des THALES 1 A C SATZ: (SATZ DES THALES) Jeder Peripheriewinkel über dem Durchmesser eines Kreises ist ein rechter Winkel. 2 M B Beweis: Der Beweis wird geführt für ein gleichschenkliges Dreieck. Das ist zulässig, weil jeder andere Peripheriewinkel über dem gleichen Bogen gleich groß ist. (Peripheriewinkelsatz) Vor.: ABC ist ein gleichschenkliges Dreieck, AB ist Durchmesser eines Kreises C liegt auf dem Kreis Beh.: = 90° Beweis: (1) (2) (3) (4) (5) (6) (7) (8) (9) + + 1 1 + + 2 2 1 + 2 = = = = = = = = = IWS im AMC Eigenschaft der Höhe AMC ist gleichschenklig (1); (2); (3) IWS im BMC Eigenschaft der Höhe BMC ist gleichschenklig (5); (6); (7) (4); (8) 180° 90° 1 45° 180° 90° 2 45° 90° q.e.d. Die Umkehrung des Thalessatzes ist eine wahre Aussage.