Beweis des Mittelpunktwinkelsatzes

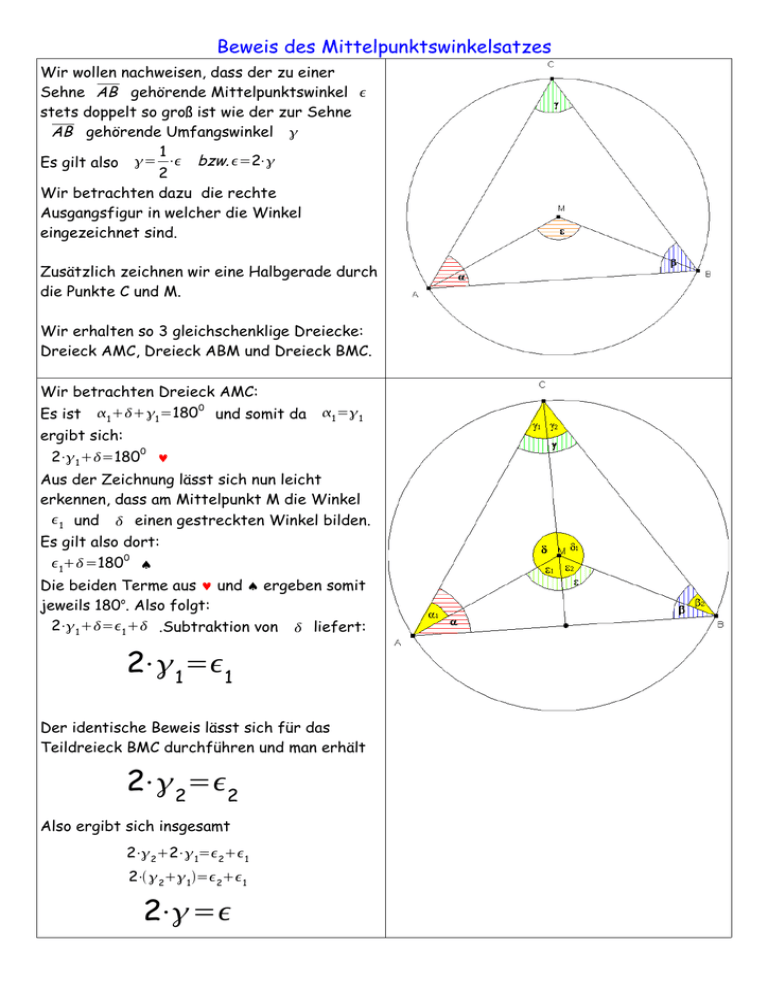
Beweis des Mittelpunktswinkelsatzes
Wir wollen nachweisen, dass der zu einer
Sehne AB gehörende Mittelpunktswinkel 
stets doppelt so groß ist wie der zur Sehne
AB gehörende Umfangswinkel 
1
Es gilt also = ⋅ bzw. =2⋅
2
Wir betrachten dazu die rechte
Ausgangsfigur in welcher die Winkel
eingezeichnet sind.
Zusätzlich zeichnen wir eine Halbgerade durch
die Punkte C und M.
Wir erhalten so 3 gleichschenklige Dreiecke:
Dreieck AMC, Dreieck ABM und Dreieck BMC.
Wir betrachten Dreieck AMC:
0
Es ist 1 1 =180 und somit da
1 =1
ergibt sich:
0
2⋅1 =180 ♥
Aus der Zeichnung lässt sich nun leicht
erkennen, dass am Mittelpunkt M die Winkel
1 und  einen gestreckten Winkel bilden.
Es gilt also dort:
0
1=180 ♠
Die beiden Terme aus ♥ und ♠ ergeben somit
jeweils 180o. Also folgt:
2⋅1 =1  .Subtraktion von  liefert:
2⋅1 =1
Der identische Beweis lässt sich für das
Teildreieck BMC durchführen und man erhält
2⋅2 =2
Also ergibt sich insgesamt
2⋅22⋅1=21
2⋅ 21 =21
2⋅=