Mv 044-050-Dreiecke
Werbung

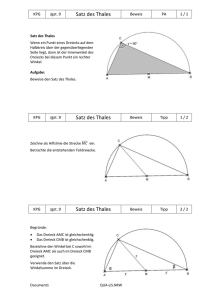
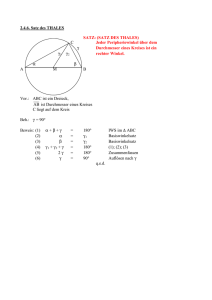
▲ DREIECKE Satz des Thales Von der Kreislinie aus sieht man den zugehörigen Durchmesser unter einem rechten Winkel. Inhalt ✖ Experimentieren und Diese elementare Aussage wird (ohne fundierten Beleg) mit Winkel messen dem ionischen Philosophen Thales von Milet (ca. 620 bis ✖ Vermutung und ca. 540 v. Chr.) in Verbindung gebracht und nimmt einen Beweisstrategie festen Platz in vielen Lehrplänen ein. ✖ Beweis Die Person des Thales sollte aber auch zu kulturhistorischen ✖ Umkehrung des Satzes Betrachtungen anregen. Literatur hierzu findet sich beispielsweise in den beiden Büchern: P. Baptist: Pythagoras und kein Ende? – Klett 1997, S. 70 ff. Zeitrahmen H. Heuser: Als die Götter lachen lernten – Piper 1992, S. 43 ff. 1 Stunde Material ✖ Geodreieck ✖ Zirkel ✖ Lerntagebuch 45 SATZ DES THALES Experimentieren Die Schüler sollen durch Ausprobieren eigenständig zu einer Vermutung gelangen, wobei sie in ihrem Lerntagebuch zusätzlich eine Skizze anfertigen und ihre Überlegungen aufschreiben. Das Arbeitsblatt zeigt das Dreieck ABC mit Umkreis, die Seite [AB] ist Durchmesser des Kreises. Rechts neben der Figur sind die Größen der Innenwinkel des Dreiecks angezeigt. Der Eckpunkt C lässt sich mit der Maus auf der Kreislinie bewegen. Dadurch entstehen neue Dreiecke. Die Größen der Innenwinkel bei A und B ändern sich, der Winkel bei C misst immer 90°. 46 ▲ ▲ SATZ DES THALES Vermutung und Beweisstrategie Das zweite Blatt ermöglicht einen Vergleich der eigenen Vermutung mit der Formulierung auf dem Arbeitsblatt. Anschließend sollen die Schüler eigenständig eine Begründung erarbeiten. Dazu wird die Strategie vorgegeben: Wähle eine geeignete Hilfslinie. Mit dem Mouseover-Effekt („Überstreichen“ der farblich hervorgehobenen Wörter mit der Maus) kann man diese Hilfslinie sichtbar machen. Hinter dem Tipp-Button verbergen sich zwei weitere Hinweise zum Beweis: „Gleichschenklige Dreiecke“ und „Winkelsumme im Dreieck“. 47 SATZ DES THALES Beweis Dieses Arbeitsblatt zeigt den vollständigen Beweis. Durch den MouseoverEffekt lassen sich die entscheidenden Teildreiecke farblich hervorheben. Dieses Blatt dient zur Kontrolle und Ergänzung der Beweisversuche der Schüler. Der Beweis des Satzes des Thales kann also auch im Unterrichtsgespräch oder im Rahmen eines Schülervortrages erarbeitet werden, wobei natürlich die Beweise bzw. Beweisversuche der Schüler entsprechend einbezogen werden sollen. 48 ▲ ▲ SATZ DES THALES Weiterführende Fragestellung Wie lautet die Umkehrung des Satzes des Thales? Hier sollen die Schüler die Umkehrung des Lehrsatzes zunächst formulieren. Anschließend sollen sie den Eckpunkt C des Dreiecks ABC so bewegen, dass das eingeblendete Winkelmaß für möglichst 90° beträgt. Die Spur des Punktes C wird dabei aufgezeichnet (Klicken auf das GEONE xT – Logo löscht die Spur). Einen Vergleich der selbst gezeichneten Spur mit dem Thaleskreis ermöglicht ein Klick auf den Button „Thaleskreis“. 49 SATZ DES THALES ERGEBNISBLATT ▲ Satz des Thales Ein Dreieck, dessen Ecken so auf einem Kreis liegen, dass eine Seite Durchmesser ist, besitzt einen rechten Winkel. Strategie Verwende eine geeignete Hilfslinie, hier [ CM ]. Beweis C α β A β = CBA = MCB ( ∆ BCM gleichschenklig ) β α M α = BAC = ACM ( ∆ AMC gleichschenklig ) B ACB = γ = α + β 180° = α β γ = γ γ ⇒ γ = 90° Historische Notiz Dieses Ergebnis wird Thales von Milet (ca. 620 - ca. 540 v.Chr.) zugeschrieben, aber diese Feststellung steht auf äußerst wackeligen Füßen. 50 © Friedrich Verlag GmbH 2004