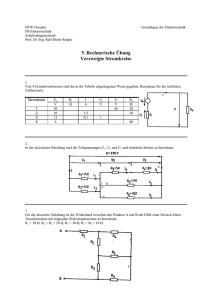
Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik
Werbung

Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 1 Aufgaben 05etu510 Inhaltsverzeichnis Teil 3 Kapitel 5: Wechselstromkreise Seite 5.1 5.2 5.3 5.4 5.5 5.6 5.6.1 5.6.2 5.7 5.7.1 5.7.2 5.7.3 5.7.4 5.8 5.9 5.9.1 5.9.2. 5.10 5.11 5.12 Wechselgrößen Wechselstromwiderstand Schaltungsberechnung im Zeitbereich Komplexe Schwingungsberechnung Komplexe Schaltungsberechnung Zeigerbilder, Ortskurven Zeigerbilder Ortskruven Spezielle Wechselstromschaltungen Passschaltungen 1, Ordnung Passschaltungen höherer Ordnung Schwingkreise Brückenschaltungen Wechselstromleistung Drehstromkreise Schaltungsberechnung Drehstromleistung Unsymmetrische Drehstromsysteme Schaltungen bei mehrfrequenter Erregung Vierpolschaltungen Lösungen 2 3 .3 .4 ..7 10 10 11 14 14 17 22 24 26 29 29 31 34 40 44 48 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 2 Aufgaben 05etu510 5.1 Wechselgrößen 5.1.01 ˆ ⋅ cos(ωt + ϕ ) . Gegeben ist die Wechselgröße x = X x a) Stellen Sie die Größe in einem Diagramm x = f(ωt) dar für folgende Nullphasenwinkel: 0; π/8; π/6; π/4; π/3; π/2; 2π/3; 5π/6; π; -π/6; -π/4; -π/3; -π/2; -2π/3; -π; b) Rechnen Sie die im Bogenmaß gegebenen Winkel in Grad um! 5.1.02 ˆ ⋅ cos(ωt + ϕ ) dar! Stellen Sie die nachstehenden Funktionen in der Form: x = X x ˆ ˆ b) x = X ⋅ sin(ωt + ϕ ) a) x = X ⋅ sin ωt 1 c) ˆ ⋅ sin ωt x3 = − X 2 d) x2 ˆ ⋅ sin(ωt + ϕ ) x4 = −X x4 5.1.03 Berechnen Sie Winkelfrequenz und Periodendauer folgender Frequenzen: 10 Hz; 50 Hz; 100 Hz; 300 Hz; 1 kHz; 10 kHz; 1 MHz; 100 MHz; 450 MHz 5.1.04 Stellen Sie die folgenden drei Spannungen in einem Diagramm dar! ˆ ⋅ cos ωt ˆ ⋅ cos(ωt − 2 π) ˆ ⋅ cos(ωt + 2 π) u1 = U u2 = U u3 = U 3 3 5.1.05 Gegeben ist der Strom i = 10A ⋅ cos(ωt + 41 π) mit f = 50 Hz. Berechnen Sie die Augenblickswerte für folgende Zeiten: t = 0; 5 ms; 10 ms; 12 ms; 20 ms; 50 ms! 5.1.06 Berechnen Sie die Zeiten im Zeitintervall 0 ≤ t ≤ 100 ms, zu denen der in Aufgabe 5.1.05 gegebene Strom den Augenblickswert a) ia =8 A; b) ib = 4 A; c) ic = -2 A hat! 5.1.07 Berechnen Sie den arithmetischen Mittelwert der Gleichspannung während einer Periode der Wechselspannung bei einer a) Einweggleichrichterschaltung b) Zweiweggleichrichterschaltung! 5.1.08 Berechnen Sie den Effektivwert folgender Spannungen und Ströme bei der Frequenz f = 50 Hz! a) u = 220V ⋅ cos(ωt + 31 π) b) u = 42V ⋅ cos(ωt + 61 π) c) i = 10A ⋅ cos(2ωt + 121 π) d) i = 1.41A ⋅ cos(2ωt − 21 π) Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 3 Aufgaben 05etu510 5.2 Wechselstromwiderstand 5.2.01 Berechnen Sie Wechselstromwiderstand und Wechselstromleitwert eines Kondensators der Kapazität C = 0.1 µF bei a) f = 50 Hz; b) f = 500 Hz c) f = 5 kHz! 5.2.02 Berechnen Sie Wechselstromwiderstand und Wechselstromleitwert einer Spule mit der Induktivität L = 0.5 H bei a) f = 50 Hz; b) f = 500 Hz c) f = 5 kHz! 5.2.03 Stellen Sie die Frequenzabhängigkeit der Wechselstromwiderstände und Wechselstromleitwerte von Kondensator und Spule qualitativ grafisch dar! 5.2.04 π Die Wechselspannung u = Û ⋅ cos(ωt + ) fällt ab über 4 a) einem ohmschen Widerstand R b) einem Kondensator mit der Kapazität C c) einer Spule mit der Induktivität L. Berechnen Sie die jeweils fließenden Ströme und stellen Sie den zeitlichen Verlauf der Spannung und der drei Ströme in einem Diagramm dar! 5.3 Schaltungsberechnung im Zeitbereich 5.3.01 Gegeben ist folgende Schaltung. i = 0.71A ⋅ cos ωt f = 50 Hz R = 100 Ω L = 1H i R L uR uL u Berechnen Sie die Spannungen uR, uL und u und stellen Sie die zeitlichen Verläufe des Stromes und der Spannungen in einem Diagramm dar! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 4 Aufgaben 05etu510 5.3.02 Gegeben ist folgende Schaltung. i = 0.86A ⋅ cos(ωt + 1.14) f = 50 Hz R = 150 Ω L = 0.8 H C = 5.5 µF R L uR uL C uC i u Berechnen Sie die Spannungen uR, uL, uC und u und stellen Sie die zeitlichen Verläufe des Stromes und der Spannungen in einem Diagramm dar! 5.4 KomplexeSchwingungsberechnung 5.4.01 Eine Glühlampe PN = 40W; UN = 230V ist mit einem Kondensator C = 2µF in Reihe geschaltet und an eine Wechselspannung U = 230V; f = 50 Hz gelegt. Berechnen Sie a) Widerstandsoperator der Reihenschaltung Z b) Stromzeiger I c) Zeiger der Spannungsfälle an Lampe UR und Kondensator UC d) Phasenverschiebung ϕ! 5.4.02 Die folgenden Schaltelemente sind in Reihe geschaltet. Berechnen Sie den Operator Z des Gesamtwiderstandes in Komponenten- und Exponentialdarstellung für f = 50 Hz! a) R = 200Ω L = 0.4H b) R = 150Ω L = 0.6H c) R = 500Ω C = 3µF d) R = 250Ω C = 6.5µF 5.4.03 Gegeben ist der Gesamtwiderstandsoperator der Reihenschaltung von Widerstand und Induktivität. a) Z = 8.5Ω 30o Z b) Z = 27Ω 63o Gegeben ist der Gesamtleitwertoperator der Parallelschaltung von Widerstand und Induktivität. c) Y = 9.5S −88o d) Y = 1.4S −65o Berechnen Sie jeweils Widerstand und Induktivität für f = 50Hz! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5 Aufgaben 05etu510 5.4.04 Berechnen Sie den Reihenersatzwiderstandsoperator eines Wechselstrommotors mit folgenden Werten: a) PN = 1.5kW; UN = 230V; cos ϕ = 0.78; η = 0.9 b) PN = 3.0kW; UN = 230V; cos ϕ = 0.80; η = 0.91 5.4.05 Eine Drosselspule hat einen ohmschen Widerstand RL = 4Ω und nimmt bei U = 110V; f = 50Hz den Strom I = 4.5A auf. Berechnen Sie den Wert eines ohmschen Vorschaltwiderstandes RV, durch den bei gleicher Spannung der Strom auf 1.5A verringert wird. 5.4.06 Berechnen Sie den Gesamtwiderstandsoperator einer Drosselspule mit nachgeschaltetem Kondensator! R = 1500Ω; L = 0.6H; C = 5.5µF; f = 50Hz Bei welcher Frequenz wird der Operator reell? 5.4.07 Berechnen Sie Leitwert- und Widerstandsoperator folgender Parallelschaltungen in Komponenten- und Exponentialform für f = 50Hz! a) R = 250Ω; L = 0.6H; b) R = 19Ω; L = 5mH; c) R = 1000Ω; C = 1µF; d) R = 770Ω; C = 0.5µF; C = 5µF; e) R = 800Ω; L = 1H; C = 4.5µF; f) R = 200Ω; L = 0.8H; 5.4.08 Parallel zu einem Widerstand R = 65Ω soll ein Kondensator geschaltet werden, so dass die Resistanz des Gesamtoperators bei f = 50Hz 40Ω beträgt! Berechnen Sie die Kapazität des Kondensators! 5.4.09 Parallel zu einem Kondensator von C = 0.5µF soll ein ohmscher Widerstand geschaltet werden, so dass der Imaginärteil des Gesamtwiderstandsoperators bei f = 50Hz nur noch 6000Ω beträgt. Berechnen Sie den notwendigen ohmschen Widerstand! 5.4.10 Ein ohmscher Widerstand ist mit einer Reaktanz parallel geschaltet und hat eine Gesamtimpedanz von a) Z = (12 + j9)Ω b) Z = ( 3 + j8)Ω c) Z = (14 - j11)Ω An der Schaltung fällt die Spannung U = 60V; f = 50Hz ab. Berechnen Sie den Gesamtstrom und die Zweigströme! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 6 Aufgaben 05etu510 5.4.11 Berechnen Sie den komplexen Leitwert und daraus den tan ϕ als allgemeine Beziehung! a) Welchen Wert muss in dieser Schaltung der Widerstand R2 haben, damit die Nacheilung des Stromes gegenüber der Spannung gerade 45°beträgt? b) Stellen Sie die Widerstandsoperatoren der Schaltung und ihre Zusammenhänge grafisch in der komplexen Ebene dar! R1 L R2 5.4.12 a) Berechnen Sie für das angegebene Netzwerk den komplexen Leitwert und den Widerstand als allgemeine Beziehung! b) Bestimmen Sie die Frequenz, bei der die Impedanz rein reell wird! c) Stellen Sie das Ergebnis von b) in der komplexen Ebene grafisch dar! R L C 5.4.13 Die Schaltung wird an der Wechselspannung U = 230V; f = 50Hz betrieben. Berechnen Sie a) den komplexen Ersatzwiderstand b) den Gesamtstrom c) den Phasenwinkel d) die Kapazität der entsprechenden Ersatzreihenschaltung e) die Kapazität der entsprechenden Ersatzparallelschaltung R1 = 1000Ω; U = 230V; R2 = 2500Ω; f = 50Hz; C = 4µF R1 C R2 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 7 Aufgaben 05etu510 5.5 Komplexe Schaltungsberechnung 5.5.01 a) Berechnen Sie die Teilströme für die Klemmenspannung U = 60V; f = 50Hz! b) Zeichnen Sie ein maßstäbliches Zeigerbild der Spannungen undStröme! R1 R2 R3 XL XC = 5Ω = 3Ω = 30Ω = 4Ω = 8Ω R1 j XL -j XC R2 R3 5.5.02 a) Berechnen Sie alle Ströme und Spannungen sowie den Gesamtphasenwinkel für die Klemmenspannung U = 230V; f = 50Hz! b) Zeichnen Sie das maßstäbliche Zeigerbild aller Spannungen und Ströme! R1 R2 L1 R3 R4 = 4Ω = 5Ω = 20mH = 8Ω = 10Ω R2 L1 R1 R3 R4 5.5.03 Der Effektivwert des durch die Schaltung fließenden Stromes soll trotz Zu- bzw. Abschalten von R2 seine Größe nicht ändern! Berechnen Sie für diesen Fall R2! R2 R1 A jXL 5.5.04 a) Berechnen Sie den Wert der Kapazität C in der Schaltung, damit der Strom I mit der Spannung U in Phase liegt! b) Berechnen Sie die Ströme I, I1 und I2! c) Zeichnen Sie ein maßstäbliches Zeigerbild aller Spannungen und Ströme! L1 = 0.02H R1 = 10Ω L2 = 0.04H R2 = 15Ω U = 220V 0o f = 50 Hz i1 R1 L1 R2 L2 i i2 C Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 8 Aufgaben 05etu510 5.5.05 In der Schaltung sollen R2 und XL so bestimmt werden, dass Gesamtstrom und Klemmenspannung phasengleich werden! R1 = 4Ω; R1 -jXC XC = 2Ω jXL 5.5.06 Berechnen Sie in der Schaltung den Strom I2 durch den Widerstand R2 mittels: a) b) c) d) Stromteilerregel Spannungsteilerregel Zweigstromverfahren Zweipoltheorie R2 jXL I2 Uq -jXC R2 R1 Uq = 220V; R1 = 5Ω; R2 = 50Ω; XL = 10Ω; XC = 100Ω 5.5.07 Berechnen Sie den Strom durch R2 mit dem Knotenspannungsverfahren! R1 = 1Ω; R2 = 5Ω; XL = 20Ω; XC = 20Ω; Uq = 12V 5.5.08 U a) b) c) I2 R1 R2 Uq -jXC jXL = 100V; R1 = 10Ω; R2 = 20Ω; XC = 30Ω Berechnen Sie die Spannung U2! Zeichnen Sie ein maßstäbliches Zeigerbild aller Spannungen und Ströme! Geben Sie die Spannung u2 = f(t) (Zeitbereich) an! R1 U -jXC R2 U2 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.5.09 Uq1 = 12V; Uq2 = 12V/45° R1 = 5Ω; XL = 15Ω; R2 = 10Ω; XC = 30Ω a) Berechnen Sie mit Hilfe des Überlagerungssatzes den Strom durch XC! b) Berechnen Sie mit Hilfe des Zweipolverfahrens den Strom durch XC! 9 Aufgaben 05etu510 R1 jXL Uq1 5.5.10 Gegeben ist der aktive Zweipol. Uq = 12 V; R1 = 2Ω; XL = 10Ω R2 = 2Ω; a) Berechnen Sie die Elemente der Spannungsquellen-Ersatzschaltung! b) Berechnen Sie die Elemente der Stromquellen-Ersatzschaltung! R2 Uq2 R1 R2 Uq jXL 5.5.11 Berechnen Sie mit dem Zweipolverfahren den Strom durch R2! U = 220V; XL1 = 15Ω; XC = 30Ω; R1 = 5Ω; XL2 = 50Ω; R2 = 100Ω R1 U jXL2 jXL1 -jXC U0 R2 I2 IC -jXC Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.6 5.6.1 10 Aufgaben 05etu510 Zeigerbilder, Ortskurven Zeigerbilder Zeichnen Sie das qualitative Zeigerbild aller Ströme und Spannungen der Netzwerke in den Aufgaben 5.6.1.01 bis 5.6.1.05! 5.6.1.01 − jXC1 j XL R1 R2 − jXC2 5.6.1.02 j XL R1 − jXC R2 5.6.1.03 jXL2 R3 R1 jXL1 R2 5.6.1.04 R1 − jXC R2 j XL 5.6.1.05 R1 R2 − jXC j XL Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 11 Aufgaben 5.6.1.06 Berechnen Sie mit Hilfe eines Zeigerbildes alle Spannungen und Ströme! R1 = 10Ω R3 = 50Ω XC1 = 10Ω U = 100V R2 = 5Ω Xc = 50Ω XL=20Ω 05etu510 I1 R1 I2 − jXC1 I3 I4 U R3 − jXC jXL 5.6.1.07 Gegeben ist eine Reihenschaltung mit R = 50 Ω und L = 0.2 H bei f = 50 Hz. Bestimmen Sie unter Verwendung eines Zeigerbildes Y! (mZ = 10 Ω/cm) 5.6.1.08 Gegeben ist eine Parallelschaltung mit R = 100 Ω und L = 0.4 H bei f = 50 Hz. Bestimmen Sie Z unter Verwendung eines Zeigerbildes! (mZ = 20 Ω/cm) 5.6.1.09 Gegeben ist eine Parallelschaltung mit R = 60Ω und C = 50µF bei f = 50Hz (mZ = 10Ω/cm; r = 5cm) Bestimmen Sie grafisch Z! 5.6.1.10 Ein Widerstand R1 = 400Ω liegt in Reihe mit einem Kondensator XC1 = 700Ω. Berechnen Sie R2 und XC2 einer äquivalenten Parallelschaltung! 5.6.1.11 Ein Widerstand R1 = 400Ω liegt parallel zu einer Spule XL1 = 600Ω. Berechnen Sie R2 und XL2 einer äquivalenten Reihenschaltung! 5.6.2 Ortskurven 5.6.2.01 Zeichnen Sie Z(R1)! mZ = 20 Ω/cm; R = 20 Ω; C = 5 µF; R1 = (0 ... 80) Ω; f = 800 Hz R2 R C R1 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 12 Aufgaben 05etu510 5.6.2.02 Stellen Sie für die folgende Schaltung die Ortskurven dar! a) b) ZAB = f(R) ZAB = f(f) 1 jω C R A B 5.6.2.03 Beweisen Sie analytisch, dass die Inversion der Geraden A(p) = B + jpC einen Kreis durch den Koordinatenursprung ergibt! Bestimmen Sie den Mittelpunkt und den Radius! Hinweis: 1/A(p) = x + jy 5.6.2.04 Zeichnen Sie Z(XL1) und Y(XL1)! mZ = 5Ω/cm; r = 6cm; R = 15Ω; XL = 5Ω; XL1 = 0...10Ω 5.6.2.05 R L ω C a) b) = 1000Ω =1H = 1000s-1 = (5...1.25)µF jXL jXL1 R R C L Zeichnen Sie Z(C) und Y(C)! mZ = 200Ω/cm mY = 1 mS/2.5 cm Die Klemmenspannung beträgt U = 20V 0o . Zeichnen Sie I = f(C)! 5.6.2.06 R C R1 f = 16Ω; = 5µF; = ∞...40Ω; = 1000Hz Zeichnen Sie Z(R1) und Y(R1)! R − jXC R1 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 13 Aufgaben 05etu510 5.6.2.07 R = 40Ω XL = 25Ω C = 0.1µF...10µF ω = 8000s-1 a) Zeichnen Sie Z = f(C)! b) Die Klemmenspannung beträgt U = 42 V 0o . Zeichnen Sie I = f(C)! 5.6.2.08 f U RFe R1 R2’ XH Xσ a) b) c) = 50Hz = 230V 0o = 25.3Ω = 66.7mΩ = 117mΩ = 6.20Ω = 598mΩ j XL R − jXC I l2 I1 R1 I0 R'2 /s U jXσ RFe jXH Zeichnen Sie die Ortskurve des Stromes − I l2 = f(s) für 0 ≤ s ≤ ∞ ! Zeichnen Sie die Ortskurve des Stromes I 1 = f(s) für 0 ≤ s ≤ ∞ ! Stellen Sie I2 ⋅ cos ϕ2 = f(s) im Wertebereich 0 ≤ s ≤ 1 in einem Diagramm dar! 5.6.2.09 f = 50Hz U = 1730 V 0o Xd = 2.5 Ω Up = ε ⋅ U ⋅ e jβ I jXd U Up Stellen Sie I = f ( ε, β ) für die Wertebereiche 0 ≤ ε ≤ 2.5 und −90o ≤ β ≤ 90o dar! 5.6.2.10 R1 = 250Ω XC = 100Ω R2 = 200Ω XL = 200Ω R = p ⋅ R2 = 0...∞ 50Ω mZ = r = 4cm cm Zeichnen Sie die Ortskurve Y = f(R) ! jXL R2 R1 − jXC R Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.6.2.11 R1 = 8Ω X C = 5Ω XL = 10Ω R = pR2 = 0...∞ R2 = 10Ω 10mS mY = cm a) b) c) Aufgaben 05etu510 jXL R1 − jXC R Zeichnen Sie die Ortskurve Y = f(R) ! Bestimmen Sie den Widerstand R, bei dem Y reell wird! Bestimmen Sie den maximal einstellbaren Phasenwinkel! 5.6.2.12 R1 = 25Ω XC1 = 25Ω XL = 50Ω R2 = 100Ω XC = 0...∞ 25Ω mZ = cm a) b) 14 − jXC R1 mY = − jXC1 10mS cm R2 jXL Zeichnen Sie die Ortskurve Y = f(R) ! Bestimmen Sie den Wert XC, bei dem Y reell wird! 5.7 5.7.1 Spezielle Wechselstromschaltungen Passschaltungen 1. Ordnung 5.7.1.01 Gegeben ist nebenstehende Schaltung. C = 0.2 µF; R = 50 kΩ; a) Berechnen Sie die Übertragungsfunktion H! b) Geben Sie H für f = 50Hz in Prozent und den Pegel in dB an ! c) Berechnen Sie die Grenzfrequenz! Ue 1/ jωC R Ua Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 15 Aufgaben 05etu510 5.7.1.02 Gegeben ist der Hochpass von Aufgabe 5.7.101. a) Berechnen Sie den Widerstand R, wenn die Ausgangsspannung bei 50Hz: 1 %; 1.5 %; 2 % kleiner als Ue sein soll! b) Berechnen Sie die jeweiligen Verhältnisse von XC und R! 5.7.1.03 Gegeben ist ein R-L-Hochpass! a) Berechnen Sie die Grenzfrequenz ωG b) Bestimmen Sie diejenigen bezogenen Frequenzen ω / ωG , bei denen die Ausgangsspannung 0.99Ue bzw. 0.97Ue beträgt! 5.7.1.04 R1 = 600Ω L = 73.5mH GB = 0.5mS Uq = 100 V a) b) R1 Uq GB jXL Bestimmen Sie für das Hochpassnetzwerk die Grenzfrequenz und die maximale Wirkleistung am Verbraucher! Bestimmen Sie diese Werte, wenn GB so verändert wird, dass bei f → ∞ Anpassung herrscht! 5.7.1.05 j ωT 1 + j ωT ωT 1 GNä ( ω) = K ⋅ jωT Gegeben ist die Übertragungsfunktion: mit der Näherungsgeraden: G ( ω) = K ⋅ ωT 1 GNä ( ω) = K ωT 1 A / dB = 20 ⋅ lgK + 20 ⋅ lg ωT ωT 1 A / dB = 20 ⋅ lgK Geben Sie die Abweichungen der Betragskennlinie von den Näherungsgeraden an! Berechnen Sie die Abweichungen bei den Frequenzen ωg , 10ωg und 0.1ωg und sowie der Pegelfunktion: a) b) geben Sie die Abweichungen in dB an! 5.7.1.06 Gegeben ist nebenstehende Schaltung R = 1kΩ L = 100mH ue ( t ) = 1V ⋅ cos ωt R Ue jωL Ua Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 16 Aufgaben 05etu510 b) c) d) e) Ua und deren Betrag G! Ua Welche Eigenschaft hat die Schaltung (Hochpass, Tiefpass, Bandpass)? Bestimmen Sie die Grenzfrequenz und die Zeitkonstante! Zeichnen Sie das Bode-Diagramm! Berechnen Sie die Beträge der Übertragungsfunktion für ωg , 10ωg und 0.1ωg ! f) Berechnen Sie die Phasenverschiebung der komplexen Übertragungsfunktion für ωg , a) Berechnen Sie die komplexe Übertragungsfunktion G ( ω) = 10ωg und 0.1ωg ! g) Es sei ue ( t ) = 1V ⋅ cos ωg t . Geben Sie ua ( t ) = Ûa ⋅ cos ( ωg t + ϕ ) an! 5.7.1.07 Gegeben ist nebenstehender Tiefpass mit R = 5.1kΩ . Es oll die Grenzfrequenz fg = 1kHz eingestellt werden. Bestimmen Sie die Kapazität C des Kondensators! 5.7.1.08 Ein RC-Tiefpass wird am Ausgang mit dem Widerstand RB belastet. a) Bestimmen Sie den Frequenzgang G = Ua / Ue und stellen Sie ihn in der Normalform dar! Bestimmen Sie K, T und ωg ! b) R ue ua C R Ue 1 jωC RB Ua Die Werte der Bauelemente sind:R = RB = 5.1kΩ , C = 10nF . Die Amplitude der ˆ = 2V . Eingangsspannung ist U e Berechnen Sie die Grenzfrequenz fg und die Ausgangsspannung bei der Frequenz f = 0Hz ! 5.7.1.09 Gegeben ist nebenstehende Passschaltung: R = 1kΩ L = 10mH a) Berechnen Sie die Frequenzgänge G1 ( ω) , G2 ( ω) ! b) Charakterisieren Sie die beiden Frequenzgänge Ue (Tiefpass, Hochpass, Bandpass usw.)! ue = 1V ⋅ cos ωt , berechnen Sie Ua1, Ua2! Für welche Frequenz f1 wird Ua1 = Ua2 ? Berechnen Sie für diesen Fall die Ausgangsspannungen! Skizzieren Sie die Bode-Diagramme als Betrags- und Phasenkennlinie! c) d) R Ua1 jωL Ua2 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 17 Aufgaben 05etu510 5.7.1.10 Gegeben ist nebenstehendes Übertragungsglied zweiter Ordnung 1/ jωC C = 1nF L = 10mH Ue Ua R jωL Der Frequenzgang hat die Normalform 2 T02 ( jω) G ( ω) = K ⋅ 2 1 + 2dT0 jω + T02 ( jω) a) b) c) Berechnen Sie die Grenzfrequenzen der Betragskennlinie für d = 1 und d = 0.05 ! Berechnen Sie die Phasenverschiebung und den Betrag des Frequenzganges bei der Frequenz ω0 ! Skizzieren Sie mit K = 1 die Betragskennlinie des Bode-Diagramms für d = 1 und d = 0.05 ! 5.7.1.11 Gegeben ist nebenstehende Passschaltung mit: 1/ jωC R = 100kΩ C = 100nF . Ua Ue R a) Berechnen Sie den Frequenzgang U G ( ω) = a ! Zu welchem Typ gehört das Ue Übertragungsverhalten (Hochpass, Tiefpass usw.)? b) Skizzieren Sie das Bodediagramm des Frequenzganges, bestimmen Sie die Näherungsgeraden! c) Die Eingangsspannung hat folgende Funktion ue = 1V ⋅ cos ωt . Bestimmen Sie die ˆ = 1/ 2 V hat! Frequenz, bei der die Ausgangsspannung die Amplitude U a Berechnen Sie für diesen Fall die Periodendauer und die Nullphasenwinkel der Ausgangsspannung! 5.7.2 Passschaltungen höherer Ordnung 5.7.2.01 a) Berechnen Sie die Übertragungsfunktion H des nebenstehenden RC-Filters! R1 = R2 = R = 1kΩ; C1 = C2 = C = 3.185µF b) Bestimmen Sie diejenige Frequenz, bei der H maximal wird! c) Berechnen Sie den Maximalwert von H! R1 Ue 1/ jωC1 1/ jωC2 R2 Ua Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 18 Aufgaben 5.7.2.02 Gegeben ist nebenstehende Siebschaltung. R = 2kΩ; C = 32µF; a) Berechnen Sie die Übertragungsfunktion H! b) Auf welchen Wert wird eine 50-Hz-Spannung von Ue = 4.8 V herabgesetzt? 05etu510 R Ue 1/ jωC 1/ jωC Ua 5.7.2.03 Der Eingang eines Tuners wird durch einen Bandpass mit Parallelschwingkreis gebildet. Die Kapazität ist im Bereich C = 22...34pF einstellbar. Der Eingang ist mit einer Antenne beschaltet, deren Ersatzschaltung als lineare Spannungsquelle mit Ri = 1350Ω angesetzt wird. Bestimmen Sie die Bandmittenfrequenz und die Bandbreite in Abhängigkeit von der Kapazität C und stellen Sie beide Größen in einem Diagramm als Funktion von C dar! L = 100nH RB Ri R1 Uq 5.7.2.04 Ein Tiefpass zweiter Ordnung hat die Normalform: K mit K = 1 d = 5,05 G ( ω) = 1 + 2dT0 ( jω) + ( jωT02 ) a) b) c) jXL − jXC T0 = 10ms . Berechnen Sie T1 und T2 sowie die beiden Eckfrequenzen! Zeichnen Sie die Näherungsgeraden der Betragskennlinie und die Phasenkennlinie im Bodediagramm! Berechnen Sie Betrag und Phasenverschiebung bei den beiden Eckfrequenzen und bei der Frequenz, die eine Dekade oberhalb der höchsten Eckfrequenz und die eine Dekade unterhalb der niedrigsten Eckfrequenz liegt. 5.7.2.05 Gegeben ist ein Tiefpass 2. Ordnung mit den Eckfrequenzen ωg1 = 0.01s−1 und ωg2 = 0.1s−1 . Für kleine Frequenzen ist G = 0.1. a) b) RB Berechnen Sie K, ω0 und d! Skizzieren Sie die Betragskennlinie des Bode-Diagramms! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 19 Aufgaben 5.7.2.06 Gegeben ist eine Passschaltung nach nebenstehender Skizze. Die Dimensionierung ist: L = 10mH R = 20Ω a) Bestimmen Sie C für die Resonanzfrequenz f0 = 10kHz , die Resonanzüberhöhung und die Bandbreite! b) Bestimmen Sie den Widerstand R für den aperiodischen Grenzfall (Dämpfungsgrad d = 1 ! 05etu510 jωL R 1/ jωC UC U0 5.7.2.07 Gegeben ist nebenstehender Spannungsteiler: L = 10mH C = 10nF R1 = R2 = 1kΩ Übertragungsfunktion in Normalform: G ( ω) = U0 2dT0 jω U2 =K⋅ 2 U0 1 + 2dT0 jω + T02 ( jω) jωL 1/ jωC a) b) c) d) e) U1 R1 Berechnen Sie die Übertragungsfunktion G ( ω) = R2 U2 U2 und bestimmen Sie die U0 Werte T0 , ω0 , d, K ! Berechnen Sie den Betrag der Übertragungsfunktion für ω0 , 0.1ω0 und 10 ω0 ! Bestimmen Sie die Asymptoten von G für ω ω0 und ω ω0 Stellen Sie die in c) berechneten Asymptoten als Näherungsgeraden im BodeDiagramm dar und bestimmen Sie die Frequenz, bei der sich die Näherungsgeraden schneiden! Zeichnen Sie den tatsächlichen Verlauf der Übertragungsfunktion in das Bode-Diagramm ein indem Sie die Werte von G für ω0 , 0.1ω0 und 10 ω0 benutzen! Charakterisieren Sie das Übertragungsverhalten (Tiefpass, Hochpass, Bandpass, Bandsperre) mit Angabe der Ordnungszahl! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 20 Aufgaben 05etu510 5.7.2.08 Gegeben ist nebenstehendes Übertragungsglied zweiter Ordnung 1/ jωC C = 1nF L = 10mH Ue Der Frequenzgang hat die Normalform 2 T02 ( jω) G ( ω) = K ⋅ 2 1 + 2dT0 jω + T02 ( jω) a) b) c) jωL R Ua Ua der Schaltung! Ue Berechnen Sie K, d, ω0 als Funktion des Widerstandes R! Bestimmen Sie den Widerstand R für d = 1 ! C = 100nF L = 100mH d =1 jωL Ue Der Frequenzgang hat die Normalform 1 G ( ω) = K ⋅ 2 1 + 2dT0 jω + T02 ( jω) b) c) Ua Berechnen Sie den Frequenzgang G ( ω) = 5.7.2.09 Gegeben ist nebenstehendes Übertragungsglied zweiter Ordnung a) R 1/ jωC Ua und bestimmen Sie die Werte T0 , ω0 , K ! Ue Bestimmen Sie den Widerstand R für d = 1 ! Zeichnen Sie die Betragskennlinien des Bode-Diagramms für die Näherungen: ω ω0 und ω ω0 ! Bestimmen Sie die Frequenz des Schnittpunktes der Berechnen Sie G ( ω) = Näherungsgeraden (Grenzfrequenz ωg )! Skizzieren Sie den tatsächlichen Verlauf G ( ω) im Bereich der Grenzfrequenz! 5.7.2.10 Eine Freileitung von 100 km Länge besitzt die Widerstandswerte 2R = 16Ω; 2XL = 24Ω; 2XC = 4000Ω. In untenstehender Skizze ist die Ersatzschaltung der Leitung gegeben. a) Berechnen Sie H für die leerlaufende Leitung! b) Die Leitung wird mit ZL = RL + j XLL belastet (RL = 300Ω; XLL = 200Ω). Berechnen Sie für diesen Belastungsfall H! Ue R 2 j XL 2 R − jXC j XL − jXC R 2 j XL 2 Ua Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 21 Aufgaben 05etu510 5.7.2.11 Berechnen Sie den Siebfaktor S = 1/H für die angegebene Siebkette bei f = 50 Hz! 50kΩ 0.8µF 50kΩ 0.8µF 0.8µF 5.7.2.12 a) Berechnen Sie die Übertragungsfunktion H für die angegebene Phasenkette! b) Bestimmen Sie den Wert R ⋅ ω ⋅ C , bei dem die Funktion reell wird! c) Berechnen Sie H für diesen Fall! C C R C R R 5.7.2.13 a) Berechnen Sie die Übertragungsfunktion H für die angegebene Phasenkette! b) Bestimmen Sie den Wert R ⋅ ω ⋅ C , bei dem die Funktion reell wird! c) Berechnen Sie H für diesen Fall! R R R C C C Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.7.3 22 Aufgaben 05etu510 Schwingkreise 5.7.3.01 Gegeben ist ein Reihenresonanzkreis: L = 9.6mH; RL = 11Ω; C = 0.33µF Berechnen Sie: a) Resonanzfrequenz fr b) Verlustfaktor tan δ bei fr c) Resonanzüberhöhung (Resonanzgüte) d) 45°- Frequenzen und Bandbreite bf e) Betrag des Scheinwiderstandes Z bei den Frequenzen: fr; 21 fr ; 2fr; f+45°; f-45° f) Betrag des Stromes I bei den unter e) angegebenen Frequenzen und einer konstanten Netzspannung U = 10 V. g) Betrag der Teilspannungen UL und UC bei den unter e) angegebenen Frequenzen bei einer konstanten Gesamtspannung U = 10 V. h) Stellen Sie die unter f) und g) berechneten Funktionen grafisch dar. 5.7.3.02 Der in Aufgabe 5.7.2.01 angegebene Reihenschwingkreis wird durch Parallelschalten eines Kondensators C1 = 0.33 µF zum ursprünglichen Kondensator verändert. Wie ändern sich die Ergebnisse der Aufgabe 5.7.1.01 a) bis d)? 5.7.3.03 Der Schwingkreis in Aufgabe 5.7.1.01 soll eine Bandbreite bf = 300 Hz erhalten. Wie ist die Schaltung zu verändern? Wie ändern sich die Ergebnisse der Aufgabe 5.7.1.01 a) bis d)? 5.7.3.04 Die Spannung über der Induktivität des Reihenschwingkreises der Aufgabe 5.7.1.01 kann nicht direkt gemessen werden, da R und L Parameter einer technischen Spule sind. Mit Uspule wird die Spannung über der Reihenschaltung von R und L erfasst. Berechnen Sie den Fehler im Frequenzbereich fr - 100 Hz < fr < fr + 100 Hz, wenn man bei der Messung den ohmschen Spulenwiderstand vernachlässigt (USpule = UL). 5.7.3.05 Berechnen Sie das Verhältnis der Beträge der Scheinwiderstände bei Resonanzfrequenz und den 45°-Frequenzen allgemein und mit den Werten der Aufgabe 5.7.1.01! 5.7.3.06 Die Reihen-Ersatzschaltung einer technische Spule besteht aus der Reihenschaltung eines ohmschen Widerstandes RL und einer Induktivität L. Berechnen Sie für eine Spule mit den Werten XL = 5.86Ω und RL = 11Ω die entsprechenden Werte von RP und XP des äquivalenten Parallelkreises. RL jXL RP jXP Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 23 Aufgaben 05etu510 5.7.3.07 Zu der Spule (L = 9.6mH; RL = 11Ω) wird ein Kondensator (C = 0.33µF) und ein ohmscher Widerstand R1 parallel geschaltet und damit ein Parallelresonanzkreis aufgebaut. Berechnen Sie für eine Güte ρ = 10 den notwendigen Widerstand R1,wobei a) von einer idealen Spule (RL = 0) ausgegangen wird b) der ohmsche Widerstand der Spule RL berücksichtigt wird. Wie groß kann die Güte ρ maximal werden, wenn kein zusätzlicher Widerstand parallel geschaltet wird? Der Kondensator wird als verlustfrei angenommen. 5.7.3.08 Dimensionieren Sie ein Bandfilter mit Reihenschwingkreis, das mit einer Spannungsquelle mit zeitlich sinusförmigem Spannungsverlauf Uq = 6V; Ri = 10Ω Uq betrieben wird. Am Verbraucher soll die maximale Leistung PBmax = 500mW verfügbar sein. Die Grenzfrequenzen sind: fGu = 9950Hz; fGo = 10050Hz. Bestimmen Sie die Werte von L, C und RB sowie den Maximalwert der Spannung an L und C! UL R1 jXL UC − jXC ⇒ PB RB 5.7.3.09 Gegeben ist nebenstehendes Schwingkreis mit C = 10nF L = 10mH ρ = 20 1 ω0 = Resonanzfrequenz LC 1 L Z0 = ω0L = = Kennwiderstand ω0C C R ρ= Resonanzüberhöhung Z0 1/ jωC jωL R b) c) Berechnen Sie Resonanzfrequenz ω0 und Kennwiderstand Z0! Bestimmen Sie den für die Resonanzüberhöhung ρ = 20 notwendigen Widerstand R! Berechnen Sie den Widerstandsoperator Z des Schwingkreises! Bestimmen Sie Z ( ω) und ϕZ ( ω) ! d) Bestimmen Sie die Frequenzen für Phasenresonanz f0 und Amplitudenresonanz fA ! e) f) Berechnen Sie die Frequenzen für 3dB-Bandbreite ( 45o -Frequenzen)! Skizzieren Sie die Betragskennlinie Z ( lg ω / ω0 ) in linearer Darstellung! g) Die Spannung über dem Schwingkreis hat den Zeitverlauf u = 2 ⋅ 10V ⋅ cos ωt . Berechnen Sie die Zeiger der Ströme durch L, C und R bei Phasenresonanz! a) Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.7.4 24 Aufgaben 05etu510 Brückenschaltungen 5.7.4.01 Uq = 10V; UL f = 50Hz R1 = 50Ω XL = 35Ω R2 = 40Ω R3 = 30Ω R1 jXL R3 R2 UX XC = 210Ω a) b) Zeichnen Sie für nebenstehende Brückenschaltung das maßstäbliche Zeigerbild der Spannungen mU = 1V/cm Auf welche Werte müssen die Widerstände R4 und R5 eingestellt werden, damit die Spannungen UL und UX phasen- und betragsgleich werden ( UL = UX )? 5.7.4.02 Uq = 100V; f = 50Hz R1 = 40Ω XL = 20Ω R2 = 20Ω XC1 = XC2 = 20Ω a) b) a) b) Uq R1 f = 50Hz Auf welchen Wert muss der Widerstand R3 eingestellt werden, damit UX minimal wird? Im oberen Brückenzweig werden folgende Spannungen gemessen: UR1 = 10V; UC1 = 80V; UR2 = UL = 40V Bestimmen Sie den Betrag der Quellenspannung der Spannungsquelle! − jXC1 R2 UAB R3 Auf welchen Wert muss R3 eingestellt werden, damit die Spannungen Uq und UAB 90o Phasenverschiebung haben? Zeichnen Sie das maßstäbliche Zeigerbild aller Spannungen mU = 10V/cm! 5.7.4.03 XC2 = 80Ω R5 R4 − jXC − jXC2 jXL Uq R1 − jXC1 UX jXL R2 R3 − jXC2 Uq Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.7.4.04 Uq = 10V 0o 25 Aufgaben 05etu510 f = 50Hz R1 = R2 = XC1 = XL = 50Ω R 4 = 29Ω Die Spannung UEF soll gegenüber der Quellenspannung Uq um 90o vorauseilen a) Entwickeln Sie für die Brückenschaltung ein maßstäbliches Zeigerbild der Spannungen mit mu = 1V/cm! Beginnen Sie mit UEF = 7.9V 90o b) Ermitteln Sie aus dem Zeigerbild die Spannungen UAF und UFB und überprüfen Sie das Ergebnis durch Berechnung! c) Bestimmen Sie die Werte R3, XC2 und C2! 5.7.4.05 Gegeben ist nebenstehende Brückenschaltung (Wien-Robinson-Brücke), bei der die beiden gleichen Kondensatoren gemeinsam verstellt werden können. U a) Bestimmen Sie das Verhältnis X ! Uq b) Für welches Verhältnis R3/R4 und welche Frequenz ω0 ist die Brücke abgeglichen? c) Geben Sie für das in b) ermittelte Verhältnis R3/R4 die komplexe Funktion ω UX an! = f(p) mit p = ω0 Uq E R1 − jXC1 UEF R2 jXL A B F R3 R4 − jXC2 Uq − jXC R − jXC R UX R4 R3 Uq