Ferienkurs Experimentalphysik 2

Ferienkurs Experimentalphysik 2
Sommersemester 2015
Gabriele Semino, Alexander Wolf, Thomas Maier
Vorlesung 2
Elektrischer Strom und Magnetostatik
Nach dem Skript "Konzepte der Experimentalphysik 2: Elektromagnetismus"
von Abel Perera, Andrea Meraner, Gabriele Semino und Adonia Siegmann
Inhaltsverzeichnis
2 Elektrischer Strom
1
2.1
Strom als Ladungstransport und Kontinuitätsgleichung . . . . . . . . . . .
1
2.2
Kirchhoff’sche Regeln für Netzwerke . . . . . . . . . . . . . . . . . . . . . .
2
2.3
Elektrischer Widerstand . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2.3.1
Ohm’sches Gesetz . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
2.3.2
Elektrische Leistung und Joule’sche Wärme . . . . . . . . . . . . .
4
2.3.3
Widerstandsschaltungen . . . . . . . . . . . . . . . . . . . . . . . .
4
3 Magnetostatik
3.1
3.2
3.3
3.4
6
Feldgleichungen und Vektorpotential . . . . . . . . . . . . . . . . . . . . .
6
3.1.1
Magnetischer Kraftfluss und erste magnetische Feldgleichung . . . .
6
3.1.2
Zweite magnetische Feldgleichung . . . . . . . . . . . . . . . . . . .
6
3.1.3
Das magnetische Vektorpotential . . . . . . . . . . . . . . . . . . .
7
Magnetfelder spezieller Anordnungen . . . . . . . . . . . . . . . . . . . . .
7
3.2.1
Das Ampere’sche Durchflutungsgesetz
. . . . . . . . . . . . . . . .
7
3.2.2
Das Biot-Savart-Gesetz . . . . . . . . . . . . . . . . . . . . . . . . .
8
Kräfte auf bewegte Ladungen im Magnetfeld . . . . . . . . . . . . . . . . . 10
3.3.1
Kräfte auf stromdurchflossene Leiter im Magnetfeld . . . . . . . . . 10
3.3.2
Hall-Effekt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Magnetische Dipole . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.4.1
Magnetisches Dipolmoment . . . . . . . . . . . . . . . . . . . . . . 11
3.4.2
Magnetischer Dipol im äußeren Magnetfeld . . . . . . . . . . . . . . 12
3.4.3
Magnetisches Dipolmoment von Atomen . . . . . . . . . . . . . . . 13
3.5
Magnetisierung und Suszeptiblität . . . . . . . . . . . . . . . . . . . . . . . 13
3.6
Arten der Magnetisierung . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Abbildungsquellen
16
I
2
2.1
Elektrischer Strom
Strom als Ladungstransport und Kontinuitätsgleichung
Während wir uns bisher in der Elektrostatik mit stationären Ladungen befasst haben,
betrachten wir jetzt den Fall bewegter Ladungen. Als erste wichtige Definition führen wir
den elektrischen Strom ein; dieser gibt an, wie viele Ladungen pro Zeiteinheit durch eine
bestimmte Fläche A fließen.
I :=
dQ
dt
[I] = 1
C
= 1 A = 1 Ampere
s
(2.1.1)
Im Moment betrachten wir den Fall stationärer Ströme, also solche, die in der Zeit konstant sind (dI/ dt = 0). Da laut Definition der Strom durch eine bestimmte Fläche A
fließt, können wir analog zur Ladungsdichte in der Elektrostatik die Stromdichte ~j(~r)
definieren, als Strom pro Fläche, oder anders ausgedrückt wie folgt:
¨
~
~j(~r) · dA
(2.1.2)
I=
A
Der Anschaulichkeit halber betrachten wir auch folgende, oft in einfacheren Fällen verwendete, Formel. Man stelle sich z.B. einen homogenen stromdurchflossenen Leiter mit
dem Querschnitt A vor.
I
(2.1.3)
j=
A
Die Ladungsträger können beispielsweise Ionen oder „freie“ Elektronen sein. Sei dafür n
die Dichte der Ladungsträger im Leiter, q deren Ladung und ~v deren Geschwindigkeit.
Aus einfacher Überlegung folgt für die Stromdichte folgender Ausdruck.
~j = nq~v
(2.1.4)
Dies beschreibt tatsächlich die Bewegung von Ladungen durch eine Fläche; durch Integration über diese erhält man den analogen Ausdruck für den elektrischen Strom. Aus
Konvention wird als technische Stromrichtung die Bewegungsrichtung von positiven Ladungsträger definiert.
Kontinuitätsgleichung
Betrachtet man eine geschlossene Fläche, so folgt direkt aus der Ladungserhaltung folgende Gleichung.
˚
‹
d
dQ
~
~
=−
ρ dV
(2.1.5)
I=
j(~r) · A = −
dt
dt
V
A=∂V
Dies ist die sogenannte Kontinuitätsgleichung; der Fluss des Stromes durch eine geschlossene Fläche muss gleich der zeitlichen Änderung der eingeschlossenen Ladung sein. Vergleich
mit dem Gauß’schen Gesetz liefert die differentielle Form dieser Gleichung.
div ~j(~r) = −
1
∂ρ(~r, t)
∂t
(2.1.6)
2.2
Kirchhoff’sche Regeln für Netzwerke
Die Kirchhoff’schen Regeln beschreiben die allgemeinen Strom- und Spannungseigenschaften eines Netzwerkes (bzw. einer Schaltung).
• 1. Kirchhoff’sche Regel (Knotenregel)
Aus der Kontinuitätsgleichung (Ladungserhaltung) ergibt sich, dass die Summe der in
einen Knoten einlaufenden Ströme gleich der Summe der auslaufenden Ströme ist.
I1 + I2 = I3
Und allgemein
X
Iein =
X
Ik = 0
X
Iaus
(2.2.1)
k
Abbildung 2.1: Zur Knotenregel(1)
Einlaufende Ströme haben somit umgekehrtes Vorzeichen wie auslaufende.
• 2. Kirchhoff’sche Regel (Maschenregel)
Aufgrund der Energieerhaltung gilt, dass in jedem geschlossenen Stromkreis (Masche)
die Summe aller Verbraucherspannungen (z.B Kondensatoren, Widerstände) gleich der
Generatorspannungen ist.
U1 + U2 + U3 = 0
Und allgemein
X
Uk = 0
(2.2.2)
Masche
Abbildung 2.2: Zur Maschenregel(1)
2.3
2.3.1
Elektrischer Widerstand
Ohm’sches Gesetz
Ladungen bewegen sich in Leitern im Allgemeinen einerseits aufgrund der thermischen
Energie des Materials, andererseits aufgrund elektrischer Felder. Man betrachte zuerst
den Fall eines Leiters, der sich nicht in einem elektrischen Feld befindet. Die Ladungsträger bewegen sich also nur aufgrund ihrer thermischen bzw. kinetischen Energie. Diese
Bewegungen erfolgen zufällig in alle möglichen Richtungen und unterscheiden sich betragsmäßig bei allen Teilchen. Darüber hinaus stoßen die Teilchen ständig zusammen,
2
was zum Wechsel von Richtung und Betrag der Geschwindigkeiten der Teilchen führt.
Wegen dieser beschriebenen Verteilung der Richtungen muss die mittlere Geschwindigkeit gleich null sein (h~v i = 0). Setzt man diesen Wert in die oben erhaltene Gleichung
2.1.4 ein, so erhält man für die Stromdichte in diesem Fall folgenden Wert.
~j = nqh~v i = 0
Nur durch thermische Energie kann also kein Strom produziert werden. Zur weiteren
Rechnung ist die mittlere Zeit zwischen zwei Stößen wichtig.
τs =
Λ
v̄
wobei Λ die mittlere freie Weglänge und v̄ die mittlere Geschwindigkeit der Ladungsträger
ist. Letztere ist nicht null, weil man dabei nur über die Beträge der Geschwindigkeiten
mittelt, also unabhängig von der Richtung der Bewegung. Wird jetzt ein elektrisches Feld
eingeschaltet, so erhalten die Teilchen in der Zeit zwischen zwei Stößen die Zusatzgeschwindigkeit
qE
τs
∆v = aτs =
m
wobei q die Ladung des Ladungsträgers, m dessen Masse und E die angelegte Feldstärke
ist. Mittelt man diese Geschwindigkeit über alle Teilchen, so erhält man die sogenannte
Driftgeschwindigkeit.
h∆~v i = ~vD
Die Ladungsträger bewegen sich in diesem Fall durchschnittlich mit dieser Geschwindigkeit mit bzw. gegen das elektrische Feld, abhängig von deren Ladung. Setzt man diese
Geschwindigkeit in Gleichung 2.1.4 ein, so erhält man den folgenden Ausdruck für die
Stromdichte.
Ohm’sches Gesetz
2
~ = σE
~
~j = nq~vD = nq τs E
m
(2.3.1)
Die definierte Größe σ wird elektrische Leitfähigkeit genannt. Analog dazu kann der spezifische Widerstand definiert werden als das Inverse der Leitfähigkeit (ρs = 1/σ).
Für homogene Leiter mit Querschnitt A und Länge L ergibt sich aus
ˆ
¨
~ · dL
~ = EL
~ = jA,
~j · dA
U=
E
und
I=
(2.3.2)
L
A
Ohm’sches Gesetz in integraler Form
I=
σA
U
U=
L
R
(2.3.3)
Das Inverse des Proportionalitätsfaktors zwischen Strom und Spannung ist der sogenannte
elektrische Widerstand.
3
Elektrischer Widerstand
R=
2.3.2
1L
L
= ρs
σA
A
[R] = 1
V
= 1 Ω = 1 Ohm
A
(2.3.4)
Elektrische Leistung und Joule’sche Wärme
Legt man eine Potentialdifferenz zwischen zwei Enden eines Leiters (mit einem gewissen Widerstand) an, fließt durch diesen ein Strom. In einem Widerstand fällt also die
Spannung ab, d.h. Ladungstransport innerhalb eines Widerstandes erfordert eine gewisse
Energie. Diese kann mit den Mitteln der Elektrostatik leicht bestimmt werden.
Für die elektrische Arbeit definieren wir nun zweckmäßig
W = q(φ1 − φ2 ) = qU
(2.3.5)
Ableiten dieser Gleichung nach der Zeit liefert einen Ausdruck für die elektrische Leistung.
P =
dW
dq
=U
= UI
dt
dt
[P ] = 1W = 1 Watt
(2.3.6)
Mithilfe von Gleichung 2.3.3 kann man den obigen Ausdruck umschreiben.
Leistung eines Widerstandes
P = U I = I 2R =
U2
R
Integration von Gleichung 2.3.6 liefert die integrale Form von Gleichung 2.3.5.
ˆ t2
ˆ t2
W =
P dt =
U I dt
t1
(2.3.7)
(2.3.8)
t1
Die in einem Widerstand verbrauchte Energie wird durch Reibungskraft in Wärme umgewandelt.
2.3.3
Widerstandsschaltungen
Analog zu den Kondensatorenschaltungen kann man für ein Netzwerk von Widerständen
einen äquivalenten (gesamten) Widerstand berechnen. Ein solcher Widerstand bewirkt
alleine den selben Spannungsabfall wie das gesamte Widerstandsnetz. Mithilfe der Kirchhoff’schen Regeln können wir folgende Gleichungen herleiten.
4
• Parallelschaltung
U = U1 = U2 = Ui
I = I1 + I2 + ...
1
1
+
+ ...
=U
R1 R2
⇒
Abbildung 2.3: Schaltbild einer Parallelschaltung von Widerständen(1)
X 1
1
=
Rges
i Ri
(2.3.9)
(2.3.10)
• Serienschaltung
U = R1 I + R2 I + ...
= (R1 + R2 + ...)I
(2.3.11)
I = I1 = I2 = Ii
Abbildung 2.4: Schaltbild einer Serienschaltung von Widerständen(1)
⇒ Rges =
X
i
5
Ri
(2.3.12)
3
Magnetostatik
Magnetische Felder werden von Permanentmagneten und von bewegten Ladungen erzeugt.
Die Stärke von magnetischen Feldern wird durch die magnetische Erregung (magnetische
~ und die magnetische Flussdichte (auch Magnetfeld genannt) B
~ beschrieben.
Feldstärke) H
~ und der elektrischen
Diese zwei Größen sind, analog zur dielektrischen Verschiebung D
~ im Vakuum durch folgende Relation verknüpft.
Feldstärke E,
~ = µ0 H
~
B
[B] = 1 Tesla = 1T = 1
Vs
m2
(3.0.1)
wobei µ0 = 4π · 10−7 AN2 die sogenannte magnetische Feldkonstante ist.
3.1
3.1.1
Feldgleichungen und Vektorpotential
Magnetischer Kraftfluss und erste magnetische Feldgleichung
Analog zum elektrischen Fluss durch eine Oberfläche können wir den magnetischen Kraftfluss wie folgt definieren.
¨
~ · dA
~
Φmag =
B
(3.1.1)
A
Die Feldlinien magnetischer Felder sind, im Gegensatz zu denen von elektrischen Feldern,
immer geschlossen. Deswegen verschwindet der Kraftfluss immer im Fall von geschlossenen
Oberflächen.
‹
~ · dA
~=0
B
(3.1.2)
Φmag =
∂V
Aus dem Vergleich dieser Gleichung mit dem Gauß’schen Gesetz erhält man die differentielle Form der 1. Feldgleichung für magnetische Felder.
~ =0
div B
(3.1.3)
Aus Gleichung 3.1.2 kann man auch schließen, dass es keine magnetischen Monopole gibt
bzw. „Quellen“ wie die Ladungen beim elektrischen Feld.
3.1.2
Zweite magnetische Feldgleichung
Analog zum Fall elektrischer Felder betrachten wir hier auch eine zweite Gleichung zur
Beschreibung von magnetischen Feldern. Es stellt sich in diesem Fall experimentell heraus,
dass für die Rotation von magnetischen Feldern folgende Gleichung gilt.
~ = µ0~j
rot B
Die Kernaussage: Stromdichten erzeugen rotierende magnetische Felder.
6
(3.1.4)
3.1.3
Das magnetische Vektorpotential
Als weitere Analogie zu den elektrischen Feldern wollen wir jetzt ein magnetisches Potential definieren. Wegen der obigen Feldgleichung ist eine analoge Definition jedoch nicht
möglich. Eine solche Definition
~ = − grad φmag
B
(3.1.5)
führt zum folgenden Widerspruch mit Gleichung 3.1.4.
~ = rot grad φmag = 0
rot B
Dies ist natürlich eine Folge der Tatsache, dass magnetische Felder nicht konservativ
sind. Eine alternative Definition ist jedoch möglich: wir machen in diesem Fall folgende
Annahme.
~ = rot A
~
B
(3.1.6)
Da ein solches Vektorpotential bis auf den Gradienten einer skalaren Ortsfunktion definiert
~ gibt),
ist (wodurch es unendlich viele Möglichkeiten für A
~0 = A
~ + grad f (~r)
A
~ 0 = rot A
~ + rot grad f (~r) = rot A
~
rot A
⇒
(3.1.7)
wird die sogenannte Coulomb-Eichung eingeführt:
~=0
div A
(3.1.8)
~ Setzt man die obige Definition des Vektorpotentials
Dies sichert die Eindeutigkeit von A.
in die Feldgleichungen ein, so erhält man folgende Zusammenhänge:
~ = div rot A
~=0
div B
~ = rot rot A
~ = grad div A
~ − ∆A
~ = −∆A
~ = µ0~j
rot B
3.2
3.2.1
(3.1.9)
Magnetfelder spezieller Anordnungen
Das Ampere’sche Durchflutungsgesetz
Eine wichtige Anwendung von Gleichung 3.1.4 ist das sogenannte Ampere’sche Gesetz.
Mithilfe dieser Gleichung und dem aus der Vektoranalysis bekannten Stokes’schen Satz
˛
¨
~
~v · d~r =
rot ~v · dA
(3.2.1)
∂A
A
können wir folgendes, für die Anwendung sehr wichtiges, Gesetz herleiten:
Ampere’sches Durchflutungsgesetz
˛
¨
¨
~
~
~
~ = µ0 I
~j · dA
B · d~r =
rot B · dA = µ0
∂A
A
(3.2.2)
A
Die Anwendung dieses Gesetzes ist analog zum Gauß’schen Gesetz in der Elektrostatik
und soll am folgenden Beispiel verdeutlicht werden.
7
Beispiel: Magnetisches Feld eines geraden stromdurchflossenen Drahtes
Als einfaches Beispiel zur Anwendung dieses Gesetzes nehmen wir einen homogen stromdurchflossenen Draht. Zur Auswertung der zwei Integrale nehmen wir eine geschlossene
kreisförmige Kurve mit Radius r, dessen Mittelpunkt der Draht ist und die auf einer Ebene senkrecht zu diesem liegt. Aus Symmetriegründen muss das magnetische Feld entlang
einer solchen Kurve konstant sein und die Feldlinien sind parallel zu der Integrationskur~
ve, also gilt B(r)
= B(r)~eϕ (siehe Schraubenzieher bzw. Rechte-Hand-Regel). Die linke
Seite des Ampere’schen Gesetzes kann deswegen wie folgt berechnet werden.
˛
˛
~
B · d~r = B ·
~eϕ · d~r = 2πrB(r)
(3.2.3)
∂A
∂A
Gleichsetzen der obigen Gleichungen liefert uns einen Ausdruck für die magnetische Flussdichte.
µ0 I
~
~eϕ
(3.2.4)
B(r)
=
2πr
Abbildung 3.1: Anwendung des Ampere’schen Gesetzes auf den stromdurchflossenen
Leiter(17)
3.2.2
Das Biot-Savart-Gesetz
Ein weiteres wichtiges Gesetz für die Berechnung der durch stromdurchflossene Leiter erzeugten magnetischen Felder lässt sich aus der folgenden, schon oben erwähnten Gleichung
herleiten.
~ = −µ0~j
∆A
(3.2.5)
Obige Differentialgleichung hat folgende allgemeine Lösung.
~ r ) = µ0
A(~
4π
˚
V
~j(~r 0 )
dV 0
|~r − ~r 0 |
(3.2.6)
Für V soll in diesem Fall das ganze vom Strom durchflossene Volumen betrachtet werden.
Aus dieser Gleichung lässt sich das Biot-Savart-Gesetz herleiten.
~ r ) = rot A
~ = rot µ0
B(~
4π
Ausgerechnet ergibt dies:
8
˚
V
~j(~r 0 )
dV 0
0
|~r − ~r |
!
(3.2.7)
Biot-Savart-Gesetz
~ r ) = − µ0 I
B(~
4π
˛
L
~r − ~r 0
× d~r 0
|~r − ~r 0 |3
(3.2.8)
Dabei ist ~r 0 der Vektor, der die Form des Leiter beschreibt.
Beispiel: Magnetisches Feld eines geraden stromdurchflossenen Drahtes
Wir wollen wieder das Beispiel des stromdurchflossenen unendlichen Leiter nutzen, machen die Berechnung aber mit dem Biot-Savart-Gesetz. Als Erstes definieren wir die Form
des unendlich langen Leiters mit dem Vektor ~r 0 und berechnen das differentielle Bogenelement (der Leiter ist o.B.d.A. auf der z−Achse).
~r 0 = (0, 0, z 0 )
d~r 0 = dz 0~ez
Da ~r = (x, y, z) ein allgemeiner Vektor ist (er beschreibt den Punkt im Raum, an welchem
das magnetische Feld gemessen wird), gelten folgende Zusammenhänge:
2
|~r − ~r 0 | = x2 + y 2 + (z − z 0 )2
(~r − ~r 0 ) × d~r 0 = − dz 0 (−y, x, 0)
Es folgt also für das magnetische Feld.
~ r ) = µ0 I
B(~
4π
ˆ

∞
−∞
(x2
+
y2
1
+ (z − z 0 )2 )3/2

−y

 0
 x  dz
0
−y ˆ
1
µ0 I   ∞
dz 0
=
 x 
2
4π
(r + (z − z 0 )2 )3/2
−∞
0




−y
µ0 I   µ0 I
~eϕ
=
 x =
2πr
2πr
0
(3.2.9)
Die Lösung des Integrals ist nicht elementar und erfolgt mittels folgender Substitution:
z − z 0 = r tan ψ
Hinweis: Ampere oder Biot-Savart?
Als grobe Faustregel gilt: Ist der Leiter unendlich lang, so wird im Normalfall das Ampere’sche Gesetz benutzt; fließt der Strom in einer Leiterschleife, so nutzt man das BiotSavart’sche Gesetz. Beide Gesetze sind aber allgemein immer gültig; die richtige Wahl
vereinfacht jedoch die Problemstellung sehr.
9
3.3
Kräfte auf bewegte Ladungen im Magnetfeld
~ mit der Geschwindigkeit ~v , so
Bewegt sich eine Ladung q innerhalb eines Magnetfeldes B
spürt sie die sogenannte
Lorentzkraft
~
F~ = q(~v × B)
(3.3.1)
~ so ergibt sich die folgende Gesamtkraft auf die
Wirkt zusätzlich ein elektrisches Feld E,
Ladung.
~ + E)
~
F~ = q(~v × B
(3.3.2)
3.3.1
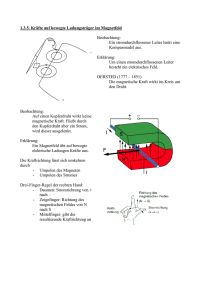
Kräfte auf stromdurchflossene Leiter im Magnetfeld
Abbildung 3.2: Zur Berechnung der Kraft auf ein infinitesimal kurzes Drahtstück(1)
Man betrachte ein infinitesimal kurzes Drahtstück der Länge dL. Die bewegte Ladung in
diesem Stück ist durch folgende Gleichung gegeben.
dQ = nqA dL
(3.3.3)
So ist die Kraft auf ein solches Stück gegeben durch
~ dQ = nqA(~v × B)
~ dL
dF~ = (~v × B)
(3.3.4)
Mithilfe von Gleichung 2.1.4 lässt sich obige Gleichung wie folgt schreiben.
~ dL = (~j × B)
~ dV
dF~ = (~j × B)A
(3.3.5)
Im Fall von geraden Drähten in einem homogenen Magnetfeld kann man diese Gleichung
wie folgt vereinfachen.
Lorentzkraft auf einen geraden stromdurchflossenen Draht
~ × B)
~
dF~ = I(dL
(3.3.6)
Darüber hinaus lässt sich im Fall von parallelen stromdurchflossenen Drähten im Abstand
R der folgende Ausdruck für die Kraft pro Längeneinheit schreiben.
F2
µ0 I1 I2
= I2 B1 =
(3.3.7)
L
2π R
10
3.3.2
Hall-Effekt
Abbildung 3.3: Hall-Effekt(4)
Befindet sich ein Leiter in einem Magnetfeld und wird er von Strom durchflossen, so
erfahren die Ladungsträger eine Ablenkung durch die Lorentzkraft. Aus diesem Grund
bildet sich zwischen den Seitenflächen eine Spannung. Die Ablenkung der Ladungsträger
erfolgt, bis die aufgebaute Spannung eine Kraft erzeugt, die so stark wie die Lorentzkraft
ist. Es gilt also
~ H = q~v × B
~
qE
(3.3.8)
~ H = UH~b ein, so erhält man den folgenden Ausdruck für
Setzt man Gleichung 2.1.4 und E
die sogenannte Hall-Spannung.
UH = −
~ · ~b
(~j × B)
nq
(3.3.9)
Obige Formel lässt sich mithilfe von I = Aj = bdj und durch Ausrechnen des Vektorprodukts wie folgt vereinfachen.
IB
UH =
= RH I
(3.3.10)
nqd
Der somit definierte Hall-Widerstand RH lässt sich messen und daraus lässt sich dann die
Ladungsträgerdichte für verschiedene Materialien bestimmen.
3.4
3.4.1
Magnetische Dipole
Magnetisches Dipolmoment
Analog zum elektrischen Dipolmoment kann das magnetische Dipolmoment p~m definiert
werden. Das Feldlinienbild eines solchen Dipols gleicht dem eines kurzen Stabmagneten.
Aus dem Biot-Savart-Gesetz folgt, dass ein stromdurchflossener Draht ein magnetisches
Feld erzeugt; es stellt sich heraus, dass das Magnetfeld einer ebenen, geschlossenen Stromschleife dem eines kurzen permanenten Dipolmagneten entspricht.
11
Abbildung 3.5: Stromschleife(6)
Abbildung 3.4: Magnetstab(6)
Es kann somit das magnetische Dipolmoment einer stromdurchflossenen Schleife
wie folgt definiert werden:
~
p~m = I · A
(3.4.1)
~ der Vektor ist, dessen Betrag die Fläche innerhalb der Leiterschleife ist und dessen
wobei A
Richtung orthogonal zur Fläche steht. Liegt die Schleife in der x-y-Ebene, so ergibt sich
für das magnetische Feld in Fernfeldnäherung.
~ = µ0 p~m
B
2π r3
3.4.2
(3.4.2)
Magnetischer Dipol im äußeren Magnetfeld
Befindet sich ein magnetischer Dipol in einem äußeren magnetischen Feld, so wirkt auf
diesen ein Drehmoment
~ = p~m × B
~
D
(3.4.3)
Die potentielle Energie des Dipols lässt sich analog zum elektrostatischen Fall herleiten
und es gilt:
~
Epot = −~pm · B
(3.4.4)
Analog zum elektrostatischen Fall ist die totale resultierende Kraft auf einen magnetischen
Dipol in einem homogenen Feld gleich Null, während sich im inhomogenen Feld folgende
Kraft ergibt
~ pot = ∇(~
~ pm · B)
~
F~ = −∇E
(3.4.5)
Man vergleiche dazu Gleichung 1.2.8.
Nach obiger Überlegung sollten diese Gleichungen auch für stromdurchflossene Schleifen in Magnetfelder gelten. Dies soll nun für Gleichung 3.4.3 bestätigt werden.
Man betrachte hierzu eine rechteckige Leiterschleife mit den Kantenlänge l1,3 = a, l2,4 = b,
welche drehbar um die Achse C gelagert ist.
12
Abbildung 3.6: Stromschleife in äußeren Magnetfeld(4)
Wird nun wie nach obiger Zeichung ein magnetisches Feld angelegt, so wirkt auf die
einzelnen Seiten die Lorentz-Kraft
~
F~L,i = li I(~ei × B)
Der Vektor ~ei zeigt entlang der jeweiligen Seite und in Richtung des fließenden Stroms I.
Es wirken somit Kräfte senkrecht zu den jeweiligen Seiten und dem Magnetfeld. Kräfte
auf die Seiten 2 und 4 löschen sich gegenseitig aus (bzw. werden durch die Aufhängung
aufgehoben), während die Kräfte auf die Seiten 1 und 3 mithilfe der Lorentzkraft und
dem Hebelarm ~r1,3 = 2b ~e4,2 das folgende Drehmoment erzeugen:
~ =I ·A
~×B
~
~ = ~r4 × F~L,1 + ~r2 × F~L,3 = 2 · b · aI(~eb × ~ea ) × B
D
|{z} | {z }
2
−~
r4
(3.4.6)
~L,1
−F
was mit p~m = I · A zur Gleichung 3.4.3 führt.
3.4.3
Magnetisches Dipolmoment von Atomen
Das Prinzip des Kreisstroms (kreisförmige Schleife) kann man auf die Elektronen eines
Atomes anwenden, die sich nach dem Bohr’schen Modell auf Kreisbahnen bewegen. Der
so erzeugte Kreisstrom ist abhängig von der Frequenz f bzw. der Geschwindigkeit v der
Elektronen (q = −e):
v
I = qf = q
(3.4.7)
2πR
Für das Dipolmoment gilt somit:
~ = q Af
~ = q(R2 π~n)f · 2 · 1 = 1 qR2 ω
p~m = I A
~
| {z } 2
2
(3.4.8)
ω
~
~ = mR2 ω
Der (Bahn-)Drehimpuls L
~ führt letztendlich auf:
p~m =
3.5
q ~
L
2m
(3.4.9)
Magnetisierung und Suszeptiblität
Als nächstes wollen wir beschreiben, wie ein Magnetfeld auf magnetisierbare Materialien
wirkt. Wir können aus dem Analogon mit dem elektrischen Feld vorhersagen, dass das
13
Material selbst magnetische Eigenschaften erhalten und das Gesamtmagnetfeld verändern
~ welwird. Um diesen Prozess zu beschreiben, verwenden wir die magnetische Erregung H,
che in Kapitel 3 eingeführt wurde.
Legt man ein äußeres Magnetfeld an, werden Dipole innerhalb eines (magnetisierbaren)
Materials ausgerichtet und erzeugt; als Magnetisierung wird die „Dichte“ dieser Dipole
definiert :
X
~ = 1
p~m
(3.5.1)
M
V V
~ ] = [H]
~ = 1 A . Die Magnetisierung ist proportional zur magneDiese hat die Dimension [M
m
tischen Erregung mit der Proportionalitätskonstante χm , die magnetische Suszeptibilität
genannt wird:
~ = χm H
~
M
(3.5.2)
Für das Magnetfeld ergibt sich dementsprechend:
~ = µ0 (H
~ +M
~ ) = µ0 ( H
~ + χm H)
~ = µ0 (1 + χm )H
~ = µr µ0 H
~
B
(3.5.3)
Die Beziehung zwischen relativer Permeabilität µr und Suszeptibilität ist folglich:
µr = 1 + χ m
(3.5.4)
Magnetische Effekte werden durch freie und gebundene elektrische Ströme erzeugt. Freie
Ströme werden durch äußere Spannungen erzeugt, gebundene Ströme finden atomar statt
(siehe Abschnitt 3.4.3). Die atomaren Ströme werden in Berechnungen als Oberflächenströme oder magnetische Dipole verwendet.
Bemerkung: Beim Übergang zwischen einem (magnetisierbaren) Körper und dem Vaku~ = 0 und dem Gauß’schen Satz 1.1.9, dass die Normalkomponente
um folgt aus div B
~ stetig an der Grenzfläche ist.
des Magnetfeldes B
3.6
Arten der Magnetisierung
Die Art der Magnetisierung wird durch die Größe und das Vorzeichen der magnetischen
Suszeptibiltät χm des Materials beschrieben. Diese sagt letztendlich aus, wie stark die
Kräfte durch ein äußeres Magnetfeld auf ein magnetisierbares Medium sind und ob dieses in das Feld hineingezogen oder aus dem Feld herausgestoßen wird. Die Gesamtkraft
auf das Medium erhält man dann als Summe über die Kräfte auf die einzelnen Dipole.
Beim Summieren werden die Dipolmomente, wie aus Gleichung 3.5.1 ersichtlich, mit der
Magnetisierung ersetzt. Man erhält:
~ M
~ · B)
~
F~ = ∇(V
~ = χm H
~ =
Mit M
χm ~
B
µ0
(3.6.1)
erhalten wir:
χm V ~ 2
F~ =
∇B
µ0
14
(3.6.2)
Nun wird zwischen drei verschiedenen Arten der Magnetisierung unterschieden (die Grenzen sind nicht genau festgelegt!):
• Diamagnetismus: χm < 0
In einem diamagnetischen Material werden erst durch das Einwirken eines äußeren
Magnetfeldes magnetische Dipolmomente induziert. Diamagneten erfahren eine Kraft
in Richtung des schwächer werdenden Magnetfeldes.
• Paramagnetismus: χm > 0, |χm | 1
Paramagnetische Materialien enthalten bereits permanente Dipole, die durch das äußere Magnetfeld ausgerichtet werden. Paramagneten erfahren eine Kraft in Richtung
des stärker werdenden Magnetfeldes.
• Ferromagnetismus: χm > 0, |χm | 1
Die vorhandenen permanenten magnetischen Dipole passen sich beim Ferromagneten
noch besser dem äußeren Magnetfeld an und erhalten auch nach dem Entfernen des
Feldes ihre Richtung aufrecht.
Makroskopisch betrachtet besteht der Ferromagnet aus vielen kleinen magnetischen
Domänen, sog. Weiß’schen Bezirken. In so einem Bezirk sind alle Dipole bereits parallel ausgerichtet und sie richten sich alle gleichzeitig nach dem äußeren Magnetfeld aus.
Ferromagneten erfahren durch das äußere Magnetfeld eine Kraft in Richtung des stärker werdenden Magnetfeldes.
Mit steigender Temperatur verliert das Material seine ferromagetischen Eigenschaften
und wird ab der Curie-Temperatur zum Paramagnet.
Die momentane Magnetisierung des Ferromagneten ist von dessen Vorbehandlung abhängig und sie beschreibt die sogenannte Hystereseschleife.
Ist das externe Magnetfeld stark genug, so erfolgt der Durchlauf folgendermaßen: Bei
B = 0 gilt M = 0. Dann wird das äußere Feld langsam aufgedreht und die Magnetisierung verhält sich wie von der „Neukurve“ a gezeigt. Ab einen gewissen Wert des
Magnetfeldes bliebt die Magnetisierung konstant (alle Weiß’schen Bezirke haben die
selbe Orientierung eingenommen → Sättigung).
Wird die Flussdichte nun verringert, so verhält sich die Magnetisierung wie von Kurve
b gezeigt. Wird das externe Magnetfeld abgeschaltet (B = 0), so bleibt im Material
eine permanente Magnetisierung MR übrig. Dreht man die Richtung des Magnetfeldes um, erreicht man wieder eine Sättigung. Bei erneutem Umdrehen verhält sich das
Magnetfeld wie bei Kurve c.
Abbildung 3.7: Die Hystereseschleife bzw. die Magnetisierung in Abhängigkeit vom äußeren Magnetfeld(4)
15
Abbildungsquellen
(1) Hugel, Thorsten (2013): Vorlesungsskript Experimentalphysik 2, München
(4) Demtröder, Wolfgang (2009): Experimentalphysik 2, Springer-Verlag, Berlin Heidelberg
(6) en.wikipedia.org/wiki/Magnetic_dipole
(17) upload.wikimedia.org/wikipedia/commons/thumb/a/a3/
Gerader_leiter.svg/220px-Gerader_leiter.svg.png
16