Gruppe A - Mathematik-Wettbewerb des Landes Hessen
Werbung
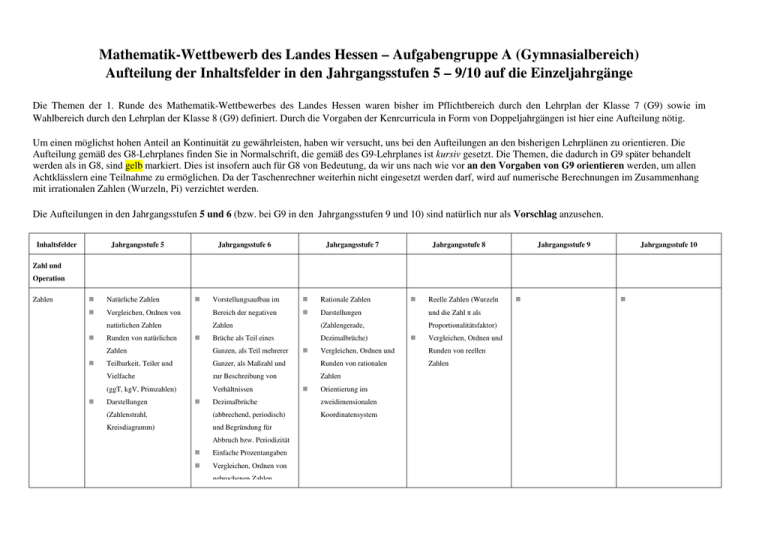
Mathematik-Wettbewerb des Landes Hessen – Aufgabengruppe A (Gymnasialbereich) Aufteilung der Inhaltsfelder in den Jahrgangsstufen 5 – 9/10 auf die Einzeljahrgänge Die Themen der 1. Runde des Mathematik-Wettbewerbes des Landes Hessen waren bisher im Pflichtbereich durch den Lehrplan der Klasse 7 (G9) sowie im Wahlbereich durch den Lehrplan der Klasse 8 (G9) definiert. Durch die Vorgaben der Kenrcurricula in Form von Doppeljahrgängen ist hier eine Aufteilung nötig. Um einen möglichst hohen Anteil an Kontinuität zu gewährleisten, haben wir versucht, uns bei den Aufteilungen an den bisherigen Lehrplänen zu orientieren. Die Aufteilung gemäß des G8-Lehrplanes finden Sie in Normalschrift, die gemäß des G9-Lehrplanes ist kursiv gesetzt. Die Themen, die dadurch in G9 später behandelt werden als in G8, sind gelb markiert. Dies ist insofern auch für G8 von Bedeutung, da wir uns nach wie vor an den Vorgaben von G9 orientieren werden, um allen Achtklässlern eine Teilnahme zu ermöglichen. Da der Taschenrechner weiterhin nicht eingesetzt werden darf, wird auf numerische Berechnungen im Zusammenhang mit irrationalen Zahlen (Wurzeln, Pi) verzichtet werden. Die Aufteilungen in den Jahrgangsstufen 5 und 6 (bzw. bei G9 in den Jahrgangsstufen 9 und 10) sind natürlich nur als Vorschlag anzusehen. Inhaltsfelder Jahrgangsstufe 5 Jahrgangsstufe 6 Jahrgangsstufe 7 Jahrgangsstufe 8 Jahrgangsstufe 9 Jahrgangsstufe 10 Zahl und Operation Zahlen Natürliche Zahlen Vorstellungsaufbau im Rationale Zahlen Vergleichen, Ordnen von Bereich der negativen Darstellungen und die Zahl π als natürlichen Zahlen Zahlen (Zahlengerade, Proportionalitätsfaktor) Runden von natürlichen Ganzen, als Teil mehrerer Teilbarkeit, Teiler und Vielfache (ggT, kgV, Primzahlen) Brüche als Teil eines Zahlen Darstellungen Dezimalbrüche) Reelle Zahlen (Wurzeln Vergleichen, Ordnen und Vergleichen, Ordnen und Runden von reellen Ganzer, als Maßzahl und Runden von rationalen Zahlen zur Beschreibung von Zahlen Verhältnissen Orientierung im Dezimalbrüche zweidimensionalen (Zahlenstrahl, (abbrechend, periodisch) Koordinatensystem Kreisdiagramm) und Begründung für Abbruch bzw. Periodizität Einfache Prozentangaben Vergleichen, Ordnen von gebrochenen Zahlen (gewöhnliche Brüche, Dezimalbrüche) Runden von Dezimalbrüchen Darstellungen (Zahlenstrahl, Kreisdiagramm) Zahlen Natürliche Zahlen Vergleichen, Ordnen von natürlichen Zahlen Runden von natürlichen Vorstellungsaufbau im Rationale Zahlen Bereich der negativen Darstellungen Zahlen (Zahlengerade, Brüche als Teil eines Dezimalbrüche) Zahlen Ganzen, als Teil mehrerer Darstellungen Ganzer, als Maßzahl und (Zahlenstrahl, zur Beschreibung von Kreisdiagramm) Verhältnissen Zahlen Orientierung im zweidimensionalen Koordinatensystem Einfache Prozentangaben Vergleichen, Ordnen von gebrochenen Zahlen (gewöhnliche Brüche, Dezimalbrüche) Runden von Dezimalbrüchen Teilbarkeit, Teiler und Vielfache (ggT, kgV, Primzahlen) Runden von rationalen (abbrechend, periodisch) Abbruch bzw. Periodizität Vergleichen, Ordnen und Dezimalbrüche und Begründung für Darstellungen (Zahlenstrahl, Kreisdiagramm) Reelle Zahlen (Wurzeln und die Zahl π als Proportionalitätsfaktor) Vergleichen, Ordnen und Runden von reellen Zahlen Operationen und ihre Grundrechenarten und Rechengesetze für Eigenschaften natürliche Zahlen Strategien zum vorteilhaften Rechnen Grundrechenarten und Rechenverfahren, Rechengesetze und deren Rechengesetze und deren gebrochene Zahlen Verknüpfungen im Bereich Verknüpfungen im Grundaufgaben der der rationalen Zahlen Bereich der reellen Zahlen Bruchrechnung und der Prozentrechnung Rechenverfahren, Rechengesetze für Grundaufgaben der Klammern, Binome Prozent- und Zinsrechnung Potenzen mit rationalen Prozentrechnen mit erhöhtem und Exponenten Terme und Variable Rechenverfahren, vermindertem Grundwert Operationen Grundrechenarten und Grundrechenarten und Prozente von Prozenten Rechenverfahren, und ihre Rechengesetze für Rechengesetze für Rechengesetze und deren Rechengesetze und deren Eigenschaften natürliche Zahlen gebrochene Zahlen Verknüpfungen im Bereich Verknüpfungen im Bereich Strategien zum vorteilhaften Rechnen Grundaufgaben der Bruchrechnung und der der rationalen Zahlen Prozentrechnung der reellen Zahlen Grundaufgaben der Klammern, Binome Prozent- und Zinsrechnung Potenzen mit rationalen Prozentrechnen mit erhöhtem und Exponenten Terme und Variable vermindertem Grundwert Prozente von Prozenten Grundfiguren Raum und Form Ebene Figuren Grundfiguren (Quadrat, Symmetrieeigenschaften Rechteck, Dreieck, Kreis) (Achsen- und und zusammengesetzte Drehsymmetrie) von Flächen Grundfiguren Konstruktion von Figuren (Parallelogramm, Trapez, Raute, Drachen, Kreis) Haus der Vierecke Konstruktionen mit und Mustern Zeichengeräten und Kartesisches dynamischer Koordinatensystem im Geometriesoftware ersten Quadranten Symmetrieeigenschaften von Figuren Kartesisches Koordinatensystem in allen vier Quadranten Ebene Figuren Grundfiguren (Quadrat, Symmetrieeigenschaften Rechteck, Dreieck, Kreis) (Achsen- und und zusammengesetzte Drehsymmetrie) von Flächen Grundfiguren Konstruktion von Figuren Grundfiguren Kreis (Parallelogramm, Trapez, Konstruktionen mit Raute, Drachen) Zeichengeräten und Haus der Vierecke dynamischer Konstruktionen mit Geometriesoftware und Mustern Zeichengeräten und Kartesisches dynamischer Koordinatensystem im Geometriesoftware ersten Quadranten Symmetrieeigenschaften von Figuren Kartesisches Koordinatensystem in allen vier Quadranten Körper Grundkörper (Quader, Würfel) und Beschreibung von Beschreibung von Volumen und Volumen und Oberflächeninhalt beim Oberflächeninhalt der Grundkörper Kreiszylinder) zusammengesetzte Körper Grundkörper (Prisma, Modelle, Schrägbilder und Grundkörper (Pyramide, Kegel, Kugel) Körper aus der Technik und der Lebensumwelt Beschreibung von Prisma Volumen und Modelle, Schrägbilder und Oberflächeninhalt bei Pyramide, Kegel, Kugel Netze bekannter Körper Netze der Grundkörper Modelle, Schrägbilder und Netze bekannter Körper Körper Grundkörper (Quader, Würfel) und zusammengesetzte Körper Grundkörper (Prisma, Kreiszylinder) Beschreibung von Beschreibung von Volumen Volumen und und Oberflächeninhalt der Oberflächeninhalt beim Grundkörper Prisma Grundkörper (Pyramide, Kegel, Kugel) Körper aus der Technik und der Lebensumwelt Beschreibung von Volumen und Modelle, Schrägbilder und Netze der Grundkörper Modelle, Schrägbilder und Oberflächeninhalt bei Netze bekannter Körper Pyramide, Kegel, Kugel Modelle, Schrägbilder und Netze bekannter Körper Beziehungen zwischen Fachbegriffe parallel, senkrecht, Abstand geometrischen Bewegungen von Figuren: Drehungen, Spiegelungen, Fachbegriffe (Kongruenz, Symmetrie) Verschiebungen Objekten Satzgruppe des Pythagoras Trigonometrischen und seine Umkehrung Beziehungen (sin, cos, einschließlich tan) bei rechtwinkligen exemplarischer und allgemeinen vollständiger Beweise Dreiecken Satz des Thales Ähnlichkeit, zentrische Streckungen, Strahlensätze Beziehungen zwischen Fachbegriffe parallel, senkrecht, Abstand geometrischen Bewegungen von Figuren: Drehungen, Spiegelungen, Fachbegriffe (Kongruenz, Symmetrie) Verschiebungen Objekten Satzgruppe des Pythagoras und seine Beziehungen (sin, cos, tan) Umkehrung einschließlich bei rechtwinkligen und exemplarischer allgemeinen Dreiecken vollständiger Beweise Satz des Thales Ähnlichkeit, zentrische Streckungen, Strahlensätze Größen und Messen Umgang Größen mit Größenvorstellungen Einheitsquadrat, Zusammengesetzte Figuren Größen von Winkeln Einheitswürfel Repräsentanten, (Minuten, Sekunden) Winkelsummensatz und die Schätzungen und Winkelsätze an Geraden- Überschlagsrechnungen kreuzungen Runden Umrechnung von Größen Vorsilben von Einheiten Trigonometrischen Umgang mit Größen Größenvorstellungen Einheitsquadrat, Zusammengesetzte Figuren Größen von Winkeln Einheitswürfel Messvorgänge (Minuten, Sekunden) Repräsentanten, Winkelsummensatz und die Schätzungen und Winkelsätze an Geraden- Überschlagsrechnungen kreuzungen Runden Umrechnung von Größen Vorsilben von Einheiten Länge Masse/Gewichte von Dreieck, Oberflächeninhalt beim Dreiecken und Vielecken Währung/Geld Parallelogramm, Trapez, Prisma (Anwendungen aus Zeitspanne Raute, Drachen, Kreis Winkel Flächeninhalt und Umfang Oberflächeninhalt bei von Quadrat und Rechteck Pyramide, Kegel, Volumen und Zylinder, Kugel Flächeninhalt und Umfang Volumen und Berechnungen in Technik und Physik) Volumen und Oberflächeninhalt der Grundkörper Messvorgänge Länge Masse/Gewichte Währung/Geld Zeitspanne Winkel Grundkörper Flächeninhalt und Umfang Flächeninhalt und Umfang von Quadrat und Rechteck von Dreieck, Volumen und Parallelogramm, Trapez, Oberflächeninhalt der Raute, Drachen Flächeninhalt und Umfang Dreiecken und Vielecken Volumen und (Anwendungen aus Oberflächeninhalt beim Technik und Physik) Prisma Berechnungen in vom Kreis Volumen und Oberflächeninhalt bei Pyramide, Kegel, Zylinder, Kugel Funktionaler Zusammenhang Zuordnungen Grundvorstellungen zu Proportionale und Grundvorstellungen zu und ihre Darstellungen Zuordnungen von Größen antiporportionale nicht-proportionalen Darstellung der Zuordnungen und ihre funktionalen Zuordnungen in Eigenschaften Zusammenhängen Schaubildern und Tabellen Dreisatzmethoden und in sprachlicher Form Darstellung der Zuordnungen in proportionalen und sprachlicher, tabellarischer antiporportionalen oder graphischer Form Darstellung der Zuordnungen in sprachlicher, tabellarischer und graphischer Form Zuordnungen und ihre Darstellungen Grundvorstellungen zu Proportionale und Grundvorstellungen zu Zuordnungen von Größen antiporportionale nicht-proportionalen Darstellung der Zuordnungen und ihre funktionalen Zuordnungen in Eigenschaften Zusammenhängen Schaubildern und Tabellen Dreisatzmethoden und in sprachlicher Form Darstellung der Zuordnungen in proportionalen und sprachlicher, antiporportionalen tabellarischer oder Zuordnungen in graphischer Form Darstellung der sprachlicher, tabellarischer und graphischer Form Funktionen und Gleichungen Lösen von linearen Gleichungen Vergleich des Vorgehens Lineare Funktionen und ihre Eigenschaften beim Lösen von linearen Gleichungen Lösen von Ungleichungen Lösen von quadratischen Darstellung von Funktionen Lösen von linearen 2×2- (Funktionsgleichung, Gleichungssystemen Tabelle, Graph) Einfache Potenzfunktionen Exponentialfunktionen Sinusfunktion und ihre wesentlichen Eigenschaften Gleichungen Darstellung von Funktionen (Funktionsgleichung, Tabelle, Graph) Funktionen und Gleichungen Lösen von linearen Gleichungen Vergleich des Vorgehens beim Lösen von linearen Lösen von quadratischen Einfache Potenzfunktionen Gleichungen Exponentialfunktionen Lösen von linearen 2×2- Sinusfunktion und ihre Gleichungssystemen Gleichungen Lineare Funktionen und wesentlichen Eigenschaften Darstellung von ihre Eigenschaften Funktionen Funktionen Lösen von Ungleichungen (Funktionsgleichung, (Funktionsgleichung, Tabelle, Graph) Tabelle, Graph) Daten und Zufall statistische Umfragen und Erhebungen Darstellung von Daten in Erhebungen und (Planung, Durchführung Diagrammen (Boxplot, ihre und statistische Säulendiagramm, Auswertung Auswertung) Kreisdiagramm) und Kenngrößen (Häufigkeiten, Median, arithmetisches Tabellen Lage- und Streumaße Darstellung von Daten in Mittel, Spannweite) Darstellung von Daten (Listen und Diagramme) statistische Umfragen und Erhebungen Erhebungen (Planung, Durchführung Diagrammen (Boxplot, und ihre und statistische Säulendiagramm, Auswertung) Kreisdiagramm) und Kenngrößen (Häufigkeiten, Tabellen Auswertung Median, arithmetisches Mittel, Spannweite) Darstellung von Daten Lage- und Streumaße Darstellung von (Listen und Diagramme) Umgang mit dem Zufall Zufallserscheinungen in alltäglichen Situationen Verschiedene Wahrscheinlichkeitsbegriff Zufallsexperimente Vorstellungen vom Zweistufige Mehrstufige Zufallsexperimente Baumdiagramme und Vierfeldertafeln Pfadregeln Zweistufige Absolute und relative Häufigkeiten Umgang mit dem Zufall Zufallserscheinungen in alltäglichen Situationen Verschiedene Zufallsexperimente Vorstellungen vom Wahrscheinlichkeitsbegriff Absolute und relative Häufigkeiten Baumdiagramme und Vierfeldertafeln Pfadregeln Mehrstufige Zufallsexperimente