Statik - Institut für Technische Verbrennung
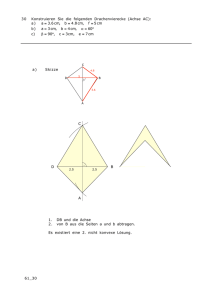
Werbung

LEHRSTUHL UND INSTITUT
für Technische Mechanik
Prof. Dr.-Ing. Norbert Peters
Templergraben 64, 2. Etage
Aufgab ensammlung Mechanik
(Statik, Festigkeitslehre, Dynamik)
für
Elektrotechniker
In der Üb.ttrg Mechanik wird eine Auswahl der a-Aufgaben vorgerechnet, die zugehörigen
b-Aufgaben behandeln jeweils den gleichen Stoff. Die Beschäftigung mit den nicht vorgerechneten Aufgaben dient der Festigung und Überprüfung des Wissensstandes. Zusätzlich
zu der "großen" Ubung werden "Gruppenübungen" angeboten, in denen aufFragen besser
eingegangen werden ka.nn. Für ausländische Kommilitonen findet ein "Ausländerseminar"
statt. Ubungsklausuren bereiten gezielt auf die Diplomvorprüfung vor. Individuelle Beratung wird besonders in den Sprechstunden der studentischen Hilfskräfte angeboten. Die
Sprechstundenzeiten werden durch Aushang bekanntgegeben.
Winkel und Längen können aus den maßstäblichen Skizzen entnommen werden.
Statik
Aufgabe O: Vorübung zur Vektorrechnung
d;; i :7r2,3r4 durch a1 : 5,6m1 a1 : f15"1
oz :8m; 9z: -10"1 as: -8,8m; og : -175o; Q4x: -4r652rn;
a4s : -12,78m'
Gegeben: Vier ebene Vektoren
Gesucht: a) resultierender Vektor
b) Vektor 6: ü - dz
r-: Dä;, i :1,2,3,4
c) Skalarprodukt s : d.r .d,z
d) Vektorprodukt 6: d,r x dz
e) Tensorprodukt n: drdz
f) Zerlegung des Vektors r- nach den Richtungen 01
g) Zerlegung des Vektors r- nach den Richtungen a1
oa : 90"'
- 0o;
- 0o;
az :60"
oz :60";
Aufgabe la:
In einem Punkt P eines starren Körpers greifen 6 Kräfte so a.n, da3 der Körper sich im
Gleichgewicht befindet ("als ob überhaupt keine Krdfte angreifen würden"). Von den
6 Kräften sind 4 vorgegeben, von den beiden anderen sind die Richtungen I, II (nicht
Richtungssinn) vorgeschrieben.
Gegeben: Kraft in der Zugfeder I : 22N; cr : 11o;
Ä durch die Komponenten C :14. rtX und
B: -70N;
-D : -14N
F
:
Gesucht: a) Ä
b) Kraft von der Feder auf den Körper
c) Krrifte auf die Fbder
d) Resultierende der vorgegebenen Krdfte
e) Zerlegung der Resultierenden nach den Richtungen I und II
f) Zerlegung der Resultierenden nach den Richtungen I, II und
g) Resultierende der beiden nicht gegebenen IGäfte
h) die beiden nicht gegebenen Krdfte
t'
I
I
I
I
I
I
!
III
34N;
Aufgabe lb:
In einem Punkt eines Körpers, der sich im Gleichgewicht befindet, greifen 5 Krdfte ar), von
denen drei gegeben sind.
Gegeben: Kr
- 500N;
K2
- -520N;
Ks
-
800N
Gesucht: a) Resultierende der gegebenen Kräfte
b) Zerlegung der Resultierenden nach den Richtungen I und II
c) Resultierende der nicht gegebenen Krdfte, die die Richtungen I und
d) die nicht gegebenen Krdfte
II
haben
Aufgabe 2a:
Die "gewichtslosen" Seile 1,2,3,4 und 5 sind bei A und B verknotet
bei C und D mit
dem Fundament verbunden- Die Seile 1 und 2 werden über die
'nd
Rollen
6 und Z umgelenkt.
Das Seil t hzilt ein Gewicht G1, das Seil 2 wird durch einen Flaschenzug
so gespannt, daß
die skizzierte Lage eingenommen wird.
Gegeben: G1 :2b0N; Gewicht der Rollen 6,? und g: Gn : 100N
maßstäbliche Skizze M
:
1:10
Gesucht: u) Gz
b) seilkräfte 4 und 5 als Funktion des winkels 0 ( c < g0"
+'
Aufgabe 2b:
Die "gewichtslosen" Seile 1, 2 und 3 sind bei A verknotet und bei B und C gehalten.
System wird über einen Flaschenzug belastet.
Gegeben: Gs -- 350N; Gewicht der Rollen Gn
maSstäbliche Skizze M : 1:20
:
120N
Gesucht: a) Seilkräfte für a : 30"
b) Seilkräifte 2 und 3 als Funktion des Winkels 0 ( o <
90o
Aufgabe 3a:
Zwei schwere Scheiben 1 und 2 sind bei C gelenkig verbunden. Die Scheibe 1 ist bei A fest
eingespa^nnt, die Scheibe 2 stützt sich bei B reibungsfrei auf. An der Scheibe 2 greift bei
D das Moment Mo *.
Gegeben: G1 :
:500N; Me maßstäbliche Skizze M : 1:10
800N;
Gz
160N.m
Gesucht: Auflagerreaktionen und Gelenkkraft
+'
Aufgabe 3b:
Zwei Balken 1 und 2 sind bei C gelenkig verbunden und bei A bzw. B gelagert. Am Balken
1 greifen die Kräif,te Ifi und K2, atn Balken 2 die Kraft Ks und das Moment M1 an.
Gegebenz
Kt - Kz - 500N; Kt - 400N;
maßstäbliche Skizze M
:
1:10
Gesucht: Auflagerreaktionen und Gelenkkraft
,////t
M1
-
80N.m
Aufgabe 4a:
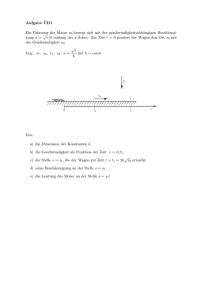
Ein Wagen mit dem Gewicht G1 und dem Schwerpunkt ,S befindet sich auf einer schiefen
Ebene. Das Gewicht der Räder ist Gzbzw. Gs. Der Wagen wird über ein Seil ,S la^ngsam
nach oben gezogen.
Gegebeni G1 :2
.
10aN;
Gz
:
maßstäbliche Skizze M
Gs
:
: 500N; a :20o
1:100
Gesucht: a) Kräfte auf die Räder 2 und 3
b) Kräfte auf den Wagenkasten 1
Aufgabe 4b:
Eine schwere Scheibe
I
wird von drei Stäben 2, 3 und 4 gehalten und durch die Kraft
belastet.
Gegeben: G
:1000N; F :
1500N
maßstäbliche Skizze M
:
1:10
Gesucht: Stabkräfte (ZuS- oder Druckstäbe?)
^F
Aufgabe 5a:
Gegeben: maßstäbliche Skizzen M
:
1:100
Gesucht: Schwerpunkte
drei Massenpunkte
/\
,r\
mz
-
\
4mr = 5kg
drei Süibe
Dreieckfläche
4kg
\
.$
m: = 2kg
Aufgabe 5b:
Gegeben: maßstäbliche Skizzen M
:
1:100
Gesucht: Schwerpunkte
rn4
/\
vier Massenpunkte
\
/
mr = 2kg
vier stäbe
Viereckfläche
= lkg
- \-l
\
I
_
-
I
rnt=5kg
rry = 3kg
Aufgabe 6a:
Gegeben: maßstäblich skizzierte Flächen M
Gesucht: Schwerpunkte
:
l:100
Aufgabe 6b:
Gegeben: maSstäblich skizzierte Flächen M
Gesucht: Schwerpunkte
:
1:100
Aufgabe 7a:
Ein Lastzug ist auf einer Steigung abgestellt. Der Zugwagen ist an der Hinterachse gebremst; die Bremsen des Anhängers sind gelöst.
Gegeben2 G1 :
128kN;
Gz
:20kN;
Gs
:40kN;
LKW, Schwerpunkt S);
mäßstäbliche Skizze M : l:100
Gesucht: Auflagerreaktionen bei A, B, C und D
G
:
50kN
(:
Eigengewicht des
Aufgabe 7b:
Ein abgewinkelter Balken wird durch zwei Kräfte und ein Moment belastet.
Gegeben:
r'r:Fz -1200N; M:400N.m
maßstäbliche Skizze M : 1:10
Gesucht : Aufl agerreal<tionen
'/////.
Aufgabe 8a:
Ein Ausleger besteht aus den schweren Balken 1 und 2 und den gewichtslosen
Stäben 3
und 4. Der Balken hält ein Gewicht G.
Gegeben: G :200N;
Gr:200N; Gz:500N
maSstäbliche Skizze M : 1:10
Gesucht: a) Auflagerreaktionen und Stabkräfte
b) Innere Kraft in den Schnitten BE und F_F
Aufgabe 8b:
Ein schwerer Quader I und ein schwerer Balken 2 sind bei C gelenkig verbunden. Der
Quader stützt sich bei Ä und B reibungsfrei gegen das F\rndarnent, der Balken wird bei
D von einem festen Auflager gehalten.
Gegeben:
G1:600N;
Gz -- 400N
md,ßstäbliche Skizze M: 1:10
Gesucht: Aufl agerreafttionen und Gelenkkraft
Aufgabe 9a:
Ein Rahmet
I
(q - SON/m) ist bei Ä und B gelagert und häIt eine Rolle 2. Über diese
Rolle ist ein Seil geführt, welches um den Bolzen bei A geschlungen ist und bei C an einem
Quader 3 (p - 600N/m2) befestigt ist. Der Quader wird von einem Stab 4 und dem Lager
D gehalten.
Gegeben: maßstäbliche Skizze M:1:10
Gesucht: a) Kräfte auf den Balken 1, den Bolzen Ä und die Rolle
c) Kräfte auf den Quader 3
c) Schnittlasten für den Rahmen 1
2
Aufgabe 9b:
Ein Rahmen 1 (Gewicht je Meter Länge p :20N /m) ist bei Ä und B gelagert. Ein Seil
ist über die Rolle 2 (Gewicht: Gz - 200N) geführt und arn Bolzen Ä befestigt. Das Seil
hält ein Gewicht Gs : f50N.
Gegeben: maßstäbliche Skizze M
:
1:100
Gesucht: a) Kräfte auf Rolle 2, Seil, Bolzen Ä und Balken
b) Schnittlasten für den Rahmen
B
/./././
^
1
-l
t)
+-
Aufgabe
1Oa:
Ein schwerer Balken I ist über zwei ("gewichtslose") Stützen mit einer kleinen Rolle und
dem F\rnda,rrent verbunden. Bei B greift eine zeiülich veränderliche Kraft f'(t) an. Die
Haftreibungszahl bei A ist p - 0,5; die Gleitreibungszahl pc :0,3.
Gegeben: G1 :400N;
f'(t)
maßstäbliche Skizze M
:
1:10
Gesucht: a) Auflagerreaktion bei A als F\rnktion der Zeit
b) in welchen Zeitintervallen bewegt sich das System?
+'
//,//,/,/,/,/,/,/.
F
N
101
F(r)
Aufgabe
1Ob:
Ein Tisch mit dem Gewicht G und dem Schwerpunkt S wird von einer Kraft .F langsam
über eine Ebene gezogen.
Gegeben: G :500N; FG :0,3
maßstäbliche Skizze M
:
1:10
Gesucht: a) erforderliche Kraft F
b) Wie groß darf p6 höchstens werden, ohne daß der Tisch kippt?
?S
I
I
I
I
Aufgabe 11a:
Eine (gewichtslose) Greifzange häIt ein Gewicht
Gegeben: maßstäbliche Skizze M
:
Gs:500N.
1:20
Gesucht: a) Kräfte auf die Teile 1, 2,3, 4 und 5
b) erforderlicher Haftreibungskoeffizient perr
c) Wie kann die Konstruktion geändert werden, wenn die Reibung nicht ausreichen würde, das Gewicht zu halten?
+'
Aufgabe llb:
Eine Bremse besteht atrs einenr Biigei 1, an cierrr ticr Brernsklotz 2 befestigi isb. Die
BrernskraJt zrvischen \\telle 3 uncl Brerrrsklotz 2 soll 1;rrnktförmig bei Ä zrngreifen.
Gegeben:
/:40cm;
T':10crn; p:0,5
Gesucht: a) rvelches Gervicht G kann bei a : 60cm und -P: 200N gehalten rverden?
b) weichen Absband a muß das Auflager C mindestens haben, damit Selbsthemmung auflritt (.t' :0!X
l-
Aufgabe 12a:
Ein schwerer Balken 1 ist bei Ä gelagert und stützt sicir bei B mit Reibung (ohne zu
rutschen) gegen das Fundament. Der Baiken wird von einem durch das Gewicht G2 gespannten Seilzug belastet.
Gegeben: G1 :160N; / - 0,8m; p -- 0,2
maßstäbliche Skizze M : 1:10
Gesucht: a) Wie groß muß Gz mindestens sein?
b) Wie groß darf Gz höchstens sein?
c) Längskraft-. Querkraft- und Biegemomentenverlauf f:ür Gz: 100N
+'
Aufgabe 12b:
Ein schwerer Balken 1 ist bei .A gelagert und stützt sich bei B mit Reibung gegen das
F\rndament. Am Balken ist bei C ein "gewichtsloser" Hebel 2 a^ngeschweißt, der eine Last
G3 hält.
Gegeben: G1 :200N; Gs
:100N;
I:
lm;
Gesucht: a) Wie groß darf a höchstens sein?
b) ,-, Q- und M-Verlauf für a : 0,3m
ö
: 0,3m; p :
0,3
Aufgabe 13a:
Der maßstäblich skizzierte Gerberträger I ist bei .A, B und C so gelagert, daß er in Ruhe
ist' Der Träger wird durch einen Seilzug belastet, der das Gewicht Gz hält. Die Haftreibungszatrl bei C ist angegeben.
Gegeben: G2 :400N; Fo : 0,2
Gesucht: eine obere Schranke für Gz
7mz
A
7Z
B
7////,
C
Aufgabe 13b:
Für den skizzierten Gerberträger ist die Auflagerreaktion auszurechnen. Das Gewicht
Trägers ist zu vernachlässigen.
Gegeben: maßstäbliche Skizze M
:
des
1:10
Gesucht: Auflagerreaktion bei A
a) durch Gleichgewichtsaussagen
b) durch das Prinzip der virtuellen Arbeit (mit Skizze der gewählten virtuellen
Verschiebung!)
Aufgabe 14: (Weihnachtsaufgabe)
Ein Weihnachtsbaum mit dem spezifischen Gewicht 7 steht auf dem Boden.
Gegeben: Höhe I1; Gewicht des Sterns G*; r(0) :10
Gesucht: Radius des Stammes als Funktion der Koordinate r so, da3 die Beanspruchung
des Stammes überall gleich ist, d.h. L(a)lA(r) -oznr: konst. gilt.
Anmerkung: Das Gewicht der Aste, der Zweige und der Nadeln ist zu vernachlässigen
("saurer Regen"!), ebenso das Gewicht der Geschenke (Vater Beamter!!).
+'
7///////////////////////////////n
Festigkeitslehre
Aufgabe 15a:
Der ebene Spannungszustand im Punkt C eines Bleches ist gegeben durch die Spannungsvektoren in den zueina^nder senkrechten Schnitten A, und Ar.
Gegebeni
or:200N/mm2; ty :
100N
(Beträge, Richtungen nach
l^ ';
rxs:80N/mm2
Skizze), a:
45o
Gesucht: a) Spannungsvektor im Schnitt Äo im Punkt C
b) Spannungstensor
c) Hauptspannungen und H auptspannungsrichtungen
d) Mocimale Schubspannung und zugehörige Richtung
Aufgabe 15b:
Der ebene Spa,nnungszustand im Punkt C eines Bleches ist gegeben durch die Spannungsvektoren in den zueinander senkrechten Schnitten A, und Ao.
Gegebeni
or:200N/mm2;
oy
:
100N
(Beträge, Richtungen nach
/*ot';
rxy:50N/mm2
Skizze), a:45"
Gesucht: a) Spannungsvektor im Schnitt /o im Punkt C
b) Spannungstensor
c) Hauptspannungen und Hauptspannungsrichtungen
d) Maximale Schubspannung und zugehörige Richtung
Aufgabe 16a:
Der Spannungszustand im Punkt Ä auf der Oberfläche einer Welle soll durch Dehnmeßstreifen (DMS) ermittelt werden. Hierzu wurden drei DMS aufgeklebt ("45"-Rosette").
Bei der Belastung der Welle wurden die Dehnungen e1 : -1,8.10-3; ez : *3,6.10-3 und
: -\,2 '10-3 abgelesen.
Gegeben: E-2,1 .105N/mm21 u:0,3
eg
Gesucht: a) Spannungstensor
b) Größe und Richtung der max. Normalspannung
c) Größe und Richtung der max. Schubspannung
2
Aufgabe
LGb:
Ein Blech steht unter der Wirkung eines konstanten Spannungszustandes. Die Abstandsänderung der Punkte A, B und C vom Punkt D gegenüber dem unbelasteten Zustand ist
gemessen worden.
Gegeben;
a:40cm; ö: 60cm; c : 40cm; Ac : 2. 10-2cm; A6:
Ac : 4. 10-2cm; E : 2,!. 107N/cm2; u : 0,8
Gesucht: a) Spannungstensor
b) H auptspannungsrichtungen
c) max. Schubspannung
3. 10-2cm;
Aufgabe 17a:
Eine Fliehkraftbremse besteht aus einem homogenen Stahlstab (Querschnittsfläche Ä), der
sich um das Lager B dreht und aus einem feststehcndcn Schleifring.
Gegeben: I :
20cm; R: 20,01cm; E: 2. 107N l"';
p :7,85glcm3
Gesucht: Bei welcher Drehzahl beginnt die Bremsrvirkung?
Anmerkung: Hier gilt für die Längsbelastung [N/*] Ä(r)
w:
Q:2irn
: pAu2r mit
Aufgabe 17b:
Zwei homogene Statrlstäbe
Gewicht Gs.
Gegeben:
I
und 2 sind untereinander gelenkig verbunden und halten ein
- 2m; lz :3m; ?:78,5kN/*t;
E :2. 107N/cm2
11
Gesucht: Wie groß ist das Gewicht Gs
mr.
At:1cm2;
Az:2c131121
wählen, damit die Absenkung des Punktes Ä
doppelt so groß wird, wie die Absenkung des Punktes Ä durch das Eigengewicht
der Stäbe allein?
T11
J,I
L2
_L
I,
Aufgabe 18a:
Drei elastische Stäbe 1, 2 und 3 halten einen Knoten D, an dem die Kraft
Gegeben:
K :2000N;
h: Izlrt:
ls
:2m; E.A:2.10?N
Gesucht: a) Stabkräfte Sr, ,Sz und ^9g
b) Verschiebungsvektor des Punktes D
K
angreift.
Aufgabe 18b:
Ein Fachwerk besteht aus drei gleichen elastischen Stäben 1, 2 und 3. Der Stab 3 wird um
A? erwärmt.
Gegeben:
l:lm; d:20mm; d:L2.L0-6K-L, f :0,72mm; E:2,!.105N/mm2
Gesucht: a) Temperaturerhöhung a?, die zur Montage erforderlich ist
b) Stabkräfte nach der Montage, wenn Stab 3 wieder die Ausgangstemperatur
hat (AT : 0)
4sol
D,
D
4so
Aufgabe 19a:
Ein starrer Klotz mit dem Gewicht G hängt an drei Seilen.
Gegeben: Querschnitt der Seile Äs
- 1cm2; Es :5. 105N/cm2; /s :
0,5m;
G-12000N
Gesucht: Spa,nnungen in den Seilen, wenn beim Durchschneiden des Seils 2 die Seile 1
und 3 sich um A :0,5cm verlängern
I,
Aufgabe 19b:
Ein starrer Quader mit dem Gewicht G ist bei B drehbar gelagert und wird von zwei
Stäben gehalten.
Gegeben: As
:0,1cm2; E :2,L. 105N/mm2; G :
8200N
Gesucht: Spannungen in den Stäben, wenn beim Durchschneiden des Stabes l- im Stab 2
eine Dehnungsänderunl Lez: 2 - 10-3 gemessen wird.
g
Aufgabe
2Oa:
Ein langer, dünnwandiger Druckkessel mit der Wandstärke s
Innendruck p; : 41ba"r; der Außendruck beträgt po : 105Pa.
Gegeben:
d: lm;
I
: 8m;
E
:
1cm steht unter einem
- 2,!. 105N/mm2; v :0,8
Gesucht: a) Spannungszustand im Punkt A
b) Max. Schubspanmrng im Punkt A
c) Anderung des Durchmessers
\
\
-oA
d
t\
I
lt'
//
'./
m,
Aufgabe
2Ob:
Ein langer, dünnwandiger Kessel wird durch den Innendruck von 25bar bei einem Außendruck von lbar belastet. Die zulässige Schubspannung beträgt rz..t:50N/mm2.
Gegeben: d :400mm
Gesucht: erforderliche Wandstdrke
14
I
I
.l
/
\
\
V
/
Aufgabe 21a:
Ein Rekla,sreschild I ist bei B mit einem täger 2 mit Rechteckquerschnitt verschweißt.
Der täger ist bei A im Fundament eingespannt. Das Schild hat ein Gewicht G1 und wird
zusätzlich durch Winddruck p belastet. Das Gewicht des Trägers und der Winddruck auf
den Träger sind zu vernachldssigen.
Gegeben: G1 :750N;
p: 150N/m2; a:5cm; ö: 6cm; c:
d:200cm; I:200cm
Gesucht: Im gefährdeten Querschnitt bei A
a) maximale Normalspannung
b) maximale Schubspannung
BECKERS
I
I
PILS
I
150cm;
Aufgabe 21b:
Gegeben
ist eine Schraubzwinge aus Flacheisen. Die zulässige Längsspannung im Bügel
beträgt ozrr
:
200N/mm2.
Gesucht: ma>cimale Klemmkraft F
b:12
A
L-<l
Ln
,run
Aufgabe 22a:
Ein Balken 1 r,vircl von drei Stüben '). 3 uncl
Temperatur im Stab 3 um 60Ii erhöht.
Gegeben:
E1I1: 107N . cm2 i
as : 12'10-6-I(-1
Gesucht: Stabkrdfte
Dz
:
4 vorspannungsfrci
EzAz
gclrrilterr. D;rrrn rvir.il clic
- Ds- Da:2.106N; /:0.2rrr:
Aufgabe 22b:
Ein abgewinkelter Balken
I ist bei Ä fest eingespa^nnt und wird bei B vorspannungsfrei
von zwei gleichen Stäben 2 und 3 gehalten. Dann greift bei C die Kraft
Gegeben;
a:500mm; l: O00mm; E..I:
F: 50N
10eN .
Gesucht: a) Stabkräfte
b) Verschiebungsvektor des Punktes C
F an.
mm2; E. A: 2. 10aN;
Aufgabe 23a:
Zwei Biegebalken 1 und 2 sind wie in der Skizze gezeigt gelagert und durch einen Stab 3
vorspanmrngsfrei miteinander verbunden. Dann greift am Balken 2 bei C die Kraft F an.
Gegebenz El
F
:107N/m2; EA:4 . 107N; lr : l,2m;
-
2000N
Gesucht: Stabkraft und Absenkung des Punktes C
l-
11
lz
: l,6m;
ls
:
Q,bm;
Aufgabe 23b:
Ein vorspannungsfreier Biegebalken ist bei .,4, fest eingespa^nnt und bei
lager gestützt. Au seinem freien Ende greift eine Kraft P an.
Gegeben: E -- 2,1 .107N/cm2;
P:2000N
Gesucht: a) Auflagerkraft B
b) Durchbiegung uc:
I
h
I
-J
I
I
I
l--l
Querschnltt
(vergrößert)
B durch ein Gleit-
ü:3cm; lr:6cm; l:80cm; c:50cm;
Aufgabe 24a:
Ein BITRItTäger wird auf Zug belastet und um
Gegeben:E:2,1 .10-7N/" ri
a?
erwärmt.
d:2cm; c:3cm; I:2rn;
LT:80'C
a:12.106f"C;
Gesucht: a) Längenänderung
b) max. Normalspannung
b) max. Schubspannung
3oau
Zoo
lZ
Zoalz
Soop
Z
Oa4z
L
Ein TROISCINQTTäger wird wie in der Skizze angegeben belastet und um A? erwd^rmt.
Gegeben: nüüs
Gesucht: ja,nüüs
Dynarnik
Aufgabe 25a:
Ein Fahrzeug hat in der skizzierten Position 1 die Geschwindigkeit u1. Es wird dann mit
der Beschleunigung @1(s) bis zur Position 2 bewegt; dann erkennt der trbhrer den Abgrund
und verzögert das Fahrzeug, nachdem dieses eine Schrecksekunde lang mit konstantJ Geschwindigkeit dahinrollte, mit konsta^nter Beschleunigung a3 bis zum Stillstand unmittelbar
am Abgrund. Hierbei löst sich das Sur{brett vom Wagen und fällt aus der Lage 4 in die
Schlucht. Der Fahrer hört den Aufprall nach 2,b Sekunden.
Gegebeni ü1 :30km/h; or(")
:
oo(1
- s/300m);
Schallgeschwindigkeit o".tr
:
340m/s
Gesucht: 1) für ao :3m/s2 und 6m/s2
a) dt*t*
b) u2,t2
c) as,ta
2) Tiefe der Schlucht
I
t2
7///////////////////////////////m'/////
Ullrnl lr, t'
mt
ntr
'/t7///////////t
///l
I
I
Aufgabe 25b:
Auf einer horizontalen Ebene ffürt ein Wagen 1 mit konstanter Geschwindigkeit u1. Wenn
der Wagen den Ort A erreicht hat, wird ein Stein 2 aus der Höhe h über dem Ort B mit
einer Anfangsgeschwindigkeit uz : 0 losgelassen.
Gegebeni
u1
:72km/h; I :
120m
Gesucht: Wie groß muß lz gewählt werden, damit der Stein in der Mitte des Wagens
auftrifft?
+'
B
Aufgabe 26a:
Eine Seiltrommel beschleunigt ein Gewicht aus dem Stillstand (gezeichnete Lage) mit konstanter Beschleunigrrg ao :2rn/s2
Gegeben:
r:
100cm
Gesucht: a) u(t); s(t)
b) ä(t); ,i(t); o(t)
c) Lage, Geschwindigkeit und Beschleunigung der Punkte Ä und B naü,2
Sekunden
'l
Aufgabe 26b:
Eine Seiltrommel mit konstanter Winkelbeschleunigmg ö6 beschleunigt ein Gewicht aus
dem Stillstand (gezeichnete Lage)
Gegebent r
:50cm;
äs -- 3f s2
Gesucht: Lage, Geschwindigkeit und Besctrleunigung der Punkte A und B nach
Sekunden
S,V,a
I
I
I
tr:4
Aufgabe 27a:
Ein Flugzeug fliegt einen kreisförmigen Kurs über Grund. Die Eigengeschwindigkeit beträgt up : t5Okm/h. Die Windgeschwindigkeit ist u- : bOkm/h.
Gesucht: Absolute Geschwindigkeit des Flugzeuges
in den Punkten lr2r. .. ,I2
vw
(:
Geschwindigkeit über Grund)
Aufgabe 27b:
Ein Boot mit der Eigengeschwindigkeit up überquert einen Fluß mit der Strömungsgeschwindigkeit uw längs der Strecke AC
Gegebent n6
:6km/h;
uw
:3km/h;
ö
Gesucht: a) erforderlicher Vorhaltewinkel a
b) Fahrzeit t
:
200m;
0
:20"
Aufgabe 28a:
Ein Rotor besteht aus einer Stange 2, die in der skizzierten Lage die Winkelgeschwindigkeit
ä und die Winkelbeschleunigotg ä hat, und zwei gleichen punktförmigen Massen, die durch
Seilkräfte ^9 mit der Relativgeschwindigkeit u,.1 reibungsfrei zum Drehpunkt des Rotors
gezogen werden.
Gegeben:
m': 2kg; r : 0,3m;
ä
: 30r/s;
ä
: l0rfsz;
urel
: 2m,fs;,9 :
120N
Gesucht: In der skizzierten Lage
a) absolute Geschwindigkeit und absolute Beschleunigung der Massenpunkte
b) Kraft von der Stange auf die Massenpunkte
Aufgabe 28b:
Ein Massenpunkt 1 gleitet reibungsfrei auf einer Stange 2, die bei Ä drehbar gelagert ist.
Die Stange hat in der skizzierten Lage die Winkelgeschwindigkeit d und die Winkelbeschleunigung ö, die Masse 1 gleitet mit der Relativgeschwindigkeit u,4.
Gegebeni rn
:10kg; r :0,5m;
ä
: 10/s;
ö
: 50/s2; urel :
Gesucht: In der skizzierten Lage
a) absolute Geschwindigkeit und absolute Beschleunigung
b) Kraft von der Stange auf die Masse
\u,
\./
''{
5m/s
Aufgabe 29a:
Zwei Massenpunkte rn1 und rl2 werden von einem (masselosen) Balken, der sich um A
drehen lcann, gehalten. Zur Zeit t : 0 greift an dem in der skizzierten Lage in Ruhe
befindlichen System die Kraft F an.
Gegebeni
rrr,1
:30kg; Trtr2-10kg; I : 1m; F :
Gesucht: Unmittelbar nach dem Angreifen der Kraft
1200N
.F
a) Beschleunigungen @1 und a2 der Massen rn1 u\d m2
b) Kräfte von den Massen auf den Balken
c) Auflagerreaktionen bei A
m2
It
Aufgabe 29b:
Zwei Massen 1 und 2 werden durch drei gleiche (gewichtslose) Stäbe 3, 4 und 5 gehalten.
In der gezeichneten Lage ist die Winkelgeschwindigkeit o des Systems bekannt.
Gegeben: a
:lls;
rrr,1
:20kg;
rn2
:10kg;
I : 0,5m
Gesucht: In der skizzierten Lage
a) Stabkräfte 53,.9a und Ss
b) Winkelbeschleunigung ö.
['
Aufgabe
3Oa:
Die Stange 1 ist bei A drehbar gelagert und hält einen Massenpunkt 2. Bei B ist ein
Seilzug befestigt, der eine Masse 3 führt. In der skizzierten Lage hat die Stange die
Winkelgeschwindigkeit ä.
Gegebent
rrr,2
:45kg;
Trts
:12kg;
I :3r2m; a :
0,8m; ä :
0,6s-1
Gesucht: In der skizzierten Lage
a) Seilkraft
b) Auflagerreaktionen bei A
Anmerkung: Alle Elemente außer 2 und
3 sind als masselos anzusehen.
Aufgabe
3Ob:
Ein Massenpunkt wird von einem (masselosen) Balken, der sich um A dreht, gehalten. In
der gezeichneten Lage ist die Winkelgeschwindigkeit ä des Balkens bekannt.
Gegeben: rn :10kg; a :
lm; ä:
4ls
Gesucht: In der gezeichneten Lage
a) Winkelbeschleunigung ö
b) Kraft von der Masse auf den Balken
c) Auflagerreaktionen bei Ä
'j
Aufgabe 31a:
Ein Massenpunkt ist an einem (masselosen) Faden befestigt und bewegt sich auf einer
reibungsfreien Platte. In der gezeichneten Lage r : r0 hat die Masse die Geschwindigkeit
ds. Der Faden wird dann langsam von der Kraft F durch das Loch A gezogen.
Gegeben: rs
: 16'
uo
: 10m/s; rn: lkg
Gesucht: a) u(r), F(r)
b) kinetische Energie der Masse bei r: rs und
c) Arbeit der Kraft .F von 16 bis 11
r --rr:rol2
Aufgabe 31b:
Die beiden Massen 1 und 2 sind durch ein Seil untereinander verbunden. An der Masse 1,
die auf dem Fundament gleitet (U"1, greift die konstante Kraft K an. In der skizzierten
Lage hat die Masse 2 die Geschwindigkeit u6.
Gegebenz rrll
:20kg; mz:8kg; Fc :0,2i c : 30"; K: 140Ni
uo
:2rnls
Gesucht: a) Seilkraft
b) Geschwindigkeit der Masse 1, wenn sie einen Weg s : 0,8m zurückgelegt hat
Aufgabe 32a:
Eine einstufige Rakete bewege sich beschleunigt, wobei kontinuierlich Masse mit der relativeo Austrittsgeschwindigkeit or.1 ausgestoßen wird. Der Massendurchsat z fu sei zeitlich
konstant.
Gegeben!
oret
:5700m/s; uE:20000m/s
(25000 m/s)
Gesucht: Wie groß muß das Verhältnis von Anfangsmasse rno (bei der Geschwindigkeit
u :0) zur Masse rn6 der ausgebrannten Rakete sein, damit eine Endgeschwindigkeit oEr erreicht wird, wenn keine äußeren Kräifte wirken?
Aufgabe 32b:
Eine Rakete steige im Schwerefeld der Erde senkrecht nach oben, wobei der Treibstoff in
der Zeit At verbraucht wird.
Gegeben,
H :2,,9; At : 2min;
urel
:
2000m/s
Gesucht: Ermitteln Sie unter Vernachlässigung des Luftwiderstandes und der Anderung
von I und unter der Annahme eines konstanten Massendurchsatzes mit der Geschwindigkeit u..1 die Geschwindigkeit und die Höhe der Rakete nach Bremsschluß, sowie die maximal erreichbare Höhe.
l-
Aufgabe 33a:
Auf einem sich mit der Geschwindigkeit o6 reibungsfrei bewegenden Wagen der Masse rn6z
befinden sich rz Personen der Masse rn. Diese springen mit der Relativgeschwindigkeit ur"1
zum Fahrzeug in die negative Fahrtrichtung von diesem ab. Die Wagenräder betrachten
wir als masselos.
Gegeben,
ry:10; n:3
Gesucht: Die Geschwindigkeit u,, des Wagens, wenn alle Personen
a) auf einmal abspringen
b) nacheinander abspringen
nm
///t///////////////1//////////////ffi
Aufgabe 33b:
Auf einem Verschiebebahnhof stoßen n Güterwagen elastisch mit der Geschwindigkeit us
auf eine Reihe ungekoppelt aneinander stehender Güterwagen. Alle Güterwagen haben die
gleiche Masse rn.
Gesucht: a) Anzahl n' der Güterwagen, die am anderen Ende der Reihe durch den Stoß
in Bewegung versetzt werden
b) Welche Geschwindigkeit u' haben diese n' Güterwagen?
.n
Aufgabe 34a:
Zwei Scheiben 1 und 2 sind untereinander und mit dem Fundament gelenkig verbunden.
In der gezeichneten Lage sind die Winkelgeschwindigkeiten ä1 und äz sowie die Winkelbeschleunigung ä1 und ö2 der Scheiben 1 und 2 bekannt.
Gegeben:
l: 0,5m; r :0,3m; är :7ls;
az
:b/s;
är
: 40/s2; äz :20/s2
Gesucht: a) Geschwindigkeiten rip und d6 der punkte B und C
b) Beschleunigungen dp und äo der Punkte B und C
Aufgabe 34b:
Gegeben ist ein Getriebe, bestehend aus der Stange 1 und der Scheibe 2. In der gezeichneten Lage hat die Stange 1 die Winkelgeschwindigkeit d1 und die Winkelbeschleunigung
är. Die Scheibe 2 rutscht bei D auf einer Führung.
Gegeben:
J
: 1m; ät :4ls;
är :201s2
Gesucht: In der skizzierten Lage
a) Geschwindigkeit dn des Punktes E
b) Beschleunigung d6r des Punktes C
Aufgabe 35a:
In der gezeichneten Lage or :60" sind die Winkelgeschwindigkeit d1 und die Winkelbeschleunigung ör der Kurbel 1 einer Kurbelschwinge bekannt.
Gegeben:
a:20cm; /: 110cm; b:50cm; ät :721s; är:
maßstäbliche Skizze M : 1:10
100/s2
Gesucht: In der skizzierten Lage
a) Geschwindigkeitszustand und Beschleunigungszustand des Abtriebs durch
Angabe von u6, ds, äs, äs
b) d2, ä2
Aufgabe 35b:
In der skizzierten Lage a1 : 60" sind die Winkelgeschwindigkeit d1 und die Winkelbeschleunigung ör der Excenterscheibe L bekannt.
:0,32m; I : 0,9m; är :2ls;
maßstäbliche Skizze M : 1:10
Gegebeni r
är :201s2
Gesucht: In der skizzierten Lage
a) Geschwindigkeit und Beschleunigung des Punktes L
b) Geschwindigkeitszustand und Beschleunigungszustand der Koppel 2 durch
Angabe von d2, ä2 und ön,de
Aufgabe 36a:
In der skizzierten Lage wird der Balken 3 von den beiden Seilzügen 1 und 2, die die Massen
rn1 und rn2 halten, bewegt. Die Geschwindigkeiten der Massen sind o1 und u2.
Gegebenz
trll:10kg; rrtr2:15kg;
rne
:5kgi l:0,8m;
ur
: 1m/si uz:4mls
Gesucht: In der skizzierten Lage
a) kinetische Energie des Systems
b) ein Gleichungssystem zur Ermittlung der Seilkrdfte
I'
Aufgabe 36b:
Der schwere Balken 1. ist bei A drehbar gelagert. Er ist über einen Seilzug mit dem Klotz
2 verbunden, an dem die Kraft K angreift. In der skizzierten Lage hat der Klotz die
Geschwindigkeit uz : Srnls.
Gegebent
Tn1
--
20kg; rrtrz:40kg; I -
0,8m;
K
:
200N;
Gesucht: In der skizzierten Lage
a) Seilkraft
b) innere Kraft im Schnitt B-B
I,
r-ä+ä-1
Aufgabe 37a:
Die schwere Scheibe 1 ist mit den Stäben 2 und 3 verbunden. Das System dreht sich aus
der Ruhelage I in die Lage 2, wobei sich die in der Lage 1 ungespannte Feder ausdehnt.
Gegeben:
rn:10kg;
a:
0,6m; b: al2;
maßstäbliche Skizze M : 1:10
c
:
Gesucht: In der Lage 2
a) Winkelgeschwindi gkeit
b) Winkelbeschleunigung und Stabkrdfte
t_
I
j
150N/m;
Aufgabe 37b:
Der Balken 1 dreht sich um das Lager Ä. Das Ende B des Balkens bewegt einen Seilzug,
der eine Masse 2 häJt. In der skizzierten Lage t hat der Balken die Winkelgeschwindigkeit
ar : 4ls; am Balken greift ein konstantes Moment M :200N.m an.
Gegebeni rrtl
:12kg;
rnz
: 8kg; I :
t,2rn
Gesucht: In der gestrichelt skizzierten Lage 2
a) Winkelgeschwindigkeit des Balkens
b) Seilkra,ft
l.
Aufgabe 38a:
Das skizzierte System besteht aus der Walze 1 und einem (masselosen) Seil B, das (reibungsfrei) über eine Rolle geführt ist und eine Masse 2 hält. An der M*"" 2 greift eine
Kraft -F a^n. Die walze rollt aus der Ruhelage I in die Lage II.
Gegeben: schwerpunktsbeschleunigung der walze
a:8m/s2i rnr:
frt2:10kg; r:20cm; s:100cm; a:30"
20kg;
Gesucht: In der Lage II
a) Geschwindigkeit des Schwerpunktes von 1
b) Beschleunigung des Punktes von 1, der den Boden berührt
c) kinetische Energie des Systems
d) Auflagerreaktion
e) erforderliche Kraft F
f) Impuls der Kraft .F von I bis II
g) Leistung der Kraft -F bei II
I
sl
Aufgabe 38b:
Das skizzierte System besteht aus dem Klotz 1 und der Walze 2, die über eine
(masselose)
Stange 3 verbunden sind. An der Walze 2 greift eine Kraft -F an. Das System bewegt
sich
aus der Ruhelage I in die Lage II, wobei der Klotz rutscht und die Walze rollt.
Gegeben: Gleitreibungszahl pG :0,2;
r:0,3m; l-3r;
b:2r;
rrll
:40kg;
rn2
:30kg;
s
:
3m;
cr:80"
Gesucht: a) Kraft -F so, daß der Schwerpunkt der Walze 2 die konstante Beschleunigrrrrg
:6m/s2
In der Lage II
az
erhält
b) Geschwindigkeit des Schwerpunktes von 2
c) Auflagerreaktionen für 1
d) Arbeit und Impuls der Kraft -t'von I nach II
e) Arbeiten der Reibkräfte
f) Leistung der Kraft F
(r
'j
Aufgabe 39a:
Aus der skizzierten Ruhelage gleitet der Balken 1 auf einem reibungsfreien Vorsprung .4
und dreht dabei eine Scheibe 2, die bei C gebremst wird. Die Anpreßkraft der Bremse ist
.F, die Gleitreibungszahl ist p - 0,2.
Gegebenz rrly :20kg; rrl2 :
10kg; r : 0,2m; ö - 0,3m;
Gesucht: wenn der Balken 1 den Weg b zurückgelegt hat
a) Geschwindigkeit und Besctrleunigung des Balkens
b) kinetische Energie der Scheibe 2
c) Arbeit der Bremskraft
d) Arbeit, die der Balken 1 an der Scheibe 2 verrichtet
t,
,t
Ij.}t =0
-F
:
100N
Aufgabe 39b:
Eine Walze 1 und eine Seiltrommel2 sind durch einen Seilzug verbunden. Der Seilzug hält
über eine Rolle eine Masse 3. Das System wird aus der gezeichneten Ruhelage I losgelassen.
Die Umlenkrollen und das Seil sind als masselos anzusehen.
Gegeben: rn1 -
5kg;
rnz
: 8kg;
rrls
:20kg; r :
Gesucht: nadr einer Umdrehung der Walze (Lage II)
a) Seilkraft
b) Geschwindigkeit der Masse 3
o
4///t
/
0,,2m
Aufgabe
4Oa:
Ein Massenpunkt wird von drei Schraubenfedern 1,2,3 und einer Blattfeder 4 gehalten.
In der skizzierten Lage sind alle Federn ungespannt und der Massenpunkt bewegisich mit
der Geschwindigkeit us nach unten. Die Massen der Federn sind zu vernachläsrlg"rr.
Gegeben: m : 2kg; cr : 500N/cm; cz : 300N/cm;
EI /13 : 185,2N/cm; uo :2m/s
ce
:
1000N/cm;
Gesucht: a) Federkonstante des Federsystems
b) Differentialgleichung der Bewegung ("kleine schwing'ngen")
c) Kreisfrequenz, Frequenz, Schwingungsdauer, Amplitude und Phasenwinkel
der Schwingung
Aufgabe
4Ob:
Ein Massenpunkt wird von drei Schraubenfedern !,2, 3 und einer Blattfeder 4 gehalten.
In der skizzierten Lage sind alle Federn ungespannt und der Massenpunkt bewegt sich mit
der Geschwindigkeit os nach unten. Die Massen der Federn sind zu vernachlässigen.
Gegeben:
m:2kg; cr : 500N/cm; cz : 300N/cm;
EI lI3 : 185,2N/cm; uo :2m/s
cs
:
1000N/cm;
Gesucht: a) Federkonstante des Federsystems
b) Differentialgleichung der Bewegung ( "kleine Schwingungen" )
c) Kreisfrequenz, Flequenz, Schwingungsdauer, Amplitude und Phasenwinkel
der Schwingung
Aufgabe 41a:
Das skizzierte Pendel besteht aus der Kreisscheibe 1 und dem schlanken Balken 2, die bei
A miteinander verschweißt sind. Das Pendel ist im Punkt B gelagert und führt um die
skizzierte statische Ruhelage Schwingungen mit kleiner Amplitude aus.
Gegeben: m2 - 4m11 I :4r:
30cm
Gesucht: a) Differentialgleichung der Bewegung
b) eine obere Schranke für o
l
ls
I
T
a
J-
Aufgabe 41b:
Ein schlanker Stab ist bei Ä drehbar gelagert und wird durch eine Drehfeder mit der
Federsteifigkeit c gehalten.
Gegeben:
l:0,4m; n',,: lkg
Gesucht: a) Wie groß muß c sein, damit der Stab kleine Schwingungen um die skizzierte
Ruhelage mit der Kreisfrequenz 4fs ausführt?
b) eine untere Schranke für c, wenn das Gleichgewicht in der skizzierten Lage
stabil sein soll
j'
Aufgabe 42a:
Eine Kreisscheibe ist mit einer Blattfeder verbunden, deren a''deres Ende in einem Gleitstein fest eingespannt ist. Dieser wird mit s : s0 sin art horizontal bewegt. Die Kreisscheiberollt auf einer Ebene,
Gegeben: I :
0,7m; r :0,3m;
rn
: 0,5kg; EI :
2. 105N.cm2;
.eo
:
0,5cm
Gesucht: a) Differentialgleichung der Bewegung des Mittelpunktes der Kreisscheibe
b) Kreisfrequenz der Erregung, wenn die Amplitude der Bewegung der Kreisscheibe halb so groß werden soll wie die Amplitude der Erregung
.. ..- /
.z .z
Aufgabe 42b:
Ein dünner Balken ist bei A drehbar gelagert und wird von einer Drehfeder gehalten.
Das freie Ende einer mit dem Balken verbundenen Feder wird horizontal bewegt. In der
skizzierten Lage sind beide Federn ungespannt.
Gegeben:
m: 4kg; I : 1m;
d
: 40N.m; c:60N/m;
s0
:
2mm
Gesucht: Erregerkreisfrequenz so, da3 die Amplitude der Drehbewegung
des Balkens 0,01
beträgt
= xocostot
4
Vier Klausuren
T/T
l.Aufgabe: Der Balken 1 wird durch sein Eigengewicht G1 und durch
die Kraft F so gegen die Seiltrommel 2 gedrückt, daß diese das
Gewicht G3 durch die Reibung bei C halten kann.
Gegeben: G 1 =400N; G3 =1200N;
Haftreibungszahl [r=0,3
Gesucht:
a)
b)
a=0,6ffii
b=0,4m i
Wie groß muß die Kraft F mindestens sein?
Schnittlasten als Funktion von x für F=1200N.
r7=2r 1i
L/2
2. Aulgabe: Der Biegebalken
1 (E'la) wird von zwei gleichen Stäben 2und 3 (E.A)
und den Auflagern A und B vorspannungsfrei gehalten. Dann wird am Balken das
Gewicht G angehängt.
Gegeben: E't"=1O8Ncm2; E-A=l05N; G=500N;
l=1
,2m; a=ll2
Formel: f=Kl3/48E.la
Gesucht: a) Stabkräfte (für die statische Ruhelage)
b) Federsteifigkeit des Systems
c) Eigenkreisfrequenz lür kleine Schwingungen.
Ir
,-
l(
|
Ll3
3-Aufgabe: Eine Kreisscheibe (Mass€ ffi, alle anderen Teile sind als masselos
anzusehen) wird über einen Seilzug aus der Ruhelage 1 über eine schiefe Ebene
gezogen. Die Kreissscheibe rollt, die Seiltrommel wird durch ein konstantes Moment
ängetrieben.
Gegeben: m=6kgi r=0,2m, ä=0,1rn; s=2m; a=30o; M=1ONm
Gesucht: a) Auflagerreaktion in der Lage 1
b) Winkelgeschwindikeit der Kreisscheibe in der Lage 2.
Ll4
4.Aufgabe
:
Fragenteil; richtige Antworten ankreuzen.
a) Die Lagerung des Systems
//
b)
c)
ist
Bei gegebener Normalkraft
liefert die Gleitreibungszahl
d) Fü
ist
A1
die maximale Schubspannung
ZOa ,u/r,rnrL
e) Bei gegebenen r,v und E gilt für y
) Das Flächenträgheitsmoment
zur
Berechnung der Biegespannung ist
Die CORlOllSbeschleunigung ist
€S
e^
h)
i
)
stab il
c
die Reibkraft'R
den Betrag von R
eine obere Grenze für
a
b
c
kleiner
a
b
b
g rö
unverändert
ßer
c
0
a
150N/mm2
50 N/mm2
b
öen skizzierten Spannungszustand
/aatu/-n,z
g)
a
Die Stabkraft 1 wird mit
wachsender Querschnittsfläche
f
statisch bestimmt
statisch unbestimmt
ffi
c
tE
2r(r+v)lE
rEl2(1+v)
a
b
c
np4-a4yrcz
a
r ( D-d)4lo+
r1o4 -a4y ta+
b
c
o)
vrelcten
a
2v," 1ä,d1
2vr"1ü-n
b
c
&.
Rotationsenergie
Der Drall ist
die
das
das
Die Arbeit einer Kraft ist
ihr Zeitintegral
a
ihr vektorielles Wegintegral b
lmpulsmoment
Drehmoment
ihr skalares
Wegintegral
a
b
c
c
2/L
l.Aufgabe F91E: Die schwere Scheibe 1 ist bei A gelagert und stützt
sich bei B reibungsfrei gegen den Träger 2, der bei C gelagert ist. Mit
dem Träger gelenkig verbunden ist der Balken 3, der sich bei D mit
Reibung gegen das Fundament stützt. Das System befindet sich in
Ruhe.
Gegeben: maßst. Skizze M=1
'gewichtslos"
:10;
G1
=
300N, alle anderen Teile
Gesucht: a) erforderliche Haftreibungszahl bei D
b) maximales Biegemoment im Balken 2
c) Auflagerreaktion bei C.
/////'
212
2.Aufgabe: Der Balken 1 (El) ist bei A fest eingespannt und bei C mit
zwei Seilen 2 und 3 (EA) vorspannungsfrei verbunden. Das Seil 3 hält
die Masse m.
Gegeben: ll
Gesucht:
=1
a)
,2m;
l2=1
,4m; lg=0,6m; m=14kgi El=105Nm2; EA=2'1 06N
Absenkung
der Masse gegenüber der unbelasteten
Lage
b) Eigenkreisfrequenz der Vertikalschwingung der Masse.
2/3
3.Aufgabe: Die Walze 1 rollt und der Quader 2 rutscht auf einer
schiefen Ebene. Die Watze ist durch eine Feder mit dem Fundament,
durch eine Stange mit dem Quader verbunden. Der Quader wird von
einem Seilzug gezogen, der die Masse 3 hält.ln der skizzierten Lage ist
die Feder ungespannt, die Masse 3 hat dort die Geschwindigkeit v.
Gqgeben: m 1 =4kgl m2=6kg; mg=gkg; r=0,2ffi; v=3m/s; c=200N/m;
FG=o'2
Gesucht: a) Kraft in der Stange in der skizzierten Lage
b) Eine Gleichung zur Ermittlung der maximalen Ausdehnung
der Feder.
I'
2/4
4.Aufgabe F91: Fragenteil, richtige Antworten ankreuzen
a) Die Lagerung des Systems ist
statisch unbestimmt
statisch bestimmt
a
verschiebbar
c
gleich
kleiner
größer
a
c
G I/B
a
0
3G
b
b
t
b) Die Haftreibungszahl ist im Vergleich
zur Gleitreibungszahl
c) Das Biegemoment bei C ist
F.6/27 /V
Lr
d) Die maximale' Schubspannung ist
---+ - ,/ 3@'{//'r"tz
4LWISral/a,;
-,
e)
Die maximale Druckspannung ist
-rfkl
h) Die CORlOLlSkraft
ist
i) Die Leistung einer Kraft ist
heißt
a
b
c
6M/d-4 F)tndz
(8Md-6F) tndz
(32M/d+4 F)lnd2
a
b
c
bis
zum Stillstand; die Beschleunigung"ist ca.
g) Das Wegintegral einer Kraft
c
500N/mm2
250N/mm2
1 000 N/mm2
(1
v-
f) Ein PKW bremst in 20s von15Okm/h
l/4
b
4mls2
2mls2
6 m/s
lmpu ls
a
b
c
Leistung
Arbe it
a
b
c
2mvdr"1
a
2mäv r"1
b
2mrv r"1
c
Fds/dt
Fv2lz
a
FZv
c
b
3/r
l.Aufgabe: Die Scheibe 1 ist bei A gelagert und stützt sich bei B gegen das
Fundament (Haftreibung). Die Scheibe wird durch einen Seilzug belastet, der ein
Gewicht G2 hält. Das Gewicht der Rolle 3 und des Seils 4 ist zu vernachlässigen.
Gegeben: maßstäbliche Skizze M=1:'10; G1=300N; G2=600N
Gesucht: a) Auflagerreaktionen bei A und B
b) erfordertliche Haftreibungszahl bei B
c) lnnere Kraft im Schnitt E-E bezogen auf den Punkt S.
Ip
3/2
2.Aufgabe F91E: Die zwei gleichen Biegebalken 1 und 2 sind bei A
und
B fest eingespannt und in ihrer Mitte durch den stab 3
vorspannungsfrei verbunden. Das Tragwerk wird durch das Gewicht G5
belastet, das von dem Stab 4 gehalten wird.
Gegeben:
11
E
=120cmi 13=60cm; 14=30cm; a=4crTl; b=3cm; d=0,1cm;
1
=
E3=f 4=E=2' 107N/cm2i G5=200 N
Gesucht: a) Absenkung des Gewichtes
b) maximales Biegemoment im Balken 2
c) Maximale Zugspannung im Balken
2 (falls b) nicht
beantwortet mit Mbma, = 240N.m rechnen).
3/3
3.Aufgabe F91E: Aus der skizzierten Ruhelage heraus wird ein
Rotor,
der aus den Kreissscheiben 1 und den gleichen, schlanken Balken 2 und
3 zusammengeschweißt ist, durch das Gewicht G5 und die Feder 6, die
in der Ruhelage ungespannt ist, gedreht.
Gegeben:
J
t R=0,8kg m2; m2=2kg; GS=50Ni c=140N/m; l=0,4m;
R=0,3m; r=0,1m
Gesucht: a) nach einer halben Umdrehung des Rotors: Geschwindigkeit
des Gewichtes 5, Seilkraft 54
b) . Eigenkreisfrequenz für kleine Schwingungen um die
statische Ruhelage
3/4
4.Aufgabe: Fragenteil, richtige Antworten ankreuzen
a) Die Lagerung des Systems ist
b) Die
n*
Gleitreibungszahl
zur Haftreibungszahl
ist
im Vergleich
c) Das maximale Biegemomen t ist
Lr
7z'z
d) Die maximale Zugspannung ist
-t
f loo'u/n-,2
J,U
Cie) Die Biegespannung ist
Ein PKW beschleunigt in ca. 15s von 0 auf
100km/h; die Beschleunigung ist ca.
s) Das Zeitintegral einer Kraft heißt
statisch bestimmt
statisch unbestimmt
indifferent
a
gleich
kleiner
größer
a
c
G
l/8
G,t4
3G l/4
a
b
c
0
a
b
c
b
c
b
50N/mm2
100N/mm2
6'Ml/a3
6M/a3
a
12Mla
c
9m/s2
Zmts2
6 rn/s
a
lmpuls
a
b
c
b
b
c
L'eistung
Arbe it
:
h)
Die Fliehkraft ist
i) Die Arbeit eines konstanten
Momentes ist
fnra
a
mro,2
b
2mrvr"1
c
Mv
Mv2t'2
Ma
*
a
b
c
4/r
l.Aufgabe H91E: Zwei Balken 1 und 2 sind untereinander
gelenkig
verbunden und werden bei A durch ein festes Auflager, bei B und C von
zwei stäben gehalten. Die Konstruktion hält das Gewicht G.
Gegeben: maBst. Skizze M=1:10; G1=G2=300N; G=800N; atte anderen
Teile 'gewichtslos"
Gesucht: a) Stabkräfte (Zug oder Druck angeben)
b) lnnere Kraft im Schnitt D-D.
4/2
2.Aulgabe H91E: Der skizzierte lange Kessel wird
durch einen
inneren Überdurck p=2N/mm2 belastet.
Gegeben: d=0.8m; s=smm; E=2'105N/mm2l v=0,3
Gesucht: a) maximale Schubspannung bei A (ebenes Problem)
b) Dehnung der Richtung 1 bei A
Anmerkung:
Kesselformel o1=2o"=p'dl2s.
4/3
3.Aulgabe H91E: Die Seiltrommel 1 ist über ein Seil mit der
rollenden Walze 2 verbunden. ln der skizzierten Lage "0" ist die
Winkelgeschwindigkeit der Trommel, die durch ein konstantes
Drehmoment M6=2N'm angetrieben wird, ,it O.
Gegeben: J1=0,08kg'm2; rh2--2kg; 11=0,2m; r2=0,3m; &t
g=r/t
Gesucht: a) Winkelgeschwindigkeit der Walze &ZO in der Lage '0"
b) Leistung des Drehmomentes in der Lage "0"
c) Seilkraft
d)
Winkelgeschwindigkeit der Watze
drehung der Trommel.
&Zl
nach einer Um-
4/4
4.Aufgabe H91E: Fragenteil, richtige Antworten ankreuzen
a)
Die Auflagerreaktion beiA ist
6= *f,ap
b)
Das maximale Biegemoment ist
tr
Die Gleichgewichtsbedingungen
XM4=Q; IMg=Q; XM6=Q sind hier
d) Die maximale Schubspannung
ist
240N
a
320N
b
4BON
c
Fy8
a
Flt4
b
3FV4
c
notwendig
hinreichend
notw. und hinreichend
a
100N/mm2
e)
Die maximale Biegespannung ist
200N/mm2
4Flta3
a
ry"3
b
1ZFlta3
c
16s
Bs
a
b
c
mlr&2
a
mr&2
b
mvr";/r
c
Fds/dt
FvZ t2
a
F2v
c
15,7Nm2/s
a
1,6kg m2ls
b
3,2Nm2/s
c
ä
q.W
a_
F
c
a
b
c
50N/mm2
4aolV*^z
b
f) Ein PKW bremst von1S0km/h bis 0
tn11
s=g/2; die Bremszeit ist ca.
4s
g) Die Fliehkraft ist
h) Die Leistung einer Kraft ist
i)
Der Drall bezüglich A ist
otL^
O'ry
Ir
b