Die Brüche - EDUmobile

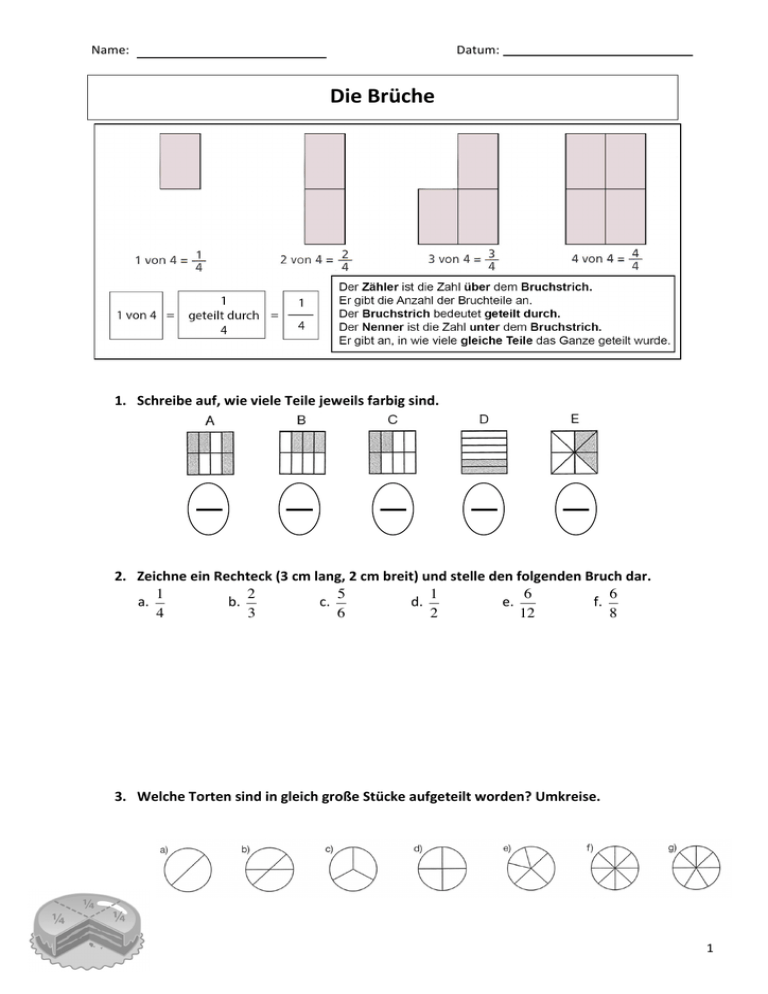
Name: Datum: Die Brüche 1. Schreibe auf, wie viele Teile jeweils farbig sind. 2. Zeichne ein Rechteck (3 cm lang, 2 cm breit) und stelle den folgenden Bruch dar. 1
2
5
1
6
6
a. b. c. d. e. f. 4
3
6
2
12
8 3. Welche Torten sind in gleich große Stücke aufgeteilt worden? Umkreise. 1 Name: Datum: 4. a. Ich teile durch 4 und erhalte: b. Ich teile durch 8 und erhalte: 4
4
d. Ich teile durch 32 und erhalte: e. Ich teile durch ...... und erhalte: 100
100
f. Ich teile durch ...... und erhalte: 40
c. Ich teile durch ...... und erhalte: 40
5. Schreibe die passenden Bruchzahlen auf. Zeichne den Bruchstrich mit deinem Lineal! a) ___ b) c) d) e) g) h) i) j) k) f) Die Brucharten Dezimalbruch: 1 40 352
;
;
;... 10 100 1000
6 12 100
;
;...
3 4 25
Scheinbruch: ;
2 Name: Datum: 6. Benenne die Brüche mit: echter Bruch, unechter Bruch, gemischter Bruch, Zehnerbruch oder Scheinbruch 3
6
5
4
3
a. b. c. 4 d. e. 2 10
5
12
2
7
_________ f. 1
53
_________ _________ g. 93
94
_________ _________ _________ _________ h. 69
23
i. 54
100
j. 42
30
_________ _________ _________ 7. Nenne 5 Brüche, bei denen ... a. der Zähler kleiner ist als der Nenner (Z < N): ________________________ b. der Zähler größer ist als der Nenner (Z > N): ________________________ c. der Zähler gleich ist zu 1 (Z = 1): ________________________ Die gemischten Zahlen Bei einem echten Bruch gilt: Bei einem unechten Bruch gilt: ___________________ ___________________ Einen unechten Bruch kann man in eine gemischte Zahl umwandeln. Eine gemischte Zahl besteht mindestens aus einem Ganzen und einem Bruchteil. 7
=
4 3 Name: Datum: 8. Schreibe neben den Bruch ‚echt’ oder ‚unecht’. 5
_________ 4
2
_______ 3 _________ Färbe die angegebenen Bruchteile! 4
6
15
6 _________ 9. Verwandle in unechte Brüche. 4 Name: Datum: 10. Verwandle in gemischte Zahlen. Brüche vergleichen Wenn ich Brüche miteinander vergleiche, schaue ich zuerst nach dem Nenner: 1. Ist der Nenner gleich groß, vergleiche ich die Zähler miteinander. 2. Ist der Nenner verschieden groß, der Zähler aber gleich groß, dann gilt: Je größer der Nenner, umso kleiner die Teile! 11. Vergleiche! Setze das richtige Zeichen ein (<, >, =). 5 Name: Datum: Brüche erweitern und kürzen Beim Erweitern eines Bruches werden Zähler und Nenner mit der gleichen Zahl mal genommen. Wir nutzen beim Erweitern das kleinste gemeinsame Vielfache (kgV). Der Wert des Bruches ändert sich nicht! 12. Bestimme die erweiterten Brüche. 13. Berechne das Ergebnis. 6 Name: Datum: 14. Mit welcher Zahl wurde erweitert? Setze ein. Beim Kürzen eines Bruches werden Zähler und Nenner durch die gleiche Zahl geteilt. Wir nutzen beim Kürzen den größten gemeinsamen Teiler (ggT). Der Wert des Bruches ändert sich nicht! 15. Bestimme die gekürzten Brüche. 16. Kürze die Brüche schrittweise. 17. Kürze die Brüche durch die größtmögliche Zahl. 7 Name: Datum: 18. Kürze die Brüche so weit wie möglich. 19. Schreibe vier Brüche auf, die man nicht kürzen kann. Brüche auf der Zahlenstraße Auf dieser Zahlenstraße sind die ganzen Zahlen eingetragen. Die kleinen Striche teilen jedes Ganze in _____ Zehntel. Der dicke Strich ist genau 1 Ganzes 5 Zehntel. Als Dezimalzahl schreiben wir: _____. Als Bruch schreiben wie: _____. Wichtige Brüche und Dezimalzahlen: 1
2
1
4
ê 0,25 ê 0,5 1
5
1
8
ê 0,2 ê 0,125 1
10
1
100
ê 0,1 ê 0,01 20. Trage folgende Werte auf der Zahlenstraße ein: 1
2
6
5
a) 1 2 3 10
10
10
10
4
1
1000
ê 0,001 3
10 b) 0,5 2,0 3,7 1,9 5,4 8 Name: Datum: Schreibe diese Zahl als Bruchzahl Dezimalzahl 6 Zehntel 0 Ganze 9 Zehntel 9 Ganze 1 Zehntel 13 Ganze 31 Hundertstel 26 Ganze 142 Tausendstel 8 Tausendstel Brüche addieren 21. Zeichne die Bruchteile in das vorgegeben Rechteck ein und löse die Aufgabe. Kürze das Ergebnis, wenn möglich. a) 1
+ 3
= + 1
= 3
b) = + 6
+ 12
= 9
12
9 Name: Datum: 22. Erfinde selbst Aufgaben zur Addition der Brüche. Zeichne die Bruchteile in das Rechteck und löse die Aufgabe. = a) + b) + = c) + = d) + = e) + = 10 Name: Datum: 23. Erweitere zuerst auf den gleichen Nenner. Addiere dann die Brüche. 11