Kapitel5.6
Werbung
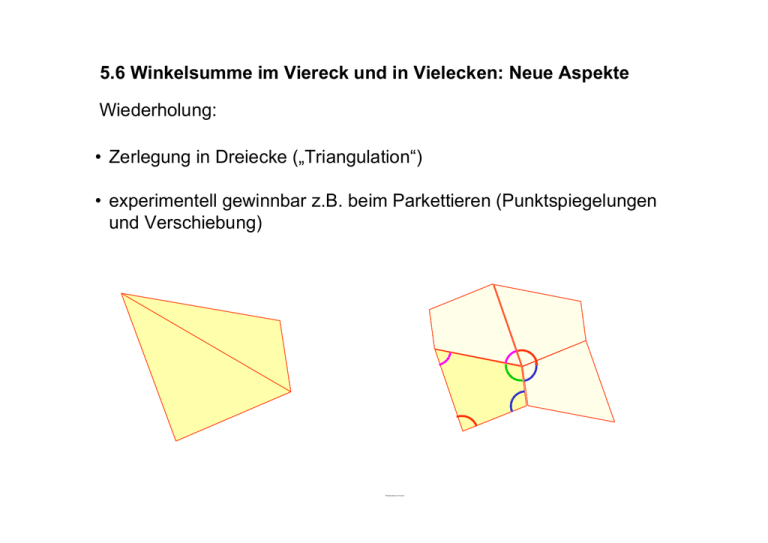
5.6 Winkelsumme im Viereck und in Vielecken: Neue Aspekte Wiederholung: • Zerlegung in Dreiecke („Triangulation“) • experimentell gewinnbar z.B. beim Parkettieren (Punktspiegelungen und Verschiebung) Winkelsumme im Viereck • Dynamischer Beweis Wozu ein weiterer Beweis? Neue Erkenntnisse? Umfassendere Sichtweise? • Man durchläuft das Viereck vom Startpunkt A einmal im Gegenuhrzeigersinn. • An jeder Ecke ändert man die Richtung um den Winkel βi. • Was kann man über die Summe der βi sagen? • Die Innenwinkel des Vierecks sind mit αi bezeichnet. • Benutzen Sie den Zusammenhang zwischen αi und βi um die Summe der αi zu bestimmen. • Übertragen Sie den Beweis auf n-Ecke. D β4 α4 A β1 α1 α3 α2 β2 β3 C B Winkelsumme im Viereck dynamisch Gilt der Winkelsummensatz auch für „überschlagene“ Vierecke? A C B • Zunächst scheint das Beispiel zu zeigen, dass der Satz nicht mehr stimmt! • Kann man ihn noch retten? • Was sind hier eigentlich die Winkel im Viereck? D A α1 α3 C α 3' α2 B α 4' α4 D • Welche Vorzeichen sollten die Winkel α3‘ und α4‘ haben? • Welche Winkelsumme ergibt sich, wenn man als Winkelsumme α1 + α2 + α3‘ + α4‘ verwendet? • Welche Winkelsumme ergibt sich, wenn man statt dessen als Winkelsumme α1 + α2 + α3 + α4 verwendet? Winkelsumme im Viereck überschlagen statisch Winkelsummensatz unter Verwendung vorzeichenbehafteter Winkel. Zunächst vernachlässigen wir Winkelorientierungen. Man sieht, dass γ1 = γ2 ist. A α1 C α2 B γ1 α 3' γ2 α 4' D Daraus folgt α1 + α2 = α3‘ + α4‘ . Werden die Winkel α3‘ und α4‘ wegen ihrer Orientierung mit negativen Werten versehen, dann erhält man als Winkelsumme 0. Winkelsumme im Viereck überschlagen statisch Betrachtung nur von positiven Winkeln, im Gegenuhrzeigersinn orientiert • Was ist die Summe der βi? A α1 α3 C α2 • Welcher Zusammenhang besteht zwischen den Winkeln αi und βi? • Was ergibt sich für die Summe der αi ? B α4 D ∑ βi = 2·360° A β1 α1 β3 C α2 β2 B D α4 β4 α3 α1 + β1 = 180° α2 + β2 = 180° α3 + β3 = 360°+180° α4 + β4 = 360°+180° ∑ (αi + βi) = 2·360° + 4·180° ∑ αi = 4·180° = 720° Winkelsumme im Viereck überschlagen dynamisch Aufgabe aus dem Schweizer Mathbu.ch, 7. Schuljahr Winkelsumme im Stern-n-Eck Mathbuch Original Fortsetzung 7-Ecke mit DynaGeo: Was kann man hier wohl über die Winkelsumme sagen? Æ Experimente Winkelsumme im Stern-n-Eck Mathbuch Experimente mit DynaGeo Æ Experimente Winkel α gegeben Æ Welcher Außenwinkel β gehört dazu? Nach wie vielen Umdrehungen k schließt sich die Figur? Wie viele Ecken n hat die Figur dann? 0 β w = 50 180 α 130 ° 50 ° Winkelsumme im Stern-n-Eck Mathbuch Weitere Bilder dazu mit Dynageo 0 β w = 72 Æ Experimente 180 α 108 ° 72 ° Winkelsumme im Stern-n-Eck Mathbuch Weitere Bilder dazu mit Dynageo 0 β 135 ° 45 ° w = 45 Æ Experimente 180 α Winkelsumme im Stern-n-Eck Mathbuch Weitere Bilder dazu mit Dynageo 0 β 136 ° 44 ° w = 44 Æ Experimente 180 α Winkelsumme im Stern-n-Eck Mathbuch n Punkte auf einem Kreis gleichmäßig verteilt. Wie kann man verschiedene regelmäßige n-Ecke erzeugen? - Jeden Punkt mit dem nächsten Nachbarn verbinden - Jeden Punkt mit dem übernächsten Nachbarn verbinden Jeden Punkt mit dem über-übernächsten Nachbarn verbinden …. Æ Experimente 2 n = 20 20 Zentrum s winkel = 360/n 18 2 Winkelsumme im Stern-n-Eck Mathbuch n = 20 20 Zentrum s winkel = 360/n 18 Experimente Æ Experimente Für welche Eckenzahl n und welche Umdrehungszahl k gibt es regelmäßige n-Sterne mit dieser Umdrehungszahl? Wie berechnet man den einzelnen Winkel aus n und k? Was ist die Winkelsumme? Winkelsumme im Stern-n-Eck Mathbuch