Lösungen

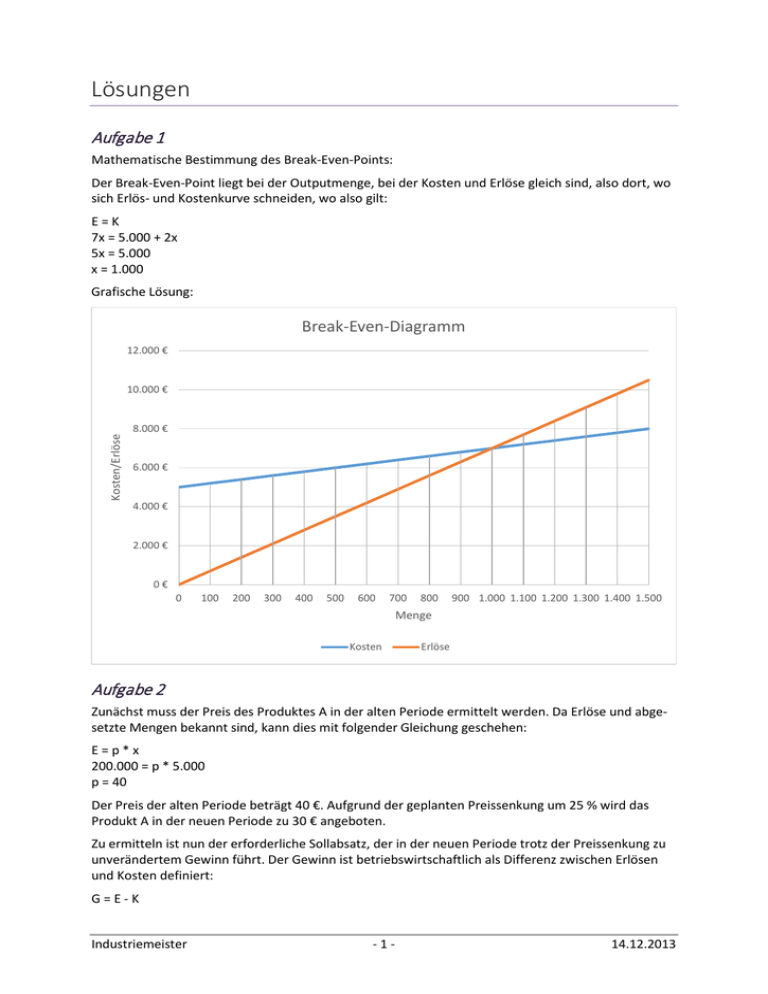
Lösungen
Aufgabe 1
Mathematische Bestimmung des Break-Even-Points:
Der Break-Even-Point liegt bei der Outputmenge, bei der Kosten und Erlöse gleich sind, also dort, wo
sich Erlös- und Kostenkurve schneiden, wo also gilt:
E=K
7x = 5.000 + 2x
5x = 5.000
x = 1.000
Grafische Lösung:
Break-Even-Diagramm
12.000 €
Kosten/Erlöse
10.000 €
8.000 €
6.000 €
4.000 €
2.000 €
0€
0
100
200
300
400
500
600
700
800
900 1.000 1.100 1.200 1.300 1.400 1.500
Menge
Kosten
Erlöse
Aufgabe 2
Zunächst muss der Preis des Produktes A in der alten Periode ermittelt werden. Da Erlöse und abgesetzte Mengen bekannt sind, kann dies mit folgender Gleichung geschehen:
E=p*x
200.000 = p * 5.000
p = 40
Der Preis der alten Periode beträgt 40 €. Aufgrund der geplanten Preissenkung um 25 % wird das
Produkt A in der neuen Periode zu 30 € angeboten.
Zu ermitteln ist nun der erforderliche Sollabsatz, der in der neuen Periode trotz der Preissenkung zu
unverändertem Gewinn führt. Der Gewinn ist betriebswirtschaftlich als Differenz zwischen Erlösen
und Kosten definiert:
G=E-K
Industriemeister
-1-
14.12.2013
Die Gleichung lässt sich nun folgendermaßen umformen:
G = p * x – (Kf + kv * x)
In dieser Gleichung gibt es zwei unbekannte Größen, nämlich x (die gesuchte Größe oder der Sollabsatz der neuen Periode) und kv. kv kann folgendermaßen ermittelt werden:
kv=
Kv 120.000
=
=24
x
5.000
Nun gibt es in der Gleichung nur noch eine Unbekannte x, die sich errechnen lässt:
40.000 = 30x - (40.000 + 24x)
40.000 = 30x - 40.000 - 24x
80.000 = 6x
x = 13.333,33 (Sollabsatz)
Bei einem Absatz von 13.333,33 Einheiten bleibt der Gewinn trotz der Preissenkung in der neuen Periode 40.000 €.
Der Sollumsatz beträgt dann:
E=p*x
E = 30 * 13.333,33
E = 400.000
Aufgabe 3
Die Sozialkosten betragen laut Aufgabenstellung 15 % der Löhne und Gehälter. Wenn die Löhne im
neuen Jahr 147.000 € betragen, so entsprechen hiervon 15 % einem Betrag von 22.050 €, die als variable Kosten zu betrachten sind, da die Löhne ebenfalls variabel sind. Die Gehälter belaufen sich in
der neuen Periode auf 63.000 €, 15 % hiervon entsprechen 9.450 €. Die auf die Gehälter entfallenden
Sozialkosten sind wie die Gehälter selbst als fix anzusehen. Für das neue Jahr ergeben sich nun die
folgenden fixen und variablen Kosten:
Materialkosten
Löhne
Gehälter
Soziale Kosten
Reparaturkosten
Abschreibungen
Verschiedene Kosten
gesamt
84.000 €
147.000 €
63.000 €
31.500 €
14.000 €
19.000 €
10.000 €
368.500 €
variabel
84.000 €
147.000 €
22.050 €
8.400 €
261.450 €
fix
- €
- €
63.000 €
9.450 €
5.600 €
19.000 €
10.000 €
107.050 €
Berechnung der variablen Stückkosten:
kv = Kv / x
kv = (84.000 + 147.000 + 22.050 + 8.400) / 30.000
kv = 8,715
Berechnung der Kostenfunktion:
K = Kf + kv * x
K = (63.000 + 9.450 + 5.600 + 5.600 + 19.000 + 10.000) + 8,715x
K = 107.050 + 8,715x
Der Break-Even-Point liegt dort, wo die Erlöse gleich den Kosten sind:
E=K
13x = 107.050 + 8,715x
Industriemeister
-2-
14.12.2013
4,285x = 107.050
x = 24.982,50
Der Break-even-point ist bei einer Ausbringungsmenge von 24.982,50 – aufgerundet also
24.983 Stück - erreicht.
Aufgabe 4
Ermittlung Break-Even-Menge und Break-Even-Umsatz
Vor der Durchführung einer Break-Even-Analyse muss die Kostenfunktion bekannt sein, es müssen
also fixe und variable Kosten bestimmt werden. Anhand der Daten aus der Aufgabenstellung kann
hierfür das Differenzen-Quotienten-Verfahren benutzt werden.
Die Material- und Fertigungseinzelkosten sind immer variabel:
128.000 / 16.000 = 8 € (Materialeinzelkosten pro Stück)
160.000 / 16.000 = 10 € (Fertigungseinzelkosten pro Stück)
Materialgemeinkosten (variabel/Stück)
66.000 - 54.000 12.000
=
=3€
4.000
20.000 - 16.000
Materialgemeinkosten (fix)
K = Kf + kv * x
54.000 = Kf + 3 * 16.000
Kf + 48.000 = 54.000
Kf = 6.000 €
Fertigungsgemeinkosten (variabel/Stück)
112.000 - 92.000 20.000
=
=5€
4.000
20.000 - 16.000
Fertigungsgemeinkosten (fix)
K = K f + kv * x
92.000 = Kf + 5 * 16.000
Kf + 80.000 = 92.000
Kf = 12.000 €
Verwaltungs- und Vertriebsgemeinkosten (variabel/Stück)
48.000 - 40.000 8.000
=
=2€
20.000 - 16.000 4.000
Verwaltungs- und Vertriebsgemeinkosten (fix)
K = K f + kv * x
40.000 = Kf + 2 * 16.000
Kf + 32.000 = 40.000
Kf = 8.000 €
Aus diesen Berechnungen für die einzelnen Kostenarten kann die Gesamtkostenfunktion erstellt werden: Die variablen und fixen Kosten für die einzelnen Kostenarten betragen:
Industriemeister
-3-
14.12.2013
Materialeinzelkosten
Fertigungseinzelkosten
Materialgemeinkosten
Fertigungsgemeinkosten
Verwaltungs- und Vertriebsgemeinkosten
Summe
variabel
8€
10 €
3€
5€
2€
28 €
fix
6.000 €
12.000 €
8.000 €
26.000 €
Hieraus ergibt sich die folgende Kostenfunktion:
K = 26.000 + 28x
Da der Verkaufspreis für das Produkt 30,00 € beträgt, lautet die Erlösfunktion:
E = 30x
Berechnung der Break-Even-Menge:
30x = 26.000 + 28x
2x = 26.000
x= 13.000
Die Break-Even-Menge liegt bei 13.000 Outputeinheiten.
Der Break-Even-Umsatz beträgt:
E = 30,00 * 13.000 = 390.000 €
Ermittlung der langfristigen Preisuntergrenze.
Die langfristige PU liegt bei dem Preis, der die Stückkosten gerade noch deckt, bei dem also gilt:
p=k
Die Stückkosten sind bei linearem Verlauf der Gesamtkostenfunktion an der Kapazitätsgrenze am geringsten.
Berechnung der Stückkosten an der Kapazitätsgrenze:
k=
K Kf + kv * x 26.000 + 28 * 22.000 26.000 + 616.000 642.000
=
=
=
=
= 29,18 €
x
22.000
22.000
22.000
x
Der Marktpreis darf bis auf 29,18 € sinken, ohne dass die Produktion aus Kostengründen eingestellt
wird.
Aufgabe 5
Bei linearem Kostenverlauf sind die Grenzkosten gleich den variablen Stückkosten. Der Stückdeckungsbeitrag bis einschl. 15.000 Outputeinheiten beträgt also:
P - kv = 17 - 12 = 5 €
Der Gesamtdeckungsbeitrag der ersten 15.000 Einheiten beträgt dann:
15.000 * 5 = 75.000 €
Der Stückdeckungsbeitrag für die nächsten 3.000 Einheiten verringert sich wegen des sinkenden
Marktpreises auf 4 €. Die nächsten 3.000 verkauften Einheiten leisten also einen Gesamtdeckungsbeitrag von:
3.000 * 4 = 12.000 €
Die ersten 18.000 verkauften Einheiten leisten also den folgenden Beitrag zur Deckung des Fixkostenblocks:
75.000 + 12.000 = 87.000 €
Industriemeister
-4-
14.12.2013
Es verbleiben noch 13.000 € nicht gedeckte Fixkosten. Da der Stückdeckungsbeitrag über 18.000 Einheiten auf 2 € sinkt müssen noch
13.000 / 2 = 6.500
weitere Einheiten produziert werden, um den Break-Even-Point zu erreichen.
Insgesamt liegt die Break-Even-Menge also bei
15.000 + 3.000 + 6.500 = 24.500 Outputeinheiten.
Ab 24.501 Outputeinheiten wird ein Stückgewinn von 2 erzielt. Es müssen also weitere 5.000 (insgesamt also 29.500) Einheiten produziert und verkauft werden, um einen Gewinn von 10.000 € zu erzielen.
Preisuntergrenze
1. Die kurzfristige Preisuntergrenze liegt dort, wo die variablen Stückkosten gerade noch gedeckt
sind, wo also p = kv gilt.
Begründung: Kurzfristig lassen sich Fixkosten nicht abbauen. Es entstehen dem Unternehmen
also Verluste in Höhe der Fixkosten sowohl bei Fortführung wie auch bei Einstellung der Produktion. Wenn also die Aussicht besteht, dass die Preise in Kürze wieder anziehen, kann aus kostenrechnerischer Sicht die Produktion weitergeführt werden.
Um die Höhe der kurzfristigen Preisuntergrenze zu ermitteln, müssen die variablen Stückkosten
errechnet werden:
Wenn eine Outputerhöhung um 5.000 Einheiten (von 15.000 auf 20.000) zu einer Kostensteigerung um 10.000 € (von 40.000 auf 50.000) führt, so verursacht jede zusätzliche Outputeinheit
eine Kostensteigerung um 2 € (10.000 / 5.000 = 2). Also betragen die variablen Stückkosten 2 €.
Damit liegt der Preis, bei dem kurzfristig die Produktion beibehalten werden kann, bei 2 €.
50.000 - 40.000
=2€
20.000 - 15.000
2. Die langfristige Preisuntergrenze ist gleich den Stückkosten des Unternehmens. Zur Ermittlung
der langfristigen Preisuntergrenze muss zunächst das Minimum der Stückkosten ermittelt werden. Das Minimum der Stückkosten liegt bei linearem Kostenverlauf an der Kapazitätsgrenze des
Unternehmens. Es muss also die Ermittlung der Stückkosten an der Kapazitätsgrenze (25.000
Outputeinheiten) erfolgen:
kPU = kv =
Hierzu müssen zunächst die Fixkosten ermittelt werden:
Bei einer Produktion von 20.000 Einheiten belaufen sich die variablen Kosten auf 2 * 20.000 =
40.000 €. Bei 20.000 Einheiten belaufen sich die Gesamtkosten auf 50.000 €. Also betragen die
Fixen Kosten:
Kf = K – Kv = 50.000 – 40.000 = 10.000
Stückkosten an der Kapazitätsgrenze (bei 25.000 Einheiten):
Kf + kv * x 10.000 + 2 * 25.000
=
= 2,40 €
25.000
x
Die langfristige Preisuntergrenze liegt also bei 2,40 €. Bei jedem darunter liegenden Marktpreis
kommt das Unternehmen in die Verlustzone und muss langfristig die Produktion einstellen.
k=
3. Die kurzfristige Preisuntergrenze entspricht nach wie vor den variablen Stückkosten, sie liegt also
bei 2 €.
Die langfristige Preisuntergrenze wird neu berechnet:
Industriemeister
-5-
14.12.2013
k=
Kf + kv * x 10.000 + 2 * 12.000
=
= 2,83 €
12.000
x
Die langfristige Preisuntergrenze liegt bei 2,83 €, wenn nur 12.000 Einheiten abgesetzt werden
können.
Industriemeister
-6-
14.12.2013