Formelsammlung zur Kostenrechnung

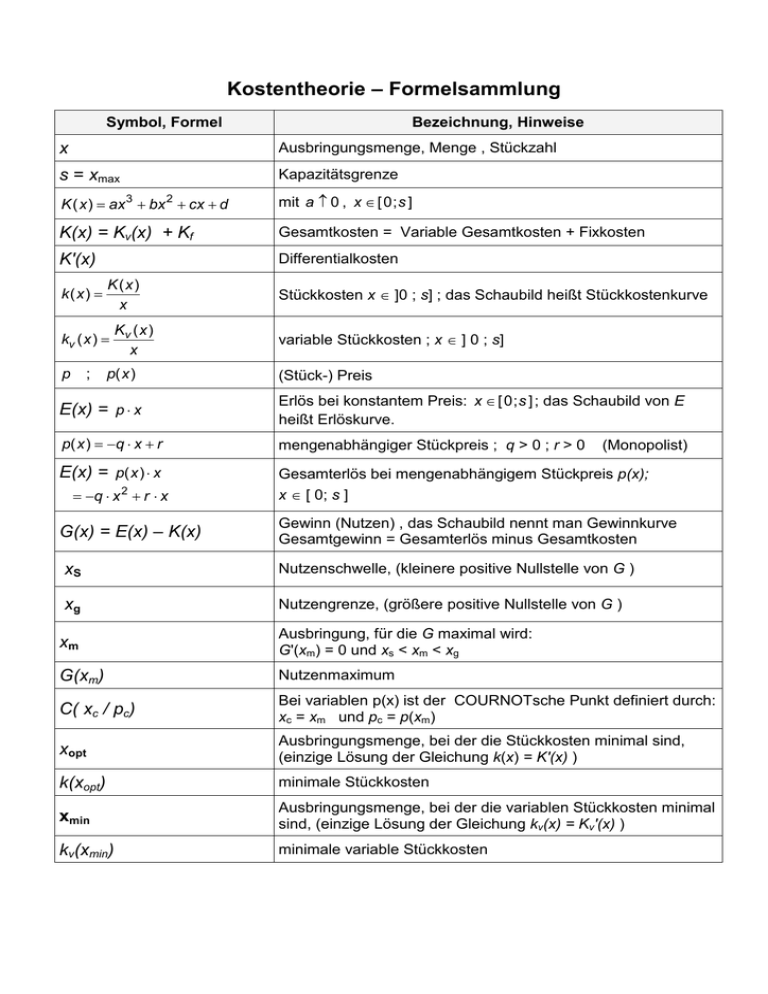
Kostentheorie – Formelsammlung
Symbol, Formel
Bezeichnung, Hinweise
x
Ausbringungsmenge, Menge , Stückzahl
s = xmax
Kapazitätsgrenze
K ( x ) = ax 3 + bx 2 + cx + d
mit a ≠ 0 , x ∈ [ 0; s ]
K(x) = Kv(x) + Kf
Gesamtkosten = Variable Gesamtkosten + Fixkosten
K'(x)
Differentialkosten
k(x) =
K(x)
x
kv ( x ) =
p
;
Kv ( x )
x
p( x )
Stückkosten x ∈ ]0 ; s] ; das Schaubild heißt Stückkostenkurve
variable Stückkosten ; x ∈ ] 0 ; s]
(Stück-) Preis
E(x) = p ⋅ x
Erlös bei konstantem Preis: x ∈ [ 0; s ] ; das Schaubild von E
heißt Erlöskurve.
p( x ) = −q ⋅ x + r
mengenabhängiger Stückpreis ; q > 0 ; r > 0
E(x) = p( x ) ⋅ x
Gesamterlös bei mengenabhängigem Stückpreis p(x);
x ∈ [ 0; s ]
= −q ⋅ x + r ⋅ x
2
G(x) = E(x) – K(x)
(Monopolist)
Gewinn (Nutzen) , das Schaubild nennt man Gewinnkurve
Gesamtgewinn = Gesamterlös minus Gesamtkosten
xS
Nutzenschwelle, (kleinere positive Nullstelle von G )
xg
Nutzengrenze, (größere positive Nullstelle von G )
xm
Ausbringung, für die G maximal wird:
G'(xm) = 0 und xs < xm < xg
G(xm)
Nutzenmaximum
C( xc / pc)
Bei variablen p(x) ist der COURNOTsche Punkt definiert durch:
xc = xm und pc = p(xm)
xopt
Ausbringungsmenge, bei der die Stückkosten minimal sind,
(einzige Lösung der Gleichung k(x) = K'(x) )
k(xopt)
minimale Stückkosten
xmin
Ausbringungsmenge, bei der die variablen Stückkosten minimal
sind, (einzige Lösung der Gleichung kv(x) = Kv'(x) )
kv(xmin)
minimale variable Stückkosten