Geometrie - Gymnasium Scheinfeld

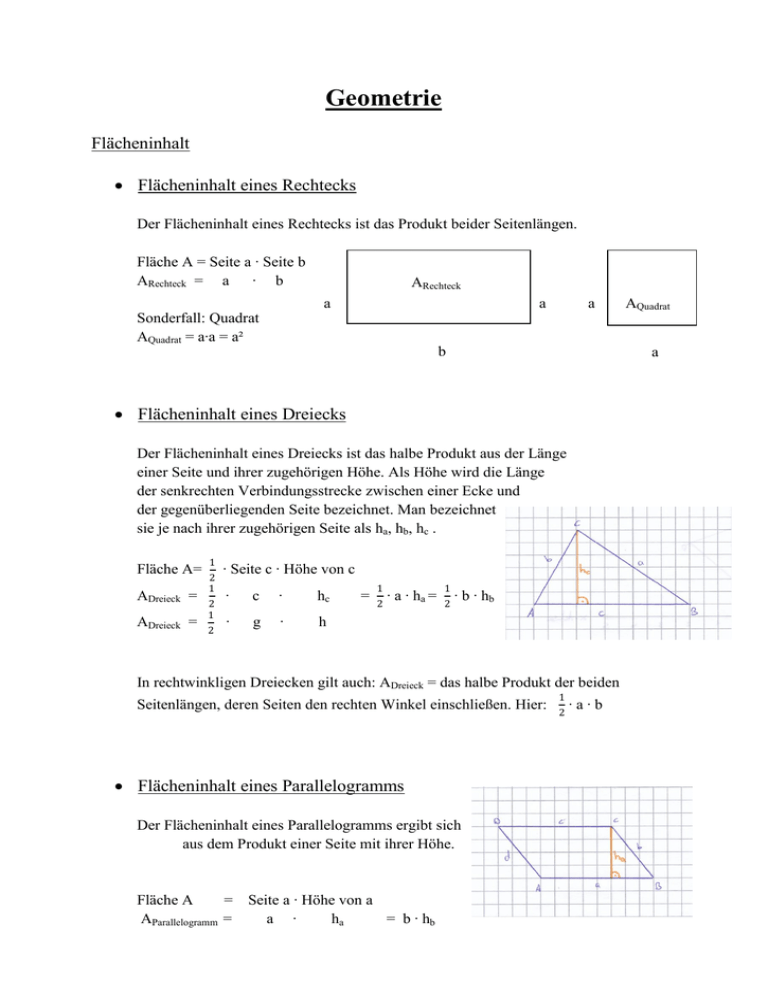
Geometrie
Flächeninhalt
 Flächeninhalt eines Rechtecks
Der Flächeninhalt eines Rechtecks ist das Produkt beider Seitenlängen.
b
Fläche A = Seite a ∙ Seite b
ARechteck = a ∙ b
ARechteck
a
Sonderfall: Quadrat
AQuadrat = a∙a = a²
a
a
a
b
a
 Flächeninhalt eines Dreiecks
Der Flächeninhalt eines Dreiecks ist das halbe Produkt aus der Länge
einer Seite und ihrer zugehörigen Höhe. Als Höhe wird die Länge
der senkrechten Verbindungsstrecke zwischen einer Ecke und
der gegenüberliegenden Seite bezeichnet. Man bezeichnet
sie je nach ihrer zugehörigen Seite als ha, hb, hc .
Fläche A=
ADreieck =
ADreieck =
1
2
1
2
1
2
AQuadrat
∙ Seite c ∙ Höhe von c
∙
c
∙
hc
∙
g
∙
h
=
1
2
∙ a ∙ ha =
1
2
∙ b ∙ hb
In rechtwinkligen Dreiecken gilt auch: ADreieck = das halbe Produkt der beiden
Seitenlängen, deren Seiten den rechten Winkel einschließen. Hier:
 Flächeninhalt eines Parallelogramms
Der Flächeninhalt eines Parallelogramms ergibt sich
aus dem Produkt einer Seite mit ihrer Höhe.
Fläche A
= Seite a ∙ Höhe von a
AParallelogramm =
a ∙
ha
= b ∙ hb
1
2
∙a∙b
 Flächeninhalt eines Trapezes
Ein Trapez ist eine Fläche, die zwei zueinander parallele Seiten besitzt. Die Fläche des
Trapezes ist das Produkt aus seiner Mittellinie und ihrer Höhe.
Die Mittellinie m ist die Hälfte der Summe der Seitenlängen der beiden
zueinander parallelen Seiten.
m = 0,5 ∙ ( a + c )
Fläche = Mittellinie ∙ Ihre Höhe
ATrapez =
m
∙
ha
 Flächeninhalt von Vielecken
Um die Fläche eines Vielecks zu berechnen zerlegt
man es in Dreiecke und addiert die Flächeninhalte
dieser Dreiecke.
Volumen
 Volumeneinheiten
∙10
Länge
mm
∙10
cm
∙100
Fläche
Volumen
mm
2
dm
∙100
cm
2
∙1000
3
3
cm
m
∙100
dm
∙1000
mm
∙10
2
m2
∙1000
dm3
m3
Das 1000-fache einer Volumeneinheit ergibt die nächstgrößere Volumeneinheit.
UZ:
m -> km
1000
m2 -> a
100
104
m2 -> ha
106
m2 -> km2
 Volumen eines Quaders
c
Das Volumen eines Quaders ist
gleich dem Produkt aller Seiten.
b
VQuader = a ∙ b ∙ c
Volumen = Länge ∙ Breite ∙ Höhe
Sonderfall: Würfel: Ein Würfel ist ein
dessen Seiten gleich lang sind.
VWürfel = a ∙ a ∙ a = a3
a
Quader,
a
a
a
 Volumen eines Prismas
Man kann jedes Prisma durch einen senkrechten
Schnitt in zwei rechtwinklige Prismen zerlegen.
Das Volumen eines Prismas errechnet man also
aus dem Produkt der Fläche der dreieckigen
Seite und der Tiefe des Prismas.
VPrisma = 0,5 ∙
b ∙
hb
∙
t
=
ADreieck
∙
t
Volumen = 0,5 ∙ Seite b ∙ Höhe von b ∙ Tiefe
 Volumen verschiedener Körper
Das Volumen eines Körpers kann man rechnerisch bestimmen, indem man
-den Körper in Quader zerlegt
-den Körper zerlegt und zu einem Quader zusammen fügt
-den Körper in Prismen zerleg
Oberflächeninhalt
Um die Oberfläche eines Körpers zu erhalten, addiert man die Flächen der Seiten des
Körpers.
Bsp.:
Quader: OQuader = 2∙(a∙b + a∙c + b∙c)
Würfel: OWürfel = 6∙a2
Schrägbilder
Um einen Körper als Schrägbild darzustellen, befolgt man
folgende drei Schritte:
1. Zeichne die Vorderfläche in wahrer Größe.
2. Zeichne die nach hinten verlaufenden
Seitenkanten schräg und verkürzt, sowie
parallel zueinander ein.
Standard: 1LE->0,5nach rechts und
0,5 nach oben
3. Verbinde die Enden der nach hinten
verlaufenden Seitenkanten.
Beachte: Kanten, die man eigentlich nicht sehen kann, werden gestrichelt eingezeichnet.