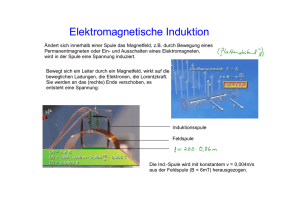
Übungen zu Experimentalphysik II

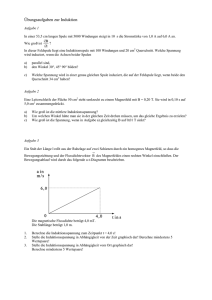
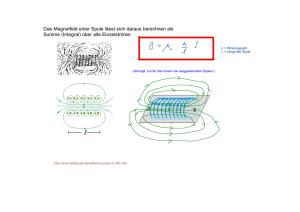
Übungen zu Experimentalphysik II
Prof. Dr. G. Abstreiter
Blatt 8
Ausgabe:
Besprechung:
13.6.2002
17.6. – 20.6.2002
SS 2002
Bonus: In der Woche 17.6. - 20.6.2002 wird das dritte Blatt mit Bonusaufgaben ausgegeben.
Aufgabe 1: Induktion in einer Leiterschleife
Eine quadratische Leiterschleife der Fläche A rotiert in einem magnetischen Feld B mit
konstanter Winkelgeschwindigkeit ω mit ω⊥B, wobei die Drehachse in der Ebene der
Schleife liegt.
a) Berechnen Sie die an den Enden der Leiterschleife anliegende Induktionsspannung.
Stellen Sie deren zeitlichen Verlauf graphisch dar.
b) Nun soll die Schleife aus (a) durch 3 jeweils um 120° versetzte Schleifen ersetzt werden,
die um eine gemeinsame Kante rotieren. Geben Sie die induzierten Spannungen in den
einzelnen Schleifen an und stellen Sie ihren zeitlichen Verlauf graphisch dar. Wie groß ist
die Summe der induzierten Spannungen?
Aufgabe 2: Bewegung eines stromdurchflossenen Drahtes
Ein Metalldraht der Masse m und dem elektrischen Widerstand R gleitet reibungsfrei auf zwei
parallelen Metallschienen (Abstand d) gemäß der Skizze in einem zeitlich konstanten
homogenen Magnetfeld der Flußdichte B.
a) Der Generator G liefert einen
konstanten Strom I. Stellen Sie die
Differentialgleichung
für
die
Bewegung des Metalldrahtes auf und
berechnen Sie seine Geschwindigkeit
v(t).
b) Der Generator G wird nun durch eine
Batterie ersetzt, die eine konstante
Spannung UB liefert. Bestimmen Sie
die im Metalldraht induzierte
Spannung Ud und den induzierten Strom Id, wenn sich der Draht mit der Geschwindigkeit
v entlang der Metallschiene bewegt.
c) Stellen Sie die Bewegungsgleichung für den Fall (b) auf und bestimmen Sie v(t) und die
Endgeschwindigkeit ve.
d) Zeigen Sie, daß beim Erreichen der Endgeschwindigkeit im Metalldraht kein Strom fließt.
Aufgabe 3: Induktivität von Spulen
In einer langen Feldspule (l1 = 1 m) vom Durchmesser 5 cm mit 3500 Windungen befindet
sich eine kleine Spule, deren Achse parallel zu der Feldspule steht. Sie hat einen Durchmesser
von 2 cm und 80 Windungen.
a) Zunächst wird die Feldspule von I = 3 A durchflossen. Wie groß ist deren
Selbstinduktivität L11 und Energieinhalt W?
b) Welche Spannung U wird zwischen den Enden der kleinen Spule beobachtet, wenn
während 5 Sekunden die Stromstärke der Feldspule gleichmäßig von 0 auf 3 A
hochgeregelt wird? Berechnen Sie dazu die wechselseitige Induktivität L12.
a) Die Enden der Feldspule werden kurzgeschlossen, und danach wird die Spannungsquelle
abgeklemmt. Nach welchem Gesetz nimmt die Induktionsspannung ab? Wie groß ist sie
zu Beginn des Vorgangs, wenn der ohmsche Widerstand der Spule 150 Ω beträgt?