Räumliche Koordinatensysteme

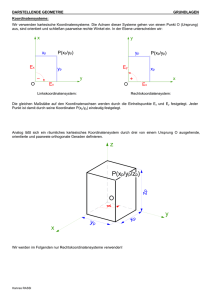
001
Lineare Algebra – Analytische Geometrie
Räumliche
Koordinatensysteme
Arbeitsblatt
Räumliche Koordinatensysteme
In der Ebene beschreibt man die Lage von Punkten in einem Koordinatensystem mit zwei Zahlen, den Koordinaten. Für Punkte im Raum benötigt man ein Koordinatensystem mit drei Achsen. Eine wirklichkeitsgetreue Darstellung verlangt ein dreidimensionales Modell. Am anschaulichsten sind Normalbilder. Sie zeigen Figuren so, wie
man sie aus großer Entfernung wirklich sieht. Wie Koordinatensysteme aussehen, hängt von der Blickrichtung ab.
Es gibt unendlich viele Ansichten. Beim Zeichnen verwendet man jedoch nur einige, nämlich:
1. Isometrie
2.
3.
4.
5.
In der Zeichnung sind alle drei Einheiten gleich lang und die Winkel zwischen den Achsen 1200.
Dimetrie
In der Zeichnung sind zwei Einheiten gleich lang und die dritte halb so lang. Die x3-Achse geht senkrecht nach oben, die x2-Achse ist 70, die x1-Achse 420 gegen die Waagrechte geneigt. Diese Art der
Darstellung wird hauptsächlich in der Technik verwendet.
Trimetrie
In der Zeichnung sind alle Einheiten verschieden lang. Für das Zeichnen auf Karopapier eignen sich besonders solche Systeme, bei denen die Einheitsmarken auf Gitterpunkten liegen.
Schrägbilder
Die x3-Achse geht senkrecht nach oben, die x2-Achse waagrecht nach rechts und die x1-Achse unter 450
gegen die Waagrechte nach vorn. Die Einheiten wählt man so, dass die Einheitsmarken auf Gitterpunkten
des Karopapiers liegen.
Standardschrägbild
Für unseren Gebrauch verwenden wir ein spezielles Schrägbild-Koordinatensystem. Die x3-Achse geht
senkrecht nach oben, die x1-Achse waagrecht nach rechts und die x2-Achse vom Koordinatenursprung
zwei Karokästchen nach rechts, ein Karokästchen nach oben.
Einheiten: x3-Achse und x1-Achse zwei Karokästchen eine Einheit, auf der x2-Achse alle 1,5 Karokästchen eine Einheit.
Aufgaben:
1. Zeichne in je ein Koordinatensystem einen Würfel mit 5LE Kantenlänge, bei dem vordere, untere, linke
Eckpunkt im Koordinatenursprung liegt.
2. Zeichne in das Standardschrägbild einen Würfel der Kantenlänge 6LE, bei dem der Koordinatenursprung
im Mittelpunkt des Würfels liegt.
3. Beschreibe die Menge aller Punkte (x1|x2|x3), für die gilt:
a.
x2 = 0
b.
x3 = 0 ∧ x 2 = 1
c.
0 ≤ x1 ≤ 1
4. A(6|3|0), B(3|6|0), C(0|6|3), D(0|3|6), E(3|0|6) und F(6|0|3) sind die Ecken eines ebenen, regelmäßigen
Sechsecks. Zeichne das Sechseck und seine senkrechten Projektionen auf die Koordinatenebenen.
5. Gegeben sind die Punkte A(6|4|1), B(4|6|0), C(5|8|2), D(7|6|3), E(4|3|3), F(2|5|2), G(3|7|4), H(5|5|5).
ABCD ist die Grundfläche, EFGH die Deckfläche eines Würfels.
a. Zeichne den Würfel.
b. Zeichne das Spiegelbild des Würfels bezüglich der x1-x2-Ebene.
c. Zeichne das Spiegelbild des Würfels bezüglich des Koordinatenursprungs.