Darstellung im Koordinatensystem – Lösungen
Werbung
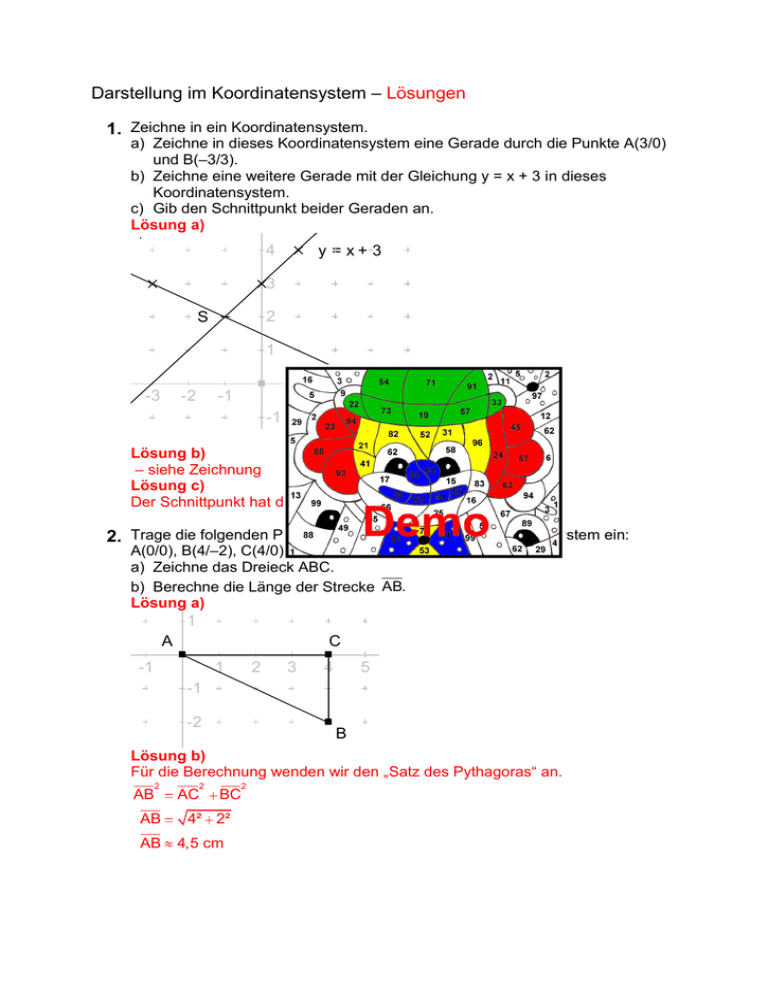
Darstellung im Koordinatensystem – Lösungen 1. Zeichne in ein Koordinatensystem. a) Zeichne in dieses Koordinatensystem eine Gerade durch die Punkte A(3/0) und B(–3/3). b) Zeichne eine weitere Gerade mit der Gleichung y = x + 3 in dieses Koordinatensystem. c) Gib den Schnittpunkt beider Geraden an. 5 Lösung a) 4 y = x+ 3 3 2 S 1 -4 -3 -2 -1 1 2 3 4 -1 Lösung b) – siehe Zeichnung Lösung c) Der Schnittpunkt hat die Koordinate S(–1/2) 2. Trage die folgenden Punkte in ein rechtwinkliges Koordinatensystem ein: A(0/0), B(4/–2), C(4/0). a) Zeichne das Dreieck ABC. b) Berechne die Länge der Strecke AB. 2 Lösung a) 1 A -2 C -1 1 2 3 4 5 -1 -2 B Lösung b) Für die Berechnung wenden wir den „Satz des Pythagoras“ an. AB 2 AB AB 2 AC 2 BC 4² 2² 4,5 cm 3. Zwei Klassen benachbarter Schulen begegneten sich am Wandertag. a) Beide Klassen beginnen die Wanderung um 8.00 Uhr. Wie weit sind sie zu diesem Zeitpunkt voneinander entfernt? b) Um wie viel Uhr trafen sich die beiden Klassen? c) Wie viele Kilometer wanderte jede Klasse bis zum Treffpunkt? Lösung a) Die Klassen sind 20 km voneinander entfernt. Lösung b) Die Klassen treffen sich um 10:15 Uhr. Lösung c) Für die Berechnung wenden wir den „Satz des Pythagoras“ an. Klasse 8 : x² 8,5² 9² x 12,34 km Klasse 9 : y² 11,5² 9² y 14,6 km 4. Zeichne ein rechtwinkliges Koordinatensystem. a) Eine Gerade verläuft durch die Punkte A(–2/3) und B(4/0). Zeichne diese Gerade in das Koordinatensystem. b) Zeichne eine weitere Gerade mit der Gleichung y = 2x – 4 in dasselbe Koordinatensystem. c) Gib die Koordinaten des Schnittpunktes S beider Geraden an. 4 Lösung a) 3 A 2 1 B -3 -2 -1 1 -1 -2 -3 -4 2 3 4 5 6 Lösung b) s. Zeichnung Lösung c) S=B 5. Zeichne ein Koordinatensystem. a) Zeichne das Dreieck ABC mit A(3/3), B(–2/3) und C(–2/–1) in dieses Koordinatensystem. (1 Einheit entspricht 1 cm) b) Berechne den Flächeninhalt des Dreiecks ABC. c) Zeichne einen Punkt D so, dass ein Parallelogramm entsteht. Gib die Koordinaten von 4 D an. Lösung a) B 3 A 2 1 -4 -3 -2 C -1 1 2 3 -1 Lösung b) A = 10 cm² Lösung c) s. Zeichnung – es entsteht als besonderes Parallelogramm ein Rechteck