Dynamik der gKB: die Zentripetalkraft

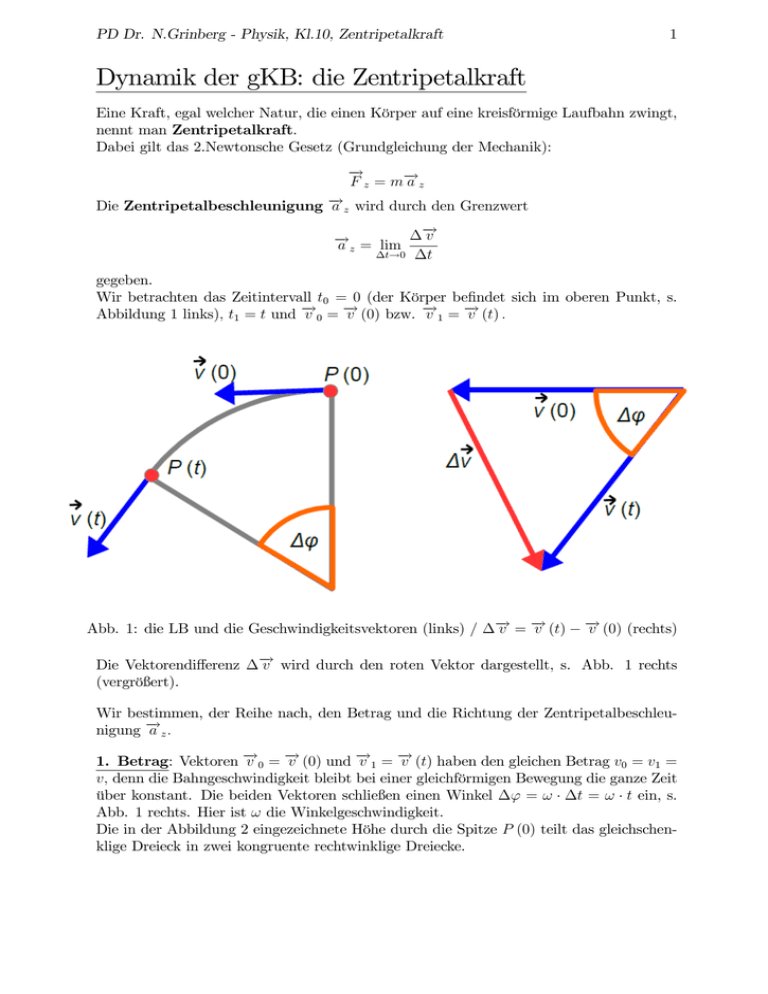
PD Dr. N.Grinberg - Physik, Kl.10, Zentripetalkraft
1
Dynamik der gKB: die Zentripetalkraft
Eine Kraft, egal welcher Natur, die einen Körper auf eine kreisförmige Laufbahn zwingt,
nennt man Zentripetalkraft.
Dabei gilt das 2.Newtonsche Gesetz (Grundgleichung der Mechanik):
!
F z = m!
az
Die Zentripetalbeschleunigung !
a z wird durch den Grenzwert
!
a z = lim
t!0
!
v
t
gegeben.
Wir betrachten das Zeitintervall t0 = 0 (der Körper be…ndet sich im oberen Punkt, s.
Abbildung 1 links); t1 = t und !
v0=!
v (0) bzw. !
v1=!
v (t) :
Abb. 1: die LB und die Geschwindigkeitsvektoren (links) /
Die Vektorendi¤erenz
(vergröß
ert).
!
v =!
v (t)
!
v (0) (rechts)
!
v wird durch den roten Vektor dargestellt, s. Abb. 1 rechts
Wir bestimmen, der Reihe nach, den Betrag und die Richtung der Zentripetalbeschleunigung !
a z:
1. Betrag: Vektoren !
v0=!
v (0) und !
v1=!
v (t) haben den gleichen Betrag v0 = v1 =
v; denn die Bahngeschwindigkeit bleibt bei einer gleichförmigen Bewegung die ganze Zeit
über konstant. Die beiden Vektoren schließ
en einen Winkel ' = !
t = ! t ein, s.
Abb. 1 rechts. Hier ist ! die Winkelgeschwindigkeit.
Die in der Abbildung 2 eingezeichnete Höhe durch die Spitze P (0) teilt das gleichschenklige Dreieck in zwei kongruente rechtwinklige Dreiecke.
PD Dr. N.Grinberg - Physik, Kl.10, Zentripetalkraft
2
Betrachten wir nun das Obere Dreieck.
Es hat die Hypotenuse v0 = v und den Winkel
1
' an P (0) :
2
Die gegenüber liegende Kathete hat die Länge
Def. von Sinus:
Gegenkathete
= sin
Hypotenuse
1
2
1
2
' :
v = v sin 12 ' oder
1
1
v = 2v sin
' = 2v sin
!t :
2
2
Also gilt:
1
2
Abb. 2: Hilfskonstruktion
Der Grenzübergang liefert:
az = lim
t!0
v
= lim
t!0
t
1
!t
2
2v sin
t
:
Aus dem Mathematikunterricht soll bekannt sein, dass sin (x)
1
1
(sin0 (0) = 1). Also ist sin
!t
!t und folglich
2
2
1
!t
2
2v sin
az = lim
t
t!0
x ist für kleine x-Werte
1
! = v!:
2
= 2v
Je nachdem, welche Größ
en gegeben sind, kann man auf eine der folgenden äquivalenten
Formeln für den Betrag der Zentripetalbeschleunigung zugreifen:
az
Fz
2
=
2
T
v2
= mv! = m
= m! 2 R = m
R
2
T
2
= v!
v2
=
R
2
=! R
R
= (2 f )2 R bzw.
R = m (2 f )2 R
2. Richtung der Zentripetalbeschleunigung:
Der Vektor !
v schließ
t mit der Vertikalen
1
einen Winkel von 2 ': Die gleiche Richtung
!
v
hat natürlich auch der Quotient
:
t
Bei dem Grenzübergang für t ! 0 strebt
der Winkel 12 ' = !
t gegen 0:
Deswegen steht der Vektor !
a z senkrecht auf
!
v 0 und ist zum Mitelpunkt der Kreislaufbahn
gerichtet.
Abb. 3: Richtung von
!
v
v:
PD Dr. N.Grinberg - Physik, Kl.10, Zentripetalkraft
3
AB2 gleichförmige Kreisbewegung: Zentripetalkraft 2d
1
1
bzw. T =
T
f
2 R
= 2 Rf =
T
= !R
2
=
T
v2
= !2R =
= v! =
R
f=
v
v
!
az
2
2
T
R = (2 f )2 R:
v2
Fz = maz = mv! = m = m! 2 R = m
R
2
T
2
R = m (2 f )2 R
A1. Ein Käfer (m = 1 g) rotiert windgeschützt auf der Flügelspitze (r = 15 m) einer
Windkraftanlage, die für eine Umdrehung 2 s braucht. Mit welcher Kraft muss sich der
Käfer mit seinen kleinen Käferbeinchen an dem Flügel festhalten, damit er darauf sitzen
bleibt?
Fz = m
2
T
= 0:001
2
R
2
2
2
15
0:148 N
A2. Der Wurfhammer beim Hammerwerfen der Frauen
hat eine Masse von m = 4; 0 kg und ist 120 cm lang.
Die Armlänge beträgt 70 cm:
Vor dem Abwurf erreicht die Kugel des Hammers eine
m
Geschwindigkeit von 25 :
s
Welche Zentripetalkraft muss die Werferin auf die Kugel
des Hammers ausüben?
Vergleiche diesen Wert mit der Gewichtskraft, die die
Sportlerin erfährt, wenn ihre Masse 65 kg betragt.
v2
252
=4
= 1315:8 N
R
1:2 + 0:7
FG = mg = 65 9:81 = 637:65 N:
Fz = m
A3. Ein Hammerwerfer schwingt eine Eisenkugel der Masse 7 kg, die an einer 1; 2 m
langen Schnur hängt, mit der Geschwindigkeit v = 11 m=s bei gestreckten Armen um
seine eigene Achse (Armlänge 80 cm). Bestimme die hierfür benötigte Zentripetalkraft.
Vergleiche dein Ergebnis mit der Antwort zu Aufgabe 2.
Fz = m
v2
112
=7
= 423:5 N
R
1:2 + 0:8
PD Dr. N.Grinberg - Physik, Kl.10, Zentripetalkraft
4
AB3 gleichförmige Kreisbewegung, Dynamik 2d:
elastische Kraft / Haftreibungskraft als Zentripetalkraft
A1. Eine Kugel mit der Masse m = 100 g liegt auf einer
rotierenden Scheibe. Sie wird durch einen Faden gehalten.
Wie großmuss die Fadenkraft sein, wenn die Scheibe 30
Umdrehungen in der Minute macht und der Radius 15 cm
misst? Die Reibung ist zu vernachlässigen.
http://www.lei…physik.de/themenbereiche/kreisbewegung/lb/kreisbewegung-musteraufgabenkreisbewegung-dynamisch-kugel-schnur-0
Gegeben:
1
= 0; 5 Hz
min
m = 0; 1 kg;
R = 0; 15 m
f = 30
Daraus folgt:
Fz = m (2 f )2 R = 0:1 (2
0:5)2 0:15 = 0:148 N:
N
A2. Ein Massenstück mit m = 0; 2 kg wird auf einer Feder mit D = 0; 3
waagerecht
cm
geschleudert. Die Kreisfrequenz beträgt f = 1 Hz: Um viele cm verlängert sich die Feder,
wenn ihre Länge ohne Belastung 30 cm ausmacht. Die Gewichtskraft ist zu vernachlässigen.
Gegeben:
m = 0; 2 kg
N
D = 30
m
f = 1 Hz
l0 = 0; 3 kg
Lösungsplan: In diesem Fall ist Fz die elastische Kraft, diese wird durch
Fel = D l (Betrag)
gegeben. Hier ist
x = l:
Es ist einerseits
l die Verlängerung der Feder. Wir bezeichnen zwecks Abkürzung
Fel = Dx = 30x;
andererseits gilt
R = l0 + x
Fz = m (2 f )2 R = 0:2 (2
1)2 (0:3 + x) :
Gleichsetzen ergibt:
Fz = Fel
0:2 (2
2
1) (0:3 + x) = 30x
PD Dr. N.Grinberg - Physik, Kl.10, Zentripetalkraft
5
Au‡ösen nach x :
2:368 7 + 7:895 7x = 30x
2:368 7 = 22:104x
2:368 7
x=
= 0:107 16
22:104
Allgemeine Lösung:
11 cm:
Dx = m (2 f )2 (l0 + x)
Dx = m (2 f )2 l0 + m (2 f )2 x
m (2 f )2 x = m (2 f )2 l0
D
x=
m (2 f )2
l0 :
D m (2 f )2
Daraus folgt insbesondere die Bedingung
m (2 f )2 > 0
D
1
f<
2
oder
r
D
m
r
D
;
m
was auf die Grenzen des Modells ohne Gewichtskraft hinweist.
!<
A3. An einer Straß
enkreuzung bewegen sich Autos in einem Kreis um einen Blumenbett
mit dem Radius R = 10 m: Bei welcher Höchstgeschwindigkeit kriegen die Autos noch
die Kurve beim guten Wetter ( H = 0; 81)?
Gegeben:
R = 10 m
H = 0; 81:
Lösungsplan: In diesem Fall ist Fz die Haftreibungskraft, diese wird durch
FHR =
H
mg
gegeben. Gleichsetzen von FZ und FHR , Kürzen von m und Au‡ösen nach v = vmax
ergibt:
v2
m =
R
vmax =
H mg
p
H gR
=
p
m
km
0:81 9:81 10 = 8:914 1
= 32:09
:
s
h
A4. Mit welcher Geschwindigkeit kann der Oststadtkreisel (R = 26; 3 m)
a) bei trokener Fahrbahn (
H
b) bei nasser Fahrbahn (
= 0; 40)
H
= 0; 65)
höchstens durchfahren werden? Gib die Antworten in
km
an.
h
Lsg:
b) vmax
p
p
km
h
p
p
km
=
0:40 9:81 26:3 3:6 = 36:572
:
H gR =
h
a) vmax =
H gR
=
0:65 9:81 26:3 3:6 = 46:62