Die Zahl e, Differentiale und e-Funktionen - system

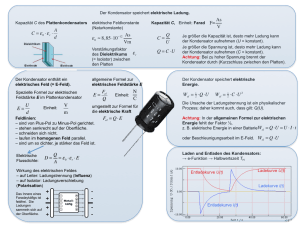
Dieter Holzhäuser
http://www.system-maker.de
E-Mail: [email protected]
Überarbeitung: 11.05.2012
Die Zahl e, Differentiale und e-Funktionen
Was bedeutet die berühmte Zahl e und warum kommt sie bei vielen physikalischen und
technischen Vorgängen vor?
Wie oft der Durchmesser in den Umfang eines Kreises passt, wird durch die Zahl π (pi)
angegeben. Was aber die Zahl e bedeutet, ist nicht so einfach zu sagen.
In der Praxis verbirgt sich die Zahl e (Eulersche Zahl) meistens in e-Funktionen.
Üblicherweise wird ein Problem als gelöst betrachtet, wenn man die Funktion, nach der ein
Vorgang abläuft, mit Hilfe von Differentialquotienten und der Infinitesimalrechnung
gefunden hat. Auch wenn diese Funktion eine e-Funktion ist, erfährt man dabei kaum etwas
über das Wesen der Zahl e.
Das Kapitalwachstum ist eine Ausnahme. Es öffnet den Blick und gibt die Möglichkeit, die
Verwendung von Differentialen an vergleichbaren Beispielen zu zeigen.
Vom Zinseszins zur Zahl e
Betrachten wir zunächst das Wachstum von Kapital an einem Beispiel: Ein Kapital a, das
mit jährlich 5% verzinst wird, hat sich nach 20 Jahren verdoppelt, wenn die Zinsen in einer
Zahlung am Ende der Laufzeit zugeschlagen werden.
Die Zahlung der Zinsen kann in beliebigen Zeitintervallen erfolgen, auch wenn der Zinsfuß sich
auf ein Jahr bezieht.
Werden die Zinsen in 2 Zahlungen zugeschlagen, wird das aktuell vorhandene Kapital um
die Hälfte größer. Der Faktor ist 1,5 oder (1+1/2). Und dieser Faktor gilt sowohl in der
ersten Hälfte des Zeitraums als auch in der zweiten. Für den ganzen Zeitraum ist der Faktor
1
1
1 2
1 n
dann (1+ )⋅( 1+ )=(1+ ) Bei n Zahlungen ist der Faktor (1+ ) .
n
2
2
2
Würde jährlich eine Zinszahlung erfolgen, was die übliche Praxis ist, würde das Kapital nach
1 20
5 20
) =a 0⋅( 1+
) =a 0⋅2,65.. betragen. Da der Zinsfuß (5%) in der
20
100
p n
Formel auftaucht, gilt für einen Zinsfuß p und n Jahre a=a0⋅(1+
) , und das ist die
100
20 Jahren a=a0⋅(1+
bekannte Zinseszinsformel.
Sind beispielsweise 1000 Zinszahlungen in 20 Jahren vorgesehen, ergibt sich ein Kapital
von a=a0 (1+
1 1000
) =a 0⋅2,716...
1000
Der Faktor, mit dem das Kapital wächst, nähert sich mit zunehmender Anzahl
Zinszahlungen einem Grenzwert, der erst bei unendlich vielen Zahlungen erreicht wird.
Dieser Grenzwert ist die Eulersche Zahl e = 2,7182... Als irrationale Zahl hat sie unendlich
viele Nachkommastellen ohne Periode.
1
Die bekannteste mathematische Formel für e lautet:
1 n
e=lim (1+ )
n
n →∞
Grenzwerte werden durch den Ausdruck lim (limes) bezeichnet, da man n in der Formel nicht
einfach durch das Zeichen für Unendlich ersetzen darf.
Das Kapitalwachstum als e-Funktion
Bleiben wir beim kontinuierlichen (praktisch aber unmöglichen) Wachstum des Kapitals. Ein
Kapital a 0 wächst in 20 Jahren um den Faktor e, in 40 Jahren um den Faktor e² und in 10
Jahren um den Faktor e 0,5 . Dieser Vorgang wird durch die Funktion a=a0⋅e x beschrieben.
Der Exponent x ist die zeitabhängige Anzahl der „Ver-e-fachungen“. Nicht das Kapital a,
sondern die reelle Zahl der Multiplikationen mit e ist der Zeit proportional.
Größen die zeitabhängig sind, werden zweckmäßig als Produkt K⋅t geschrieben, also
x =K⋅t Die Konstante K ist die Anzahl der Multiplikationen mit e in der Zeiteinheit, und t ist
die Anzahl der Zeiteinheiten.
Ganz analog ist der bei gleichförmiger Bewegung zurückgelegte Weg s das Produkt von
zurückgelegtem Weg in der Zeiteinheit und der Anzahl der Zeiteinheiten, wodurch die bekannte
Formel entsteht: Weg s = Geschwindigkeit v * Zeit t
Die e-Funktion des Kapitalwachstums lautet also: a=a0⋅e K⋅t
Um e-Funktionen einfach logarithmieren zu können, gibt es den Logarithmus zur Basis e
(natürlicher Logarithmus ln): ln (e x )=x⋅ln e =x oder e ln x = x
Bei unserem Beispiel ist nach 20 Jahren x =K⋅t=1
Mit t=20[ a ] ist K =
1 −1
[a ]
20
Die Konstante K erweist sich als der Zinsfuß von 5% . Der Faktor des jährlichen Wachstums
1
ist e K =e 20 =1,05127.. also 5,127%.
a [ Kapital ]
a [ Kapital ]
e=2,718..
−0,05⋅t
a=1⋅e
1
=0,367..
e
a=1⋅e 0,05⋅t
t [ Jahr ]
t [ Jahr ]
Die Grafik oben links zeigt den Funktionsgraphen für einen Zinsfuß von 5% und ein
Anfangskapital 1, was gleichbedeutend ist mit dem Faktor, mit dem sich ein bestimmtes
2
Anfangskapital in einer bestimmten Zeit vermehrt hat. Für 20 Jahre ist dieser Faktor
gleich e.
Die e-Funktion gilt auch für ein Kapital nach dem Beispiel zuvor, von dem kontinuierlich
kleinste Beträge weggenommen werden, die also auf ein Jahr bezogen 5% betragen. Das
Kapital des Beispiels wäre nach 20 Jahren auf den e-ten Teil zusammengeschmolzen, wie
die Grafik oben rechts zeigt. Mathematisch bedeutet das einen negativen Exponenten
von e, also K =−
1 −1
[a ]
20
Fazit: Die praktische Bedeutung der Zahl e liegt darin, dass sie als Basis in
Exponentialfunktionen auftritt, durch die Wachstums- und Schrumpfungsprozesse der
realen Welt beschrieben werden.
Warum verläuft ein Vorgang nach einer e-Funktion?
Oder, was haben Vorgänge, die nach einer e-Funktion verlaufen, gemeinsam? Diese Fragen
muss man einfach stellen, wenn man dem Wesen der Zahl e nachspürt.
Die Antwort liegt bei den winzig kleinen Zinsbeträgen, die das aktuell vorhandene Kapital
vermehren. Es wächst in einem mikroskopisch kleinen Zeitintervall Δt um einen ebenso
mikroskopisch kleinen Betrag Δa.
Mit dem Zeichen Δ (delta) wird die Veränderung bezeichnet, z.B. Δ a=a nachher −a vorher
Makroskopisch wächst das Kapital nur deshalb nach einer e-Funktion, weil sich viele dieser
mikroskopisch kleinen und doch unterschiedlich hohen Beträge summieren. Handelt es
aber nur um einem solchen mikroskopischen Vorgang, dann gilt für ihn die ganz normale
Zinsformel Δ a=a⋅K⋅Δ t . Der Zinsbetrag ist Δ a , a entspricht dem momentan vorhandenen
Kapital und K dem Zinsfuß. Man erkennt, dass der mikroskopische Zuwachs der momentan
vorhandenen Menge mit dem Faktor K proportional ist. Und das ist die Eigenschaft, die
dazu führt, dass Vorgänge nach einer e-Funktion verlaufen.
Fazit: Wachstums- und Schrumpfungsvorgänge lassen sich dann mit einer e-Funktion
beschreiben, wenn die mikroskopisch kleinen Beträge, um die sich die aktuelle Menge in
entsprechend kleinen Intervallen verändert, dieser Menge proportional sind.
Differentiale
Obwohl die Differenzen Δ a und Δ t schon mikroskopisch klein sind, man kann sie immer
noch kleiner machen. Das geht erst dann nicht mehr, wenn man festlegt, dass sie kleiner
sein sollen als jede noch so kleine absolute Zahl, aber nicht Null. Größen mit diesen
Eigenschaften werden als Differentiale bezeichnet und das Rechnen mit ihnen ist die
Infinitesimalrechnung. Das Zeichen Δ wird durch das Zeichen d ersetzt, z.B. da oder dt.
Das mikroskopische Geschehen beim Kapitalwachstum wird nun durch die Formel
da=a⋅K⋅dt beschrieben, die für jeden Punkt des Wachstumsverlaufs gilt. Das heißt, dass
diese Formel genauso wie a=a0⋅e K⋅t den Verlauf des ganzen Vorgangs ausdrückt. Allerdings
nur fast. Das Anfangskapital a 0 kommt in da=a⋅K⋅dt nicht vor, weshalb diese Formel für
jedes Anfangskapital gilt, das heißt für alle Graphen, die dem Graphen im Diagramm oben
in y-Richtung parallel sind.
Die Formel da=a⋅K⋅dt hat die Merkmale, um sie eine Differentialgleichung nennen zu
können. Unter dieser Begrifflichkeit ist a=a0⋅e K⋅t die Lösungsfunktion, was darauf hin
deutet, dass die Mathematik einen Weg kennt, aus der Differentialgleichung die
Lösungsfunktion zu ermitteln. Dieser Weg heißt Integrieren. Auch den umgekehrten gibt es.
Es ist das Differenzieren, das hier aber keine Bedeutung hat.
3
Gibt es die Differentiale wirklich?
Integrieren von
Ja, es gibt diese schwer zu begreifenden Gebilde.
Man stelle sich eine Tangente z.B. an den
Graphen vor, der das kontinuierliche
Kapitalwachstum beschreibt. Die Steigung der
Tangente ist die makroskopische Entsprechung
der Steigung, die der Graph im Berührungspunkt
hat.
Eine Steigung ist nicht ohne Steigungsdreieck
denkbar. Im Berührungspunkt (und in jedem
anderen Punkt) des Graphen muss sich daher ein
unendlich kleines Steigungsdreieck befinden.
Folglich sind auch dessen Katheten unendlich
klein. Ihre Länge kann nicht durch eine reelle
Zahl und auch nicht durch Null angegeben
werden. Deshalb muss es dafür unendlich kleine
Zahlen geben, und das sind die Differentiale wie
z.B. da und dt
Die Steigung des Graphen im Berührungspunkt
ist eine reelle Zahl (wie die Steigung einer
Straße) und entspricht dem Quotient zweier
Differentiale, dem Differentialquotient
da
dt
da=a⋅K⋅dt
Der Zweck des Integrierens ist, die Differentiale
zum Verschwinden zu bringen. Die Gleichung
wird so umgestellt, dass die Werkzeuge der
Integralrechnung auf beiden Seiten der
Gleichung angewandt werden können:
1
∫ a da=∫ K⋅dt
Ohne auf die Werkzeuge einzugehen, sieht die
Lösung so aus: ln a= K⋅t + C , wobei C die noch
zu bestimmende Integrationskonstante ist. Zur
Potenz von e erhoben ergibt sich: a=e C⋅e K⋅t
Mit dem Anfangskapital
entstehen:
C
a 0=e
und
a 0 zum Zeitpunkt t =0
a=a0⋅e K⋅t
Man sieht, dass es sich beim Integrieren um eine
ganz formale Angelegenheit handelt, aus der
kaum Erkenntnisse über das Wesen der Zahl e
zu erhalten sind.
.
Zwei unendlich kleine Zahlen stehen also für eine
reelle Zahl. Letztlich ist es dieses Phänomen, das
den Übergang zwischen der reellen und der
differentiellen Welt und damit die
Infinitesimalrechnung möglich macht.
Integrieren ist in Physik und Technik unverzichtbar, weil die Vorgänge meistens nur durch
Differentialgleichungen zu beschreiben sind.
Das Kapitalwachstum macht eine Ausnahme, weil es in der Praxis in Stufen vor sich geht,
die einer einfachen Formel folgen, ganz anders als bei physikalisch technischen Vorgängen,
die fast immer kontinuierlich sind. Das hindert aber nicht daran, sich ein infinitesimales
Steigungsdreieck für einen solchen Vorgang vorzustellen. Das Problem ist schon fast gelöst,
wenn es gelingt, den Differentialquotienten
da
zu formulieren, der sich z.B. beim
dt
Kapitalwachstum aus der einfachen Zinsformel ergeben hat.
Differentialquotienten werden auch gebildet, nicht um zu integrieren, sondern um
zweckmäßige Einsetzungen vornehmen zu können. Bei den Beispielen Kondensator und
Induktivität wird davon Gebrauch gemacht.
Jedes der folgenden Beispiele führt zu einer Differentialgleichung in der Form da=a⋅K⋅dt .
Integrieren ist nicht erforderlich, da die Lösungsfunktion a=a0⋅e K⋅t bekannt ist. Der Reiz der
Beispiele liegt vielmehr darin, den Faktor K zu bestimmen.
4
Kondensator
Der Strom, der beim Umschalten des Schalters S2 kurzzeitig fließt (siehe Schaltbild unten),
ist das zu untersuchende Phänomen, denn eigentlich dürfte kein Strom fließen, da sich
zwischen den Kondensatorplatten ein Isolator befindet. Der Kondensator wird durch diesen
Strom geladen, wenn die Spannungsquelle U2 angeschaltet wird. Die andere
Schalterstellung entlädt ihn, wobei sich die Stromrichtung umkehrt.
Die Abhängigkeit des Stromes I von der Zeit t wird also
gesucht. Der Ansatzpunkt dafür ist die Beziehung zwischen
den Differentialen dI und dt . Um sie zu finden, werden
Differentiale anderer Größen, sie sich ebenfalls mit dem
Strom ändern, benutzt.
Mit einer differentiellen Stromänderung sind am Widerstand
R1 die Spannungsänderung dU R =R⋅dI und am Kondensator
C1 die gleich große, aber entgegen gesetzte
Spannungsänderung −dU C verbunden. Also gilt:
R⋅dI =−dU C
Die Formel für die Kapazität eines Kondensators lautet:
C=
Q
UC
(Die Kapazität gibt an, mit wie viel Ladung die
Spannung von 1 V den Kondensator laden kann.) Differentiell
gilt: dU C =
dQ
−dQ
. Oben eingesetzt ergibt das: dI =
.
C
RC
Ladung und Strom sind über die Zeit verbunden. Differentiell bedeutet das: dQ= I⋅dt .
1
⋅dt . Diese Differentialgleichung
RC
1
entspricht in ihrer Form der des Kapitalwachstums, wobei K =−
ist. Die
RC
Wiederum oben eingesetzt, ergibt sich dI =−I
Lösungsfunktion ist damit:
I [ A]
I = I 0⋅e
−
1
t
RC
Die nebenstehende Grafik zeigt den Verlauf
des Stromes über der Zeit bei der
Schaltung oben.
Laden
Laden
1
−
10V
1000 Ω⋅10
I=
⋅e
1000 Ω
−6
F
t
In der Praxis spielt K keine Rolle, wohl aber
das Produkt RC = τ (tau), die Zeitkonstante.
Sie beträgt 0,001 s. Das ist die Zeit, in der
Strom auf den e-ten Teil, also etwa 3,6 mA,
abgesunken ist. Praktisch ist der Lade- bzw.
Entladevorgang nach 5τ beendet.
Auch die Spannungen an den Bauteilen sind
für die Praxis interessant, und zwar am
t [s] ]
t [s
Widerstand
Entladen
I =−
10V
⋅e
1000 Ω
−
U R =U 0⋅e
1
t
RC
−
und am Kondensator U =U (1−e
C
0
1
−
t
−6
1000 Ω⋅10 F
5
1
t
RC
)
Induktivität
An der Induktivität entsteht beim Umschalten des Schalters S1 eine Spannung, die nicht
aus einem Ohmschen Spannungsabfall herrührt, da die Spule im Idealfall den Widerstand
Null hat. Diese Spannung ist also das Phänomen, das zu untersuchen ist.
In Anlehnung an den Kondensator kann man auch bei der Induktivität sagen, dass sie
„geladen“ wird, wenn man die Spannungsquelle U1 anschaltet. Nur handelt es sich dabei
nicht um elektrische Ladung, sondern um magnetischen Fluss. An der Spule entsteht die
Spannung U L , die sich umkehrt, wenn die Induktivität bei der anderen Schalterstellung
entladen wird.
Die Abhängigkeit der Spannung U L von der Zeit t ist also
gesucht. Der Lösungsansatz dafür ist jetzt die Beziehung der
Differentiale dU L und dt .
Vergleichbar mit dem Kondensator gilt, dass eine
differentielle Spannungsänderung an der Induktivität L1 eine
gleich große, aber entgegengesetzte Spannungsänderung am
Widerstand R1 zur Folge hat. Als Formel: dU L =−dI⋅R
Die Induktivität L einer Spule ist der magnetische Fluss Φ,
den 1 A des hindurch fließenden Stromes erzeugt, was die
Φ
dΦ
Formel L=
ausdrückt, in differentieller Form: dI =
I
L
Oben eingesetzt ergibt das dU L =−
dΦ
⋅R
L
Analog zur elektrischen Ladung sind magnetischer Fluss und „angesammelte“ Spannung
über die Zeit t verbunden. In differentieller Form lautet die Formel dafür: d Φ=U L⋅dt
R
d Φ oben eingesetzt ergibt die Differentialgleichung dU L =−U L ⋅dt , deren Form der des
L
Kapitalwachstums entspricht. Die Lösungsfunktion ist demzufolge U =U ⋅e
L
0
gilt: K =−
R
− t
L
und für K
R
L
Die Grafik zeigt den Verlauf der Spannung
U L in Abhängigkeit der Zeit t. Die
Zeitkonstante ist τ = L / R = 0,001 s. In
dieser Zeit ist beim Laden U L auf 10 V / e =
3,67 V abgesunken.
U L [V ]
Laden
−
U L =10V⋅e
100 Ω
⋅t
0.1H
Praktische Bedeutung hat auch der Verlauf
der Spannung am Widerstand
−
U R =U 0⋅(1−e
t [s]
Entladen
U L =−10V⋅e
−
100 Ω
⋅t
0.1H
6
R
t
L
)
Radioaktiver Zerfall
Es ist offensichtlich, dass beim radioaktiven Zerfall in einem unendlich kleinen
Zeitintervall dt der Verlust an Teilchen dn der vorhandenen Teilchenmenge n proportional
ist. Daher gilt für den Vorgang, genauso wie für Schwinden von Kapital, die Gleichung
dn=−n⋅K⋅dt und integriert n=n0⋅e− Kt , wobei n 0 die ursprüngliche Menge an Teilchen ist.
Der Zerfall ist durch nichts zu beeinflussen. Also gibt es keine Parameter. Die Gleichung
wird deshalb dazu verwendet, aus den Daten eines Experiments die Konstante K zu
bestimmen, die dann Zerfallskonstante λ (lambda) genannt wird. Sie ist für die jeweilige
radioaktive Substanz typisch.
Bei Jod 131 ist die Zerfallskonstante 0,000001 s−1 , das heißt die Teilchenmenge
vermindert sich in 1000000s auf den e-ten Teil.
Die Zeit, in der sich die Menge auf die Hälfte verringert hat, wird Halbwertszeit T h genannt.
Sie ist eine aussagekräftigere Variante der Zerfallskonstanten. Man erhält mit
und dann mit λ T h=ln 2 die Halbwertszeit T h =0,693/ λ
Für Jod 131 ist T h =
n0
−λT
=n 0⋅e
2
h
0,693
=693000s=8,02 d , also etwa 8 Tage.
10−6 s−1
Luftdruck und Höhe
Bei einer Flüssigkeitssäule nimmt der Druck mit zunehmender Höhe linear ab, und zwar
weil das spezifische Gewicht der Flüssigkeit γ konstant ist. Es gilt die einfache Beziehung
p= γ⋅h .
Bei Gasen, also auch bei Luft, ist das spezifische Gewicht vom Druck abhängig. Es wird mit
zunehmender Höhe kleiner. Diesen Verlauf kann man daher zunächst nur differentiell
angegeben, und zwar so: dp=−γ⋅dh
Bei konstanter Temperatur ist das Produkt aus Volumen V und Druck p eine Konstante
(Boyle-Mariottesches Gesetz). Also gilt für eine Ausgangshöhe 0 und eine beliebige andere:
p0⋅V 0 = p⋅V Weil Volumen und spezifisches Gewicht in umgekehrt proportionalem
Zusammenhang stehen, gilt: p0⋅γ = p⋅γ 0 und umgestellt γ=
p⋅γ 0
p0
Das spezifische Gewicht oben eingesetzt, ergibt die Differentialgleichung dp=− p
−
der bereits bekannten Form. Die Lösungsfunktion ist p= p ⋅e
0
γ0
h
p0
Die nach h umgestellte Formel, also zum Berechnen der Höhe, lautet:
γ0
dh in
p0
p0
p
h=− γ ⋅ln
0
p0
Das Beispiel zeigt, dass es nicht immer die Zeit ist, die als unabhängig Veränderliche im
Exponent der e-Funktion auftritt.
7