Kernstrahlung 7

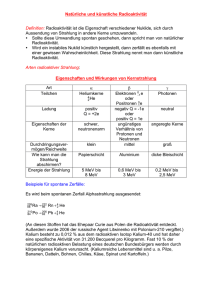
GRUNDPRAKTIKUM PHYSIK
KERNPHYSIKPROJEKT
KAY BERGEMANN, BJØRN-ERIK BRANDT, ROBERT FLASSIG,
MARCEL KAPPEL, MATTHIAS MÜLLER UND ANDREAS SCHULZE
Betreuer: Herr Dr. Schmidt.
1
Inhaltsverzeichnis
1. Strahlungsarten
1.1. α - Strahlen
1.2. β-Strahlen
1.3. γ-Strahlen
2. Detektoren
2.1. Der Szintillations-Detektor
2.2. Der Halbleiter-Detektor
2.3. Das Geiger-Müller-Zählrohr
3. α - Strahlung
3.1. α - Spektrum
4. β - Strahlung
4.1. β - Spektrum mit Hilfe eines Magnetfeldes
4.2. Absorption von β-Strahlung
4.3. β - Spektrum Kr 85
4.4. Beta-Rückstreuung
4.5. Halbwertszeit von Na - 22 (β − - Strahler)
5. γ - Strahlung
5.1. Prinzip der Abschwächung von γ-Strahlen
5.2. γ - Spektrum Cs 137
5.3. γ - Spektrum Co 60
2
2
3
3
4
4
4
5
5
5
10
10
14
16
19
21
23
23
26
30
1. Strahlungsarten
1.1. α - Strahlen.
α - Strahlung tritt beim radioaktiven Zerfall - vorwiegend aber bei natürlichen Nukliden auf und besteht aus α - Teilchen. Diese sind Heliumkerne (42 He), die zwei Protonen und zwei
Neutronen enthalten. Im einzelnen passiert folgendes beim α - Zerfall:
A
Zν
4
−→A−4
Z−2 ν + 2 He
Bei der Emission von Heliumkernen wandeln sich Atomkerne in andere Atomkerne, mit einer
um zwei kleineren Kernladungszahl und einer um 4 kleineren Massenzahl, um. Da die Bindungsenergie der ausgesandten α - Teilchen ungewöhnlich hoch ist (28,3 MeV) und sie weder
Spin noch magnetisches Moment besitzen, sind diese Kerne außerordentlich stabil.
Das Heliumkerne überhaupt emittiert werden kann zur Zeit nur mit Hilfe der Quantenmechanik erklärt werden. Nach der klassischen Physik gilt für die Gesamtenergie Eges = Epot + Ekin .
Danach könnte das α - Teilchen nur dann aus dem Wirkungsbereich der Kernkräfte gelangen,
wenn seine Gesamtenergie wenigstens so groß wie der größte Wert der potentiellen Energie wird.
Diese Energie müsste das emittierte Teilchen dann aber auch als kinetische Energie besitzen,
was nicht der Fall ist (Abb. 1). Offenbar gelangen aber Teilchen auf die andere Seite des Potentialwalls, ohne dass ihre potentielle Energie die dazwischen liegende Werte annimmt. Diese
Erscheinung bezeichnet man als Tunneleffekt. Die α - Teilchen durchtunneln“ den Potential”
wall (Abb. 1). Mit Hilfe der klassischen Physik ist dies nicht zu erklären.
2
Abbildung 1. Potential eines Atomkerns in Abhängigkeit des Abstandes zum
Mittelpunkt (aus Joachim Grehn, Metzler Physik / Zweite Auflage (Seite 492))
In der Quantenmechanik ist die Aufenthaltswahrscheinlichkeit der α - Teilchen proportional
zum Quadrat der Wellenfunktion |ψ|2 . Demnach ist die Wahrscheinlichkeit ein Heliumkern außerhalb des Potentialwalls zu finden nicht Null. Diese Wahrscheinlichkeit ist natürlich abhängig
von der Höhe und der Dicke des Walls. Also haben die Potentialwälle von α - Strahler günstige“
”
Bedingung, um Heliumkerne zu emittieren.
1.2. β-Strahlen.
Beim radioaktiven Zerfall kann es weiterhin dazu kommen, dass sich die beiden Nukleonensorten in einander umwandeln. Das Neutron kann in ein Proton und das Proton in ein
Neutron umgewandelt werden. Dabei werden aus Gründen der Erhaltung der elektrischen
Ladung noch weitere Teilchen vom Kern emittiert. Zum einen Elektronen-Neutrinos (ve ) oder
Elektronen-Antineutrinos (v e ) und zum anderen Elektronen (β − Teilchen) oder Positronen
(β + Teilchen). Im Einzelnen laufen die Umwandlungen wie folgt ab:
1
0n
1
1p
→11 p + e(β − ) + ν e
→10 n + e(β + ) + νe
In beiden Fällen bleibt die Nukleonenzahl erhalten. Nur die Kernladungszahl ändert sich: Beim
β − Prozess nimmt sie um eine Einheit zu, beim β + Prozess dagegen um eine Einheit ab. Abgesehen von der Ladung besitzen Elektronen und Positronen absolut identische Eigenschaften.
Ihre Reichweite ist größer als bei α-Teilchen und liegt bei etwa 50 cm. Das Durchdringungsvermögen ist dementsprechend gering. Durch eine recht geringe Masse von me = 9, 11 · 10− 31
kg kann es bei Kollisionen mit anderen Teilchen zu großer Streuung um hohe Winkel kommen.
Damit es zur Bildung von β + -Teilchen kommt, muss das neutrale Ausgangsatom gegenüber
dem neutralen Folgeatom einen Energieüberschuss von E = 2 · m · c2 = 1, 022 MeV besitzen.
Für die Entstehung eines β + -Teilchens muss die bei der Kernumwandlung frei werdende Energie
dagegen etwas geringer sein. Gute β-Strahler sind z.B. Krypton-85 oder Strontium-90.
1.3. γ-Strahlen.
Bei der Kernumwandlung kann eine energiereiche elektromagnetische Strahlung auftreten,
die sog. Gammastrahlung. Abgesehen von der Art der Entstehung ist sie identisch mit
Röntgenstrahlung.
Die γ-Quanten bewegen sich mit einer konstanten Geschwindigkeit, der Vakuumlichtgeschwindigkeit. Diese entstehen dadurch, dass der Atomkern nach Ausschleudern eines Alpha3
oder Betateilchens noch vorhandene überschüssige Energie in Form eines oder mehrerer
Gammaquanten abgibt.
Durch den γ-Zerfall ändert sich der Energieinhalt des Kerns, nicht jedoch dessen Kernladungsoder Massenzahl.
Beispiel:
∗
137
56 Ba
→
137
56 Ba
+γ
γ-Teilchen sind weder elektrisch noch magnetisch ablenkbar und haben ein sehr gutes Durchdringungsvermögen von Materie. Dafür sind sie kaum in der Lage, andere Atome zu ionisieren.
2. Detektoren
2.1. Der Szintillations-Detektor.
Teilchen, die mit einem Szintillations-Zähler analysiert werden, treffen als erstes auf den
Szintillator, welcher häufig aus einem Natrium-Iodid-Kristall besteht. Dort verliert ein
Teilchen Energie, indem es in dem Kristall Elektronen in energetisch höhere Energiezustände
hebt. Diese Anregungen werden durch Emission von Photonen wieder abgebaut. Ein Teil der
Photonen gelangt nun durch einen Lichtleiter auf eine Fotokathode und löst dort Elektronen
aus. Diese Elektronen werden in einer Kette von Elektroden, den sog. Dynoden, beschleunigt,
sodass ein Elektron auf jeder Dynode 2-5 weitere Elektronen auslöst (Sekundärelektronen). So
kann man Gesamtverstärkungen bis 109 erreichen. Eine geringe Anzahl Photonen erzeugt also
am Ausgang des sogenannten Multipliers einen messbaren Impuls. Die Höhe des Impulses ist
proportional zur Energie, die das einfallende Teilchen im Szintillator abgegeben hat. Dabei
kann man verschiedene Messmethoden anwenden:
Einkanalimpulshöhenanalyse:
Hierbei tastet man den Energiebereich mit einem sog. Kanalfenster ab. Alle Teilchen,
deren Energie in diesem Kanalfenster liegen, werden vom Szintillationsdetektor gewertet. Alle anderen Teilchen die mit ihrer Energie nicht in dem Kanalfenster liegen werden
nicht mitgezählt. Das gesamte Energiespektrum einer Strahlenquelle erhält man, indem
man das Kanalfenster einfach durchpegelt“ - soll heißen, dass man einfach die Ener”
giewerte der beiden Diskriminatoren von 0 an erhöht. Dabei werden je nach Hersteller
verschiedene Skalen benutzt. Diese Methode liefert ein differentielles Spektrum (Bsp. s.
Abs. 5.2) bei Verwendung eines Kanalfensters. Benutzt man nur einen Diskriminator,
so entsteht ein integrales Spektrum (Bsp. s. Abs. 5.2).
Mehrkanalimpulshöhenanalyse:
Analoge Methode wie die Einkanalimpulshöhenanalyse. Diese benutzt mehreren Kanalfenstern mit dem Vorteil, dass nicht mehr durchgepegelt werden muss.
Mit Hilfe des Szintillations-Detektors werden in erster Linie γ− und β−Teilchen untersucht.
Je nach Strahlungsart, werden unterschiedliche Szintillatoren verwendet.
2.2. Der Halbleiter-Detektor.
Der Halbleiter-Detektor besitzt ein wesentlich höheres Auflösungsvermögen als der
Szintillations-Zähler. Die einfallende Strahlung wird hier durch Erzeugung von Ladungen in
der an Ladungsträgern völlig verarmten Sperrschicht registriert. Auch beim Anlegen einer
Spannung ist diese nicht allzu groß. Eine Vergrößerung der Schicht wird oftmals durch Eindiffundieren von Lithium N -leitendes mit Bor dotiertem Germanium erreicht.
Die in der Sperrschicht erzeugten Ladungspaare fließen im elektrischen Feld zu Elektroden ab.
Der so entstehende Spannungsimpuls wird ähnlich wie beim Szintillator verarbeitet und so
4
messbar gemacht. Thermische Anregungen können dabei unerwünschte Ströme erzeugen.
Der Halbleiter-Detektor wird hauptsächlich zur Messung von α− und β−Strahlung verwendet.
2.3. Das Geiger-Müller-Zählrohr.
Das Zählrohr ist ein Gerät, das die durch einfallende Elementarteilchen mittels Stoßionisation
erzeugte Ladungsträgerlawine in zählbare Stromimpulse umwandelt.
Eindringende geladene Teilchen ionisieren eine bestimmte Anzahl der Atome des Füllgases. Die
durch Ionisation entstandenen Elektronen und Ionen werden im elektrischen Feld beschleunigt,
besonders die Elektronen stoßen mit weiteren Gasatomen zusammen und ionisieren auch diese
(Stoßionisation). Sie lösen damit eine Ladungsträgerlawine aus, die im Zählrohrkreis einen
Stromstoß erzeugt. Der kurzzeitige Stromstoß ergibt am Aussenwiderstand des Zählrohres einen
Spannungsstoß, der mittels des anschließenden Verstärkers als knackendes Geräusch hörbar
gemacht werden kann.
3. α - Strahlung
3.1. α - Spektrum.
3.1.1. Einführung.
Die α - Spektrometrie ist die experimentelle Technik zur Bestimmung des α - Spektrums. Sie
dient heute vor allem zur Untersuchung der bei Kernreaktionen emittierten Teilchen. In unserem Fall wurde das Spektrum mit Hilfe eines Halbleiterdetektors aufgenommen.
Die maximale Reichweite von α - Teilchen in Luft unter normalen Luftdruck liegt unter 10
cm. Wird der Luftdruck verringert, so steigt die Reichweite an (die auftretenden Effekte werden später erklärt). Unsere Aufgabe lag nun darin das α - Spektrum von Americium 241 in
Abhängigkeit vom Luftdruck zu untersuchen. Doch bevor wir messen konnten, mussten wir die
x-Achse (in unserem Fall die Energie der Teilchen in MeV) neu skalieren.
3.1.2. Skalierung der x-Achse.
Da unsere Messapparatur zwar das Intensitätmaximum gut wiedergab, aber die x-Werte
(Energie der α - Teilchen in MeV) nicht übernahm, waren wir gezwungen, unsere x-Achse
neu zu skalieren. Dazu benutzten wir zwei Präparate von Americium - 241. Das eine mit 370
kBq, also einer hohen Radioaktivität und das andere mit 3,7 kBq, also einer relativ kleinen
Radioaktivität. Mit dem Präparat der höheren Aktivität wurde die eigentliche Messung in
unserem Experiment gemacht, da durch den höheren Ausstoß der α - Teilchen eine genauere
Messung möglich ist. Zum Schutz vor der Probe wurde vor dem radioaktiven Material eine
dünne Platin-Goldschicht angebracht. Dadurch werden aber die Heliumkerne abgebremst - sie
verlieren kinetische Energie.
Das zweite Präparat mit der nicht so hohen Aktivität hat allerdings keine solche Folie, was
erhöhte Vorsicht im Umgang mit der Probe nach sich zog. Dadurch waren wir aber in der
Lage, die Energie der Teilchen ungebremst zu messen.
Um weiterhin möglichst genaue Werte zu bekommen, wurde die Kammer in der sich die Probe
befand evakuiert. Wir erreichten einen minimalen Druck von 16 mbar. Bei 5,484 MeV konnten
wir das Intensitätsmaximum des α - Spektrums der Probe mit der geringeren Aktivität
annehmen (→ Literatur). Im selben Abstand zum Detektor wie die erste Probe wurde nun das
aktivere Präparat in die Apparatur eingesetzt. Das Spektrum ist aufgenommen worden und
wird im folgenden nun mit dem ersten Spektrum verglichen:
Daraus ergibt sich ein Intensitätmaximum der aktiveren Probe bei 4,5 MeV. Durch die
Platin-Goldfolie werden die α - Teilchen wegen der Wechselwirkungen mit der Folie um
ungefähr 1 MeV abgebremst.
5
Häufigkeitsverteilung
unbeschichtete Probe
beschichtete Probe
5.484 MeV
PSfrag replacements
/
0
1
2
3
Energie / MeV
4
5
6
Abbildung 2. Skalierung mit Hilfe der unbeschichteten Probe Americium - 241
3.1.3. α - Spektrum bei unterschiedlichen Luftdruck.
Mit der vorhergehenden Skalierung ist es nun möglich das α - Spektrum in Abhängigkeit des
Luftdrucks zu messen. Hierbei wird die zu untersuchende Probe immer im gleichen Abstand
zum Halbleiterdetektor gelassen (In unserem Fall 2 cm). Nun wird die Kammer, in welches
sich das Präparat befindet, so weit wie möglich evakuiert, um den Minimaldruck zu erreichen
(16 mBar). Dort wird die erste Kurve aufgenommen. Jetzt wird schrittweise wieder Luft in
die Kammer gelassen und bei bestimmten Luftdrücken werden weitere Kurven aufgenommen.
Dieses Vorgehen ergibt diese Graphik:
Häufigkeitsverteilung
16 mbar
150 mbar
300 mbar
451 mbar
600 mbar
750 mbar
901 mbar
1026 mbar
1
2
3
Energie / MeV
4
5
6
Abbildung 3. Abhängigkeit des α - Spektrums vom Luftdruck
Man erkennt, dass die Kurven mit zunehmenden Druck kleiner und breiter werden und nach
links abwandern.
Kleiner werden die Kurven, weil durch Streuung an den Luftmolekülen die kinetischen Energien
6
der Teilchen sich statistisch verteilen. Dadurch werden die Graphen natürlich auch breiter.
Ein weiterer Effekt ist die Stoß-Ionisation der Luftmoleküle mit den α - Teilchen. Deshalb
verlieren die ausgesandten Heliumkerne bei jedem Stoß kinetische Energie - die Kurve wandert
nach links. Da aber nun manche α - Teilchen mehr Luftmoleküle treffen als andere, gehen die
Energien der Teilchen wieder auseinander - die Kurve wird wieder breiter.
Vergleicht man die folgenden Kurven miteinander:
Häufigkeitverteilung
16 mbar
1026 mbar
1
2
3
Energie / MeV
4
5
6
Abbildung 4. Symmetrische und asymmetrische Kurve
so erkennt man, dass die Kurve, die bei niedrigen Druck aufgenommen wurde, leicht asymmetrisch ist. Das heißt vom Intensitätsmaximum aus gesehen gibt es durchschnittlich weniger
schnelle Teilchen als langsamere. Vergleicht man mit dem Graphen, der bei Normaldruck
gemacht wurde, so gibt es dort im Gegensatz zur ersten Kurve vom Intensitätsmaximum aus
gesehen mehr schnellere Teilchen. Das kommt von einer weiteren Wechselwirkung mit den
Luftmolekülen. Diese schwingen nämlich schnell hin und her und dabei stoßen sie hin und
wieder α - Teilchen so an, dass diese beschleunigt werden.
Im Allgemeinen kann man sagen: Je mehr Wechselwirkungen der α - Teilchen mit den Luftmolekülen vorhanden sind, umso kleiner und breiter wird der Graph des Intensitätsmaximums
des α - Spektrums. Außerdem wandert dieser weiter nach links im Diagramm.
Dieser Versuch kann auch dazu genutzt, werden die Reichweite von α - Teilchen zu untersuchen.
Würde man nämlich den Abstand zwischen Präparat und Detektor verändern, käme es zu
gravierenden Ungenauigkeiten aufgrund des divergierenden Strahls der radioaktiven Probe. Es
würden mit wachsenden Abstand immer weniger α - Teilchen den Detektor treffen - sie würden
einfach vorbei fliegen. Also lässt man die Distanz gleich und verändert einfach den Luftdruck.
Wäre der Luftdruck so hoch, das in den zwei Zentimetern zwischen Präparat und Detektor
so viele Luftmoleküle wären wie bei Normaldruck und zehn Zentimeter Abstand, so käme
auch kein Signal am Halbleiterdetektor mehr an. Für diesen Aspekt des Versuchs war unsere
Apparatur aber nicht ausgelegt. So belassen wir es bei dieser theoretischen Behandlung.
7
3.1.4. Feinstruktur des α - Spektrums.
Für diesen Versuch benutzten wir das Präparat ohne Schutzfolie, da mit Folie eine genaue
Auflösung nicht möglich ist.
Das Feinspektrum von Americium - 241 besteht aus fünf Übergangswahrscheinlichkeiten:
Nr. Energie in MeV Übergangswahrscheinlichkeit
1
5,387
1,6 %
2
5,442
12,5 %
3
5,484
85,2 %
4
5,511
0,2 %
5
5,543
0,34 %
Das sieht dann folgendermaßen aus:
Abbildung 5. Feinstruktur des α - Spektrums (aus Joachim Grehn, Metzler
Physik / Zweite Auflage (Seite 474))
Diese fünf Übergänge kommen wie folgt zustande:
Schwache Linien etwas geringerer Energie rühren daher, dass der Endkern angeregt ist. Diese
überschüssige Energie beim Endkern fehlt natürlich dem α - Teilchen. Zusätzlich ist dieser α
- Zerfall von einer schwachen γ - Strahlung begleitet, die von der Abregung des Endkernes
herrührt.
Ist der durch β - Zerfall entstandene Ausgangskern schon angeregt, dann sind, wie in Abb.
4 sichtbar, auch Feinstrukturlinien höherer Energie möglich, da der angeregte Kern diese
überschüssige Energie an die α - Teilchen abgibt. Der häufigste Übergang (85,2 %) ist aber
von nicht angeregten Anfangskern zu nicht angeregten Endkern.
Um die Feinstruktur so genau wie möglich aufzunehmen, schoben wir die Probe so dicht wie
möglich an den Detektor heran, ohne diesen aber zu berühren. Zusätzlich wurde die Kammer
wieder evakuiert (16 mbar). Folgende Feinstrukturspektren kamen dabei heraus:
8
Häufigkeitverteilung
PSfrag replacements
5.44 MeV
5.44 MeV
↓
↓
5,45
5,5
5.44 MeV
↓
5,45
5,5
5,45
5,5
Energie in MeV
Abbildung 6. Drei Feinstrukturaufnahmen mit unterschiedlichen Parametern
Wie man den Abbildungen entnehmen kann, war leider nur eine sichere Zuordnung für die
Übergänge 1 und 2 (5,442 bzw. 5,484 MeV) möglich. Die anderen Übergänge sind von der
Wahrscheinlichkeit auch ziemlich gering (1,6 %; 0,2 %; 0,2 %). Eine nicht komplett evakuierte Kammer mit 1,56 % Luftmolekülen im Vergleich zum Normaldruck verschlechtern die
Versuchsbedingungen noch zusätzlich.
9
4. β - Strahlung
4.1. β - Spektrum mit Hilfe eines Magnetfeldes.
In diesem Versuch wird das Energiespektrum verschiedener Beta-Strahler mit Hilfe eines von
einem Magnetfeld durchsetzten Beta-Spektroskop untersucht. Mit dem Beta-Spektroskop wird
die Geschwindigkeit von Beta-Teilchen gemessen und daraus deren Energie berechnet. Als
Strahlungsquellen wurden im Folgenden sowohl Krypton (Kr-85) als auch Strontium (Sr-90)
verwendet. Beide Präparate sind gute Beta-Strahler.
4.1.1. Versuchsanordnung.
Das Beta-Spektroskop besteht aus einer runden Flachkammer, deren dicke zylindrische Wand
aus nicht magnetisierbarem Material besteht. Boden und Deckel werden von zwei flachen
Polschuhen gebildet. In die Kammer können sowohl Strahlungsquellen als auch ein Geigermüllerzählrohr eingeführt werden. Das gesamte Spektroskop kann so auf eine Magnetspule
gesteckt werden, so dass sein Inneres von einem Magnetfeld durchsetzt wird. In die Kammer
eintretende Elektronen werden auf Grund des herrschenden Magnetfeldes auf eine Kreisbahn
gezwungen. Aus diesem Grund ist auf dem Boden ein System aus Blenden angeordnet, welche
die von der vorgegebenen Kreisbahn abweichenden Beta-Teilchen ausblendet. Die Teilchen
bewegen sich anschließend ins Innere des Geigermüllerzählrohres, wo sie auf Ihre Anzahl hin
überprüft werden können.
4.1.2. Theorie und Formeln.
Treten die Elektronen in das Spektroskop ein und treffen auf das Magnetfeld, so werden
sie auf eine Kreisbahn gelenkt. Die Elektronen besitzen jedoch unterschiedliche Energien.
Teilchen mit hoher kinetischer Energie benötigen auch eine stärkere Magnetfeldstärke B um
auf die Bahn gebracht zu werden, die sie zur Analyse in das Geigermüllerzählrohr lenkt. Je
nach Magnetfeldstärke, die durch eine an der Spule anliegenden Spannung reguliert werden
kann, werden also unterschiedliche Elektronenenergien untersucht. Durch Variation des
Magnetfeldes kann somit ein komplettes Energiespektrum der Beta-Teilchen erfasst werden,
um so Rückschlüsse auf Ihre kinetische Energie ziehen zu können.
Bei der Umwandlung der Nukleonen im Atomkern werden außer den Beta-Teilchen aber
auch noch Neutrinos freigesetzt. Die Umwandlungsenergie Q verteilt sich demnach nach dem
Wahrscheinlichkeitsgesetz gleichermaßen auf Betateilchen und Elektronenneutrino.
(1)
Q = E β + E νe
Das kontinuierliche Energiespektrum gibt dabei Werte von Eβ = 0 bis Eβ = Eβmax (Eνe = 0)
an. Entscheidend ist dabei der Wert, für den Eβ ein Maximum annimmt. An diesem Punkt
besitzt, wie oben beschrieben, auch die Magnetfeldstärke B Ihr Maximum.
Doch auch bei der stärksten Magnetfeldablenkung werden am Geigermüllerzählrohr noch Teilchen registriert. Bmax entspricht also nicht automatisch einer Impulsrate von Null. Dies liegt
zum einen an einer konstanten thermischen Strahlung und teilweise auch an einer gewissen
γ-Strahlung, die selbst bei Beta-Strahlern nicht absolut Null ist. Diese Hintergrundstrahlung
muss durch Subtraktion von der Gesamtstrahlung bei der Auswertung berücksichtigt werden.
Auf der Kreisbahn der Elektronen sind die Lorentzkraft, hervorgerufen durch das magnetische
Querfeld und die Zentrifugalkraft im Gleichgewicht.
(2)
e·v·B =
10
m · v2
r
Für den Impuls folgt somit
(3)
p=m·v =e·B·r
bzw. für relativistische Teilchen
ε2
= p2 + m20 · c2
c2
Die Gesamtenergie ε setzt sich weiterhin aus kinetischer Energie εkin und Ruheenergie m0 · c2
zusammen:
(4)
ε = εkin + m0 · c2
(5)
Somit folgt für die kinetische Energie
q
(6)
εkin = (e · B · r · c)2 + m20 · c4 − m0 · c2
Dies ist letztendlich die gesuchte Beziehung zwischen der Teilchenenergie und der Kraftflussdichte. Der Radius r bezeichnet dabei den Radius der Teilkreisbahn, auf der sich die
Beta-Teilchen durch das Spektroskop bewegen. Er wurde vom Hersteller mit r = 50 mm
angegeben.
4.1.3. Versuchsdurchführung.
Aufzeichnung der Kennlinie des Zählrohres
Als erstes wird die Kennlinie des Geigermüllerzählrohres aufgezeichnet. Dazu wird die Spannung des an das Zählrohr angeschlossenen Impulsratenmessers von ca. 200 V auf 600 V erhöht.
Die Impulse, die dabei pro Sekunde vom Zählrohr registriert werden, werden gleichzeitig
aufgenommen. Die mit Hilfe des Computerprogrammes DASYLAB vorgenommene graphische
Auswertung zeigt, dass sich die Impulsrate ab einer Spannung von ca. 300V nicht weiter
erhöht und erst wieder bei etwa 550V anfängt zu steigen. In diesem Bereich befindet sich
ein Plateau. Um das Beta-Spektrum anschließend möglichst fehlerfrei zu vermessen, ist es
von Nöten diesen Bereich der Kennlinie zu ermitteln. Denn auch wenn die Betriebsspannung
während einer Messung einmal um einen geringen Wert schwanken sollte, so hätte dies keinerlei
Auswirkungen auf die Impulsrate, da diese im Bereich des Plateaus konstant ist. Die konstante
Betriebsspannung für die Vermessung des Energiespektrums wurde auf 425V festgelegt.
Imp/s
15
10
5
0
200
300
400
Spannung / V
500
Abbildung 7. Detektorkennlinie
11
600
Mit Hilfe des an die Magnetspule angeschlossenen Labornetzgerätes wird das Magnetfeld
jeweils um 5 mT erhöht und gleichzeitig die Impulsrate gemessen. Die graphische Auswertung
erfolgt wiederum mit DASYLAB. Nacheinander wurden die Präparate Kr-85 und Sr-90 auf
Ihre Teilchenenergien hin überprüft. In der Tat erhält man in beiden Fällen ein kontinuierliches
Energiespektrum.
40
15
Spektrum Sr-90
Spektrum Kr-85
30
Imp/s
Imp/s
10
20
5
10
0
0
50
100
0
150
B / mT
0
50
100
150 200
B / mT
250
300
Abbildung 8. Energiespektren von Kr-85 sowie Sr-90
Wie zu erwarten war, bildet sich jeweils ein Impulsratenmaximum aus und später eine
asymptotische Angleichung der Kurve an einen bestimmten Impulsratenwert; dem Wert der
Hintergrundstrahlung. In diesem Bereich ist das Maximum der Magnetfeldstärke zu suchen.
4.1.4. Auswertung des Beta-Spektrums.
Als erstes lässt sich durch einfache Betrachtung des Spektrums schnell erkennen, ob es sich
bei den ausgesandten Beta-Teilchen um Elektronen oder Positronen handelt. Auf Grund
der zwischen positivem Atomkern und Beta-Teilchen herrschenden Coulombkraft, werden
Elektronen beim Verlassen des Kerns ein wenig abgebremst, Positronen dagegen werden
beschleunigt. Dementsprechend gäbe es im Fall von Elektronen mehr Teilchen mit geringerer
Energie bzw. mehr Teilchen bei einer geringen herrschenden magnetischen Feldstärke. Und
genau dies ist hier der Fall. Auch wenn es nicht möglich war die Feldstärke B völlig auf Null
zu regeln, ist eine Tendenz im unteren Feldstärkenbereich deutlich erkennbar. Sowohl Kr-85
als auch Sr-90 senden Elektronen aus.
Um nun Rückschlüsse auf die maximale kinetische Energie der Elektronen zu ziehen, ist
es notwendig, Bmax zu bestimmen. Wie bereits erwähnt muss man hierbei zunächst die
Hintergrundstrahlung abziehen. Selbige erhält man einfach durch eine zusätzliche Messung bei
abgeschaltetem Magnetfeld. Die Elektronen werden so nicht abgelenkt und vom Zählrohr auch
nicht registriert. Was somit am Zählrohr ankommt, sind sowohl die thermische als auch die
γ-Strahlung, die zusammen die störende Hintergrundstrahlung bilden. Beide Teilchenformen
12
sind nicht geladen und treffen stets durch Streuung auf das Zählrohr. Da der γ-Anteil von
Kr-85 und Sr-90 jeweils unterschiedlich ist, unterscheidet sich auch die gemessene Hintergrundstrahlung in beiden Fällen etwas. Beim Krypton ergab sich eine abzuziehende Teilchenanzahl
von N = 0,62 beim Strontium dagegen betrug N = 0,75.
Durch Anwendung von Gl. 6 erhält man folgende Werte:
Bmax
Ekin
Ekin (Literatur)
Kr-85 119 mT 1,35 MeV
672 keV
Sr-90 265 mT 3,49 MeV
2,27 MeV
Wie man leider erkennen kann, weichen die errechneten Werte beide Male erheblich von
den angebenden Literaturwerten ab. Vermutungen, dass diese Diskrepanzen an einer falschen
Hersteller-Angabe des Kreisbahnradius r liegen, sollten sich bestätigen. Löst man Gleichung 6
nämlich nach r auf und verwendet anstatt der Messwerte die Literaturwerte der maximalen
kinetischen Energie der Elektronen, so erhält man mit
(7)
p
(ELit + m0 · c2 )2 − m20 · c4
r=
e·B ·c
bei Kr-85 einen Radius von r = 2,98 cm und bei Sr-90 einen Radius von r = 3,45 cm.
Die Herstellerangabe von 5 cm scheint insofern wie vermutet völlig unbrauchbar zu sein.
Leider hatte diese Tatsache zur Folge, dass während des gesamten Praktikums, mit Hilfe der
Magnetfeld-Methode, keinerlei befriedigende Energiewerte bestimmt werden konnten, da hierzu
der exakte Kreisbahnradius benötigt wird. Mit Hilfe weiterer Präparate hätte der tatsächliche
Radius durch Rückrechnung noch genauer bestimmt werden können um folgende Messungen
zufriedenstellender zu machen. Doch Versuche mit z.B. Cobalt, das hauptsächlich als γ-Strahler
verwendet wird, ergaben keine befriedigenden Ergebnisse, da der Anteil der ausgesandten
Beta-Strahlung zu gering war und teilweise sogar im Bereich der Hintergrundstrahlung lag.
4.1.5. Weitere Fehlerquellen.
Ein weiterer Grund für die ungenauen Messungen könnte auf der Tatsache beruhen,
dass es in der Regel recht schwer war den Wert Bmax zu ermitteln. Theoretisch ist er dann
erreicht, wenn die Impulsrate den Wert der Hintergrundstrahlung angenommen hat. Doch
erstens lag die Impulsrate am Ende immer noch etwas über der Hintergrundstrahlung - was
zum einen auch daran liegt, dass auch die Hintergrundstrahlung nur als Mittelwert errechnet
wurde - und zum anderen schwankt die Impulsrate auch im unteren Bereich immer noch
so stark, dass eine genaue Gleichsetzung sehr schwer ist. Weiterhin basiert die gesamte
Werteaufzeichnung nur auf einer Einkanal-Auswertung. Die Werte können somit generell
recht schwanken, da sie stets einer gewissen statistischen Unsicherheit obliegen. Ein am Ende
aufgezeichnetes Strontium-Energiespektrum, das mit einem Vielkanaler gewonnen wurde,
ergab auch in der Tat besser auszuwertende Messdaten.
13
4.2. Absorption von β-Strahlung.
4.2.1. Einführung.
Beim Durchgang von β-Strahlung durch ein Metall oder andere Materialien wird es absorbiert.
Für geringe Schichtdicken gilt für β-Strahlung näherungsweise das Absorptionsgesetz:
(8)
µ
ϕ(d) = ϕ(0)e− ρ d
mit d = ρx die Flächenmasse , µ/ρ Massen-Absorptionskoeffizient.
Die Elektronen ( bei β − -Strahlung ) werden außerdem aufgrund der Coulombwechselwirkung
in Metallen sowohl an den frei beweglichen Elektronen, als auch an der Elektronenhülle
der Atomrümpfe gestreut. Durch mehrfache Streuung wird der zurückgelegte Weg der
β-Strahlung größer als die eigentliche Schichtdicke. Für größere Schichtdicken weicht die
Absorptionskurve daher vom Absorptionsgesetz ab. Die β-Strahlung hat in Materialien eine
endliche maximale Reichweite Rmax , die der Reichweite der energiereichsten Teilchen entspricht.
4.2.2. Durchführung.
Es soll die Absorptionskurve für die β-Strahlung von Krypton 85 aufgenommen werden. Als
Detektor wird ein Szintillationsdetektor verwendet, der speziell β-Strahlung messen soll, aber
natürlich auch γ-Strahlung registriert.
Zu Beginn wird die Kennlinie des Detektors aufgenommen.
Aus dieser ergibt sich eine Arbeitsspannung von etwa 1000 V, die auf dem Arbeitsplateau
liegt. Es werden nacheinander Aluminiumplätchen unterschiedlicher Dicke, also unterschiedlicher Flächenmasse zwischen Strahler und Detektor gebracht, und die Impulse am Detektor
gemessen. Zur Flächenmasse des Schicht muss noch die Flächenmasse der Luftschicht und des
Detektorfensters (d = 6 mg/cm2 )hinzu addiert werden. Bei der ersten Messung ergibt sich in
halblogarithmischer Darstellung Abbildung 2.
14
Dabei ist erkennbar, dass für geringe Schichtdicken exponentieller Abfall (linear in logarithmischer Darstellung) auftritt. Für den exponentiellen Teil der Kurve ergibt sich ein
Massen-Absorptionskoeffizient von 3,0983 m2 /kg. Aus der Näherungsformel
(9)
µ
−1,43
= 1, 7 · Emax
ρ
erhält man eine Maximalenergie der β-Strahlung von 0,657 MeV. Dies stimmt bereits sehr gut
mit dem Literaturwert von 0,672 MeV überein.
Zudem sieht man, dass die Impulsrate ab einer Flächenmasse zwischen 2 und 3 einen konstanten Wert annimmt. Diese Impulse werden durch γ-Strahlung vom Strahler sowie der Hintergrundstrahlung und Bremsstrahlung der β-Teilchen hervorgerufen. Die β-Strahlung ist dort
vollständig absorbiert. Diese Flächenmasse ρRmax ist die maximale Massen-Reichweite von βStrahlung in Aluminium.
Aus dieser Reichweite lässt sich die Maximalenergie der β-Strahlung berechnen, wobei für ein
Intervall der Maximalenergie von 0,15 MeV bis 0,8 MeV die Formel nach Glendelin benutzt
wird
(10)
ρRmax = 4, 07 · Eβ1,38
.
max
Mit Eβmax = 0, 672 MeV ergibt sich ρRmax = 2, 35 kg/m2 (in Abbildung als Senkrechte eingezeichnet). Diese Massen-Reichweite stimmt gut mit der Messung überein, es lässt sich aus der
Messung allerdings kein genauer Wert ermitteln.
In einer zweiten Messung wurde ρRmax genauer ausgemessen (Abbildung 3). Bei den unteren Werten im Diagramm wurde der γ-Hintergrund abgezogen, entspricht also nur noch der
β-Strahlung. Die Kurve nähert sich asymptotisch ρRmax (senkrechte Gerade). Daraus folgt
näherungsweise ρRmax = 2, 5 kg/m2 und damit
(11)
Eβ max = 0, 702 MeV.
Dies weicht um 4,5 % vom Literaturwert ab. Diese Abweichung ist nicht verwunderlich, da wegen der geringen Impulsrate nahe der maximalen Massen-Reichweite nur relativ wenige Impulse
gemessen werden können, wenn man nicht sehr lange Messzeiten in Kauf nehmen will. Somit
15
sind die wichtigsten Werte am ungenausten gemessen.
Nimmt man den Literaturwert für Eβ max = 0, 672 MeV, so folgt für die Reichweite der energiereichsten β-Teilchen mit ρRmax = 2, 35 kg/m2 und ρAl = 2702 kg/m3
Rmax = 0, 87 mm.
Die Maximalenergie Eβ max der β-Strahlung lässt sich mit dieser Methode recht zuverlässig
ermitteln. Um sie exakt zu messen eignet sie sich allerdings weniger, da die Impulsrate
nahe ρRmax möglichst genau gemessen werden müsste und die benutzten Formeln lediglich
empirische Näherungsformeln sind.
4.3. β - Spektrum Kr 85.
Der Versuchsaufbau ähnelt dem der Spektrumaufnahme des Cs 137 und des Co 60. Wir verwenden einen für β - Strahlung optimierten Szintillationskristall. Nachdem der Arbeitspunkt und
die Verstärkung festgelegt sind beginnen wir mit der Aufnahme. Dabei erproben wir zwei Verfahren der Einkanalimpulshöhenanalyse - differentielle und integrale Messung (s. Abs. 5.2.3).
Wir erhalten folgende differentielle und integrale Spektren:
16
Impulsrate
a)
300
250
200
150
100
50
0
0
20
40
0
20
40
60
80
100
60
80
100
Pegel / %
Impulsrate
b)
PSfrag replacements
3000
2500
2000
1500
1000
500
0
Pegel / %
Abbildung 9. β - Spektrum Kr 85: a) differentielle und b) integrale Verteilung
Auch an dieser Stellen wollen wir wie in Abschnitt 5.2.3 zeigen, dass beide Messungen (differentiel und integral) die gleichen Aussagen liefern. Betrachte dazu Abbildung 10. Integriert man
die differentiellen Messwerte, so erhält man das integrale Spektrum - nachdem das Vorzeichen
entsprechend vertauscht wurde.
3000
integral
differentiell
Impulsrate
2500
2000
1500
1000
PSfrag replacements
500
0
0
20
40
Pegel / %
60
Abbildung 10. Differentielles und integrales Spektrum des Kr 85
4.3.1. Energiebetrachtung. Aus dem differentiellem β - Spektrum können wir nun über einen
interessanten Umweg die Maximalenergie des β − - Teilchens bestimmen. Wir müssen eine
Möglichkeit finden, um den Maximalwert der asymptotische Annäherung der Messdaten zu
bestimmen. Dazu hat Fermi folgendes Auswerteverfahren entwickelt.
17
Plottet man die Funktion
(12)
f (E) =
s
p2
N
,
F (E)
so erhält man eine Gerade, welche die Abszisse bei E = Eβ − max = 672 keV schneiden
sollte. Dabei ist N die Anzahl der Impulse, p der Impuls des β − - Teilchen und F (E) der
energieabhängige Fermifaktor.
Impuls:
Den Impuls können wir aus der Energiebetrachtung berechnen:
E 2 = E02 + p2 c2
E = E0 + Ekin
Fermifaktor:
Den Energie und Ordnungszahl abhängigen Fermifaktor entnehmen wir einer Tabelle aus
[Landolt-Börnstein]1. Nach Interpolation erhalten wir folgende grafische Abhängigkeit
des Fermifaktors von der Energie für Kr 85:
30
(-8,7 E)
F(E) = 5,35 + 54,42 e
Fermifaktor F(E)
25
20
15
10
PSfrag replacements
Pegel / %
Impulsrate
5
0
0
0,2
0,4
Energie / MeV
0,6
0,8
Abbildung 11. Fermifaktor für Kr 85
Dabei haben wir den letzten Energiewert, der noch gerade über der Umgebungsstrahlung liegt
als Fixpunkt für die Eichung verwendet. Die Wahl des Fixpunktes für die Eichung muss sehr
gewissenhaft durchgeführt werden, da dieser das Endergebnis maßgeblich beeinflusst.
In Abbildung 12 habe wir die Regressionsgerade ab dem Energiewert von 0,19 Mev ausgerechnet. Diese liefert einen Maximalwert für die Energie des β - Teilchen von
(13)
Eβ − max = 0, 653 MeV
(vgl. Abs. 4.2.2).
Ein recht akzeptabler Wert, denn der wahre Energiewert liegt bei 0,672 MeV.
1Landolt-Börnstein:
Bd 1/4, Springer, 1969
18
3e+09
y(E) = 2, 92 · 109 − 4, 47 · 109 · E
2,5e+09
1,5e+09
f (E) =
q
N
p2 F (E)
2e+09
PSfrag replacements
1e+09
Eβ − max
5e+08
0
0
0,2
0,4
Energie / MeV
0,6
0,8
Abbildung 12. Fermiplot für Kr 85
4.4. Beta-Rückstreuung.
4.4.1. Einleitung. Trifft β-Strahlung auf ein Material, so wird sie an ihm durch elektromagnetische Wechselwirkung oder auch durch elastische Stöße mit Atomkernen (bzw. mit der Atomhülle
bei β + -Strahlung) gestreut. Dabei kann die Ablenkung so groß sein, dass die β-Teilchen direkt in
ihre Ausgangsrichtung zurückgeworfen werden. Wahrscheinlicher jedoch treten mehrere Wechselwirkungen auf, bei denen die sie dann entweder zurück gestreut oder vom Material absorbiert
bzw. transmittiert werden.
Bei diesem Experiment verwendeten wir einen Krypton-85-Strahler. Die von ihm abgegebene β − -Strahlung wurde dann von darüber befindlichen Platten unterschiedlicher Materialien
sowie diversen Aluminium-Folien reflektiert und mittels eines Geiger-Müller-Zählrohrs detektiert. Durch diesen Aufbau war es uns möglich, die Rückstreuung von Beta-Strahlung sowohl
in Abhängigkeit von der Ordnungszahl als auch in Abhängigkeit von der Schichtdicke bzw.
Flächenmasse zu untersuchen.
4.4.2. Rückstreuung in Abhängigkeit von der Schichtdicke. In diesem Teilversuch verwendeten
wir Aluminiumfolien als Rückstreumaterial. Durch Übereinanderschichten mehrerer Folien war
es uns möglich, die Schichtdicke in Schritten von 0, 018 mm zu erhöhen. Die Impulsraten wurden
jeweils dreimal aufgenommen und gemittelt, um statistische Schwankungen möglichst auszugleichen, was leider nur bedingt gelungen ist. Dennoch ist in Abb. 13 gut zu erkennen, dass
ab einer bestimmten Schichtdicke keine weitere Erhöhung der Impulsrate erfolgt; es kommt
zur Sättigung. Dies rührt augenscheinlich daher, dass β-Teilchen, die tiefer als zur Hälfte ihrer
maximalen Reichweite Rmax eingedrungen sind, die Oberfläche nicht mehr erreichen können.
Durch Mehrfachstreuung ist der effektiv zurückgelegte Weg ohnehin wesentlich größer als die
Schichtdicke, so dass in der Praxis die Sättigung schon bei etwa RS = 0, 2Rmax eintritt.
Es gibt zahlreiche empirische Formeln, die den Zusammenhang von Energie und Reichweite von
β-Strahlung beschreiben. Wir verwendeten die Formel von Weber :
0, 983
(14)
dmax = %Rmax = 5 · Eβ,max 1 −
1 + 4, 3Eβ,max
Damit konnten wir den o.g. Zusammenhang von Sättigungsschichtdicke und maximaler Reichweite verifizieren. Für dmax = 5 · dS ermittelten wir eine maximale Energie der β-Strahlung
von Eβ,max = 0, 71 MeV, während der Literaturwert 0, 672 MeV beträgt.
19
5
4
Imp/s
3
2
1
PSfrag replacements
/
0
0
0,5
1
-2
d / kg·m
Abbildung 13. Rückstreuung in Abhängigkeit von der Schichtdicke
4.4.3. Rückstreuung in Abhängigkeit von der Ordnungszahl. Hier verwendeten wir als
Rückstreumaterial Platten aus Kohlenstoff, Aluminium, Eisen, Nickel, Kupfer, Zink, Molybdän, Wismut, das Wood’sche Metall (eine Legierung aus 50% Bismut, 25% Blei, 12,5% Zinn
und 12,5% Cadmium) sowie Blei, die jeweils einige Millimeter dick waren, so dass eine Schichtdickenabhängigkeit auszuschließen ist. Die Platten wurden wie zuvor die Aluminiumfolien
über Strahler und Detektor angebracht und die Impulsrate jeweils mehrmals gemessen. Wie in
Abb. 14 zu sehen ist, steigt die Impulsrate mit steigender Ordnungszahl an. Dies ist natürlich
klar, da sich damit ja auch die Kollisionswahrscheinlichkeit erhöht. Unsere Messungen ergeben
2
den Zusammenhang Impulsrate ∼ Z 3 .
30
25
Imp/s
20
15
10
5
0
0
5
10
2/3
Z
15
20
Abbildung 14. Rückstreuung in Abhängigkeit von der Ordnungszahl
20
4.4.4. Fehlerquellen. Eine der Hauptfehlerquellen liegt in der Natur der Radioaktivität selbst.
Das Kernumwandlungen statistische Prozesse sind, können die Ergebnisse stark schwanken,
was sich ja besonders bei der Untersuchung der Schichtdickenabhängigkeit bemerkbar machte.
Hier hätten nur längere Messzeiten und eine größere Anzahl von Messungen die statistische
Sicherheit erhöhen können, wozu uns aber einfach die Zeit fehlte. Zum anderen waren alle
Rückstreumaterialien selbst radioaktiv (bei Nickel z.B. waren die Hälfte der registrierten
Impulse auf die Eigenstrahlung der Platte zurückzuführen). Wir haben diese Eigenstrahlung
zwar herausgerechnet, aber inwieweit die Ergebnisse dennoch verfälscht wurden lässt sich
schwer einschätzen. Außerdem ist die Rückstreuung auch winkelabhängig, mangels Einstellmöglichkeiten an der Apparatur können wir natürlich nicht sagen, ob wir den optimalen
Winkel zwischen Strahler, Rückstreuplatte und Detektor auch erwischt haben.
4.5. Halbwertszeit von Na - 22 (β − - Strahler).
Im Rahmen unserer Praktikumswoche war auch ein Langzeitexperiment vorgesehen. Dieses
bestand darin die Halbwertszeit von Na - 22 zu berechnen, was angesichts einer Halbwertszeit
von 2,6 Jahren (Literatur) ein ziemlich schwieriges Unterfangen war. Wir nahmen jeden Tag
10 Messwerte für die Zählrate in 10 min auf. Aus der Zählrate lässt sich die Halbwertszeit wie
folgt berechnen.
Es gilt für die Aktivität A:
(15)
A(t) = A0 e−λt ,
wobei λ die für jedes radioaktive Nuklid spezielle Zerfallskonstante ist.
Halbwertszeit bedeutet, dass nach der Zeit die Anzahl der unzerfallenden Kerne auf die Hälfte
gefallen ist.
(16)
⇒
1
A0 = A0 e−λT1/2
2
Dies führt uns zu:
(17)
T1/2 =
ln(2)
λ
Fehlt also nur noch λ. Die Zerfallskonstante bekommen wir aus Gleichung 15. Diese wird logarithmiert:
(18)
ln(A) − ln(A0 ) = −λt
Da uns nur der Anstieg der Geradengleichung interessiert, ist der Term ln(A0 ) uninteressant.
(19)
⇒
ln(A) = −λt
Folgende Mittelwerte pro Tag gab es:
Zeit in min Zählrate in 10min logarithmierte Zählrate (Zählrate in einer Minute)
0
104525.9
9.25461
1278
104350.1
9.25292
2715
104611.5
9.25542
4132
104545.5
9.25479
5452
104007.6
9.24963
21
Daraus ergibt sich folgende Grafik:
9,256
9,255
9,254
ln(A)
9,253
9,252
9,251
9,25
PSfrag replacements
↓
9,249
0
1000
2000
3000
Zeit / min
4000
5000
6000
Abbildung 15. Funktion zum Feststellen von der Zerfallskonstante λ
Die Regressionsgerade lautet:
ln(A) = −5.8329 · 10−7 t
Die Standardabweichung lautet: ∆λ = 5, 268275 · 10−7
Also ist λ = (5.8329 ± 5, 2683) · 10−7
1
.
min
1
.
min
Daraus bekommen wir mit Gleichung 17 die Halbwertszeit:
T1/2 = 1188341 ± 1315694 min ≈ 2, 3 ± 2, 5 Jahre
Im Vergleich zum Tabellenwert T1/2T abelleN a−22 = 2, 6 Jahre ist eine fast unglaubliche Übereinstimmung zu finden - der Tabellenwert liegt fast in der Mitte des Fehlertoleranzbereiches,
was ja bei einer Messzeit von fünf Tagen und einer Halbwertszeit von 2,6 Jahren nicht
selbstverständlich ist.
22
5. γ - Strahlung
5.1. Prinzip der Abschwächung von γ-Strahlen.
5.1.1. Theorie.
Die Abschwächung der γ-Strahlen beim Durchgang durch Materie beruht auf Wechselwirkung
der Gammaquanten mit dem Stoff. Diese Wechselwirkung geschieht auf drei verschiedene Arten:
• dem Fotoeffekt ,
• dem Comptoneffekt und
• der Paarbildung.
Die Schwächung lässt sich durch ein exponentielles Gesetz beschreiben, wobei der Betrag des
linearen Schwächungskoeffizienten µ dafür verantwortlich ist, wie schnell die Teilchenflussdichte
hinter dem Absorber mit zunehmender Schichtdicke abnimmt.
(20)
ϕ = ϕ0 e−µd
mit ϕ als Teilchenflussdichte hinter der Absorberschicht, ϕ0 als Teilchenflussdichte vor dem
Absorber, µ dem linearen Schwächungskoeffizienten und d der Schichtdicke des Absorbers.
Da unterschiedliche Absorbermaterialien unterschiedliche Dichte haben, ist es vorteilhaft, µ auf
die Dichte zu beziehen und so ergibt sich der Massenschwächungskoeffizient µm mit
µ
(21)
µm = ,
%
wobei % die Dichte darstellt.
Dieser Massenabschwächungskoeffizient setzt sich additiv zusammen aus dem Fotoabsorbtionskoeffizienten, dem Comptonschwächungskoeffizienten und dem Paarbildungskoeffiezienten.
Um das zu verdeutlichen, wollen wir auf die drei Wechselwirkungen kurz näher eingehen:
Fotoeffekt: Der Fotoeffekt beruht darauf, dass der γ-Quant seine gesamte Energie
Eγ = hf an ein Hüllenelektron eines Atoms des Absorbermaterials abgibt. Das Elektron wird dadurch aus der Elektronenhülle herausgeschlagen und das Photon vollständig
absorbiert. Das Atom wird dabei ionisiert.
Der Fotoeffekt ist dominierend bei niedrigen Energien des γ-Quants.
Comptoneffekt: Der Comptoneffekt kommt zustande durch inkohärente Streuung eines
Photons an einem freien Elektron (da liegt der Unterschied zum Fotoeffekt). Das γPhoton überträgt dem Elektron nach den Gesetzen des elastischen Stoßes (Energieund Impulserhaltungssatz) nur einen Teil seiner Energie und beide fliegen nach dem
Stoß in getrennten Richtungen auseinander.
Der Comptoneffekt ist dominierend bei mittleren Energien des γ-Quants.
Paarbildung: Bei der Paarbildung wandelt sich das γ-Quant im Coulombfeld des Atomkerns oder eines Hüllenelektrons in ein Elektron-Positron-Paar um und verschwindet
völlig. Nötig ist dazu mindestens eine Energie vom Betrage der doppelten Ruheenergie
eines Elektrons. Auch bei der Paarbildung gelten die Erhaltungssätze der Ladung, der
Energie und des Impulses.
Der Paarbildungseffekt ist dominierend bei hohen Energien des γ-Quants und tritt bei
unseren Experimenten nicht auf, da die von unseren Präparaten emittierten Teilchen
die doppelte Ruheenergie des Elektrons nicht erreichen.
23
5.1.2. Durchführung.
Der Versuch zur Abschwächung der γ-Strahlen mit dem Ziel der Bestimmung des Massenschwächungskoeffizienten wurde mit den radioaktiven Präparaten Cäsium Cs-137 und Kobalt
Co-60 durchgeführt. Die bei der Umwandlung von Cäsium emittierten γ-Quanten besitzen eine
kinetische Energie von 0,661 MeV, die des Cobalts im Mittel eine Energie von 1,253 MeV.
Als Absorbermaterialien wurden Blei und Aluminium verwendet. Als Detektor wurde ein Szintillationszähler verwendet.
Als erstes wurde die Detektorkennlinie aufgenommen, wobei sich gut ersichtlich in einem bestimmten Spannungsbereich ein annähernd konstantes Niveau ausbildete. In diesem Spannungsbereich wurde ein Arbeitspunkt festgelegt.
Nun wurde die Nullrate, d.h. die natürliche radioaktive Aktivität der Umgebung, bestimmt, um
sie nachher mit den Versuchsergebnissen durch Subtraktion verrechnen zu können. Die Nullrate
hatte in 60 s einen durchschnittlichen Wert von 341 Impulsen.
Am Anfang der Energieskala, also bei sehr geringen Energien tritt der Effekt des sogenannten
thermischen Rauschens auf, der die Messwerte stark verfälschen würde. Um ihn auszuschalten,
wurde am Messgerät eine Basisspannung von 3% eingestellt.
Dann wurde die Probe unter den Detektor gebracht und bei verschiedenen Absorberschichtdicken die benötigte Zeit für eine bestimmte Impulsrate am Detektor gemessen. Wir wählten
die Zeitmessung bei konstanter Impulsrate vor der Impulsmessung bei konstanter Zeit, um eine gleichbleibende Fehlergenauigkeit der Messung zu garantieren. Diese erhaltenen Zeitwerte
wurden mit einer einfachen Verhältnisgleichung in Impulse pro 60 Sekunden (Aktivität pro 60
Sekunden) umgerechnet. Das exponentielle Gesetz zur Beschreibung des Versuches lautete dann
(22)
N (d) = N (0) e−µd
mit N (d) als der Impulsrate am Detektor in Abhängigkeit der Schichtdicke, N (0) die Impulsrate ohne Absorberschicht, µ als der lineare Schwächungskoeffizient und d der Dicke der
Absorberschicht.
Zusätzlich zu den jeweils zwei Messungen mit dem Cobalt- und dem
kamen dann noch zwei Messungen mit dem Cäsiumpräparat, bei denen
im Fehlen eines vor dem Detektor angebrachten durchbohrten Bleiblocks
den 4 Messreihen vorher die Parallelität des auf den Detektor fallenden
gewährleisten sollte.
Cäsiumpräparat
der Unterschied
bestand, der in
Strahlenbündels
5.1.3. Auswertung.
Die 6 aufgenommenen Messreihen sind in Abbildung 16 dargestellt. Der Anstieg der Regressionsgeraden gibt in allen Fällen den linearen Schwächungskoeffizienten µ an. Dividiert durch
die Dichte % des Materials ergibt sich der gesuchte Massenabschwächungskoeffizient µm :
(23)
µm =
24
µ
%
ln(N(d))
ln(N(d))
ln(N(d))
5,5
5,4
5,3
5,2
5,1
5
Al ; Co
0
6,5
6,4
6,3
6,2
6,1
6
5,9
0
9,3
9,2
9,1
9
8,9
8,8
0
10
20
30
40
Al ; Cs
6
5,5
5
4,5
4
3,5
3
0
7
Pb ; Co
10
20
30
40
Pb ; Cs
6
5
4
10
20
30
40
Al ; Cs
ohne Block
10
20
30
40
Schichtdicke d in mm
50
3
0
10
9
8
7
6
5
0
10
20
30
40
Pb ; Cs
ohne Block
10
20
30
40
Schichtdicke in mm
50
Abbildung 16. Abhängigkeit Impuls (logarithmiert) und Schichtdicke
Absorber Präparat Bleiblock
µ
µm
Tab.wert für µm Abweichung in %
Al
Co
ja
-0,012 -0,0044
-0,00554
19,8
Pb
Co
ja
-0,046 -0,00404
-0,00618
34,7
Al
Cs
ja
-0,015 -0,00555
-0,00734
24,3
Pb
Cs
ja
-0,095 -0,0083
-0,0108
22,8
Al
Cs
nein
-0,0088 -0,00326
-0,00734
55,6
Pb
Cs
nein
-0,085 -0,00746
-0,0108
31,0
Aus den Ergebnissen wird ersichtlich, dass es eine systematische Abweichung in Richtung zu geringer Massenabsorbtionszahl gibt. Alle von uns bestimmten Werte liegen deutlich
unter dem zugehörigen Tabellenwert. Unsere Massenabsorbtionszahlen sind zu gering, was
bedeutet, dass die Absorbtionskurven in den Diagrammen nicht so stark abgefallen ist,
wie sie sollte. Es wurden mehr γ-Strahlen am Detektor registriert, als laut exponentieller
Gesetzmäßigkeit und Tabellenwert dort hätten ankommen dürfen. Diese Abweichung liegt bei
allen vier Experimenten in einem relativ engen Bereich von ca 20 % bis 35%. Zu begründen
ist dieser Effekt wohl damit, dass die Randbedingung für das Exponentialgesetz ein paralleler
Strahlengang ist und diese Bedingung in unserem Fall nicht gewährleistet werden kann. Aus
dem Präparat tritt ein divergentes Strahlenbündel aus. Diese Erklärung für den Fehler wird
dadurch bestätigt, dass die Abweichung bei Wegnahme des Bleiklotzes noch stärker geworden
ist. Der Klotz sorgt durch seine Bohrung für ein annähernd paralleles Bündel γ-Strahlen.
Im Falle der Aluminiumabsorbtionsschicht wurde der Fehler wesentlich schlimmer, bei der
Bleischicht nur unwesentlich. Es wurde von uns auch untersucht, ob diese systematische
Abweichung vom Tabellenwert sich erst bei großen Schichtdicken einstellt:
Absorber Präparat µm hohe Dicken µm geringe Dicken Veränderung
Al
Co
-0,0044
-0,0054
besser
Pb
Co
-0,00404
-0,00285
schlechter
Al
Cs
-0,00555
-0,00522
schlechter
Pb
Cs
-0,0083
-0,00915
besser
25
Es ist zu Erkennen, dass es jeweils zwar eine Veränderung des Wertes gibt, wenn die
hohen Schichtdicken in der Rechnung nicht berücksichtigt werden, aber keine systematische
Veränderung zum Tabellenwert oder von ihm weg. In einem Fall werden die Werte besser, im
nächsten schlechter. Unsere systematische Abweichung vom Zielwert kann darauf also nicht
zurückgeführt werden.
5.2. γ - Spektrum Cs 137.
Wir verwenden die Einkanalimpulshöhenanalyse (s. Abs. 2.1), um das Spektrum der Gammastrahlung für Caesium 137 vernünftig auswerten zu können. Für diese aufgenommene Messung
verwendeten wir eine Betriebsspannung von UB = 1000 V (s. Abb. 21), eine Kanalbreite von
2 % und eine lineare Verstärkung von 0,7. Aus der Eichung (s. Abs. 5.2.2) kann der 2 %-igen
Kanalbreite eine Energie von ca. ∆EK = 45,2 keV zugeordnet werden.
Das Cs 137 wird in einer Bleikammer in einigen cm Abstand vor den Szintillationsdetektor
positioniert. Bei konstanter Betriebsspannung erhöhen wir das 2 % bzw. ∆EK breite Kanalfenster in geeigneten Schritten. Für jede Kanalfensterposition (bestimmtes Energieintervall)
erfasst die Messapparatur über eine Messdauer von t = 20 s die Anzahl der Impulse, welche in
dem Kanalfenster liegen. Nachdem dies geschehen ist erhalten wir die in Abbildung 17 gezeigte
grafische Darstellung.
Dieses Gammaspektrum ist eine der anschaulichsten Darstellung der Wechselwirkung zwischen
Gammastrahlung und Materie. Caesium 137 emittiert bei der direkten Umwandlung in Barium
137 zu 6,9 % β − - Teilchen mit einer maximalen Energie von Emax = 1, 174 MeV. Bei 94
% aller Umwandlungen geht Cs 137 durch β − - Teilchenemission in das metastabile Bam 137
über. Dieses Bam 137, ein sog. Isomer, ist ein angeregter, metastabiler Zustand des stabilen
Ba 137 und besitzt eine Halbwertszeit von T1/2 = 2, 55 Minuten. Die vermessene Gammastrahlung entsteht durch den Übergang des Bam 137 in das stabile Ba 137. Dabei besitzen die
emittierten Gammaquanten genau eine Energie von Eγ = 0, 662 MeV. Die restliche Energie
von ERest = 0, 512 MeV wird beim Übergang Cs 137 nach Bam 137 verbraucht.
Treffen die Gammaquanten mit Eγ = 0, 662 MeV auf den Szintillator (hier NaI), so können
im wesentlichen drei Wechselwirkungen auftreten. Diese können dem Spektrum in Abb. 17
direkt entnommen werden.
Fotopeak:
Der Fotopeak entspricht der gesamten Gammaquantenenergie Eγ = 0, 662 MeV. Dieser
entsteht durch die direkte Wechselwirkung des Gammaquanten mit der Fotokathode.
Dabei verliert der Gammaquant seine gesamte Energie an der Fotokathode. Der aufmerksame Leser wird sicherlich sofort bemerken, dass das aufgenommen Spektrum bei
Eγ = 0, 662 MeV keine scharfe Linie aufweist. Aber warum? Der Theorie entsprechend
besitzen doch alle emittierten Gammaquanten des Cs 137 genau eine diskreten Energie
und somit müsste nur eine Linie bei Eγ = 0, 662 MeV im Spektrum erscheinen. Theoretisch betrachtet ist das auch so, aber praktisch leider nicht realisierbar.
Die verwendete Messapparatur besitzt ein maximale Energieauflösung. Diese wird durch
mehrere Faktoren begrenzt. Einige Faktoren wären Schwankungen des Vervielfachungsprozesses, ungleichmäßige Empfindlichkeit der Fotokathode, Ordnung des Szintillators
und statistische Schwankungen der Zahl der ausgelösten Fotoelektronen. Ein Maß für
die Energiemessgenauigkeit eines Szintillationsdetektors ist die relative Halbwertsbreite.
Bei guten Szintillationsdetektoren liegt diese unter 10 %. Der von uns verwendete Szintillationsdetektor besitzt eine relative Halbwertsbreite von ca. 9 %. Diesen akzeptable
26
600
Impulsrate
500
PSfrag replacements
Fotopeak
Rückstreuung bei 180◦
Streuung an der Messapparatur
Comptonkontinuum
Comptonkante
400
300
200
100
0
0
8
24
16
32
40
48
Pegel / %
Abbildung 17. γ - Spektrum Cs 137
Wert bekommen wir aus dem Fotopeak (s. Abb. 18) mit
(24)
HW Brel =
∆EHW B
· 100 %.
Eγ
Comptoneffekt:
Ab einer Energie von 0,2 MeV wird in dem von uns verwendeten Szintillator NaI
der Comptoneffekt (s. Abs. 5.1.1) wirksam. Dabei werden Energien von 0 bis ECEmax
(Comptonkante) registriert, je nach Streuwinkel (0◦ bis 180◦ ) und entweichender, unregistrierter Strahlung aus dem Kristall. Folgende Dinge können, abhängig vom Streuwinkel geschehen:
• Der Gammaquant streut unter Energieverlust an den Kristallatomen und löst
Comptonelektronen so heraus (Streuwinkel ϕ = 0◦ ), dass diese samt emittierter
Strahlung - durch das Auffüllen der frei gewordenen unteren Energieniveaus - auf
die Fotokathode treffen. Dieser Vorgang würde einen Impuls bei der Comptonkante
auslösen.
• Erfolgt die Streuung so, dass nur ein Teil der Comptonelektronen die Fotokathode
erreichen, so erscheint dieser Vorgang im Comptonkontinuum.
• Wird der Gammaquant um 180◦ gestreut, so wird nur ein minimaler Energiebetrag
durch die Quasireflektion frei, und erscheint als Rückstreumaximum.
Paarbildung:
Die Paarbildung (s. Abs. 5.1.1) ist in diesem Experiment leider nicht nachweisbar, da
die Gammastrahlung zu schwach ist.
Das erste Maximum, das noch vor dem Rückstreumaximum auftaucht, wird so in keinem Lehrbuch auftauchen. Dieser Peak muss durch die Messapparatur, vorrangig Bleikammer, verursacht
werden. Die einfallende Gammastrahlung muss den Szintillationskristall ohne Wechselwirkung
durchlaufen und auf die schweren Atomkerne der Bleikammer treffen. Dort verliert der Gammaquant viel Energie und wird zurück gestreut. Die Restenergie wird auf der Fotokathode
verbraten und erscheint dann als Maximum bei ca. 66,3 keV.
5.2.1. Konkrete Berechnung. Die hier angegebenen Formeln werden von uns hier nicht hergeleitet. Interessierte können die Herleitung beispielsweise im [Stolz]2 Kapitel 7 nachlesen.
2Stolz,
Werner: Radioaktivität - Grundlagen, Messung, Anwendungen“ , 3. Auflage, B.G. Teubner, 1996
”
27
Rückstreumaximum:
Für die Energie des Rückstreumaximum gilt
(25)
Eγ
ER = Eγ − ECEmax =
1 + 2 mEeγc2
= 184 keV.
0
Comptonkante:
Die Lage der Comptonkante (Streuwinkel Photon ϑ = 180◦ , Streuwinkel Comptonelektron ϕ = 0◦ ) kann mit der Formel
2 ε Eγ
= 478 keV
(26)
ECEmax =
1 + 2ε
und ε =
Eγ
me c20
berechnet werden.
5.2.2. Zur Energieeichung des γ - Spektrums. Für die Energieeichung wollten wir zuerst nur
den Fotopeak verwenden. Dies führte aber zu einer systematischen Verschiebung der restlichen
Energiebeträge im Spektrum. Deshalb benutzen wir noch den Rückstreupeak. Damit ergibt
sich folgendes Impuls-Energie Spektrum für Cs 137:
600
Streuung an der Messapparatur
Fotopeak
Rückstreuung bei 180
◦
Impulsrate
500
PSfrag replacements
Pegel / %
400
Comptonkante
300
Comptonkontinuum
200
100
0
0
200
400
600
HWB
800
Energie / keV
Abbildung 18. γ - Spektrum Cs 137 geeicht mit errechneten Energielagen
5.2.3. Differentielles und integrales Spektrum. Das oben (Abb. 17) aufgeführte differentielle
Energiespektrum des Cs 137 kann auch anders erzeugt werden. Dabei verwenden wir die Einkanalimpulshöhenanalyse mit einem Diskriminator, um ein integrales Spektrum zu erhalten.
In unserem Beispiel haben wir uns auf den Fotopeak beschränkt. Für den Pegelbereich des
Fotopeaks erhalten wir folgendes integrales Energiespektrum des Cs 137:
28
Impulsrate
1500
1000
PSfrag replacements
500
Fotopeak
Rückstreuung bei 180◦
Streuung an der Messapparatur
Comptonkontinuum
Comptonkante
Energie / keV
0
30
35
40
Pegel / %
45
50
Abbildung 19. γ - Spektrum Cs 137 integral
Differentieren wir nun dieses integrale Spektrum, so erhalten wir - unter Berücksichtigung der
Vorzeichen - den Graphen (1) in Abbildung 20. Als Vergleich haben wir noch integrale und
differentielle Messwerte dargestellt.
1500
Impulsrate
differ. Messung
integr. Messung
(1)
1000
500
PSfrag replacements
0
30
35
40
Pegel / %
45
50
Abbildung 20. γ - Spektrum Cs 137 differentiell
Offensichtlich ist es also egal, mit welcher Methode das Spektrum aufgenommen wird.
Beispielsweise kann der Abbildung 20 leicht leicht entnommen werden, dass das Maximum im
differentiellen Spektrum ein Wendepunkt im integralen Spektrum bedeutet. Beide Spektren
haben also die gleiche Aussage.
29
20000
Impulsrate
15000
10000
5000
PSfrag replacements
0
1000
500
1500
Spannung / V
Abbildung 21. Kennlinie des Szintillationsdetektors
5.3. γ - Spektrum Co 60.
Als nächstes wollen wir uns nun mit dem etwas vielfältigerem Spektrum des Co 60 beschäftigen.
Der Versuchsaufbau und die Durchführung sind analog zum Cs 137.Der Abbildung 22 entnehmen wir, dass das langlebige Kobalt (HWZ 5,272 Jahre) in mehreren Stufen in den ersten
angeregten Zustand des Ni 60 umgewandelt wird. Betrachten wir nur die Gammastrahlung, so
treten 2 Emissionen mit 2 unterschiedlichen Energien auf, Eγ1 = 1,173 Mev und Eγ2 = 1,333
MeV. Wir erwarten also eine Überlagerung von 2 γ - Spektren. Außerdem sollten wir die Paarbildung nachweisen können, da beide Energien die doppelte Ruheenergie (= 1,002 Mev) des
Elektrons überschreiten.
60
27 Co
2,821 MeV
β
−
99,85 %
PSfrag replacements
β − 0,15 %
2,506 MeV
γ1
1,333 MeV
γ2
0 MeV
60
28 Ni
Abbildung 22. Umwandlung des
30
60
27 Co
schematisch
Sehen wir uns das Spektrum an:
Impulsrate
150
100
50
PSfrag replacements
0
0
20
40
Pegel / %
60
80
Abbildung 23. γ - Spektrum Co 60
Wir wollen die einzelnen Energielagen der auftretenden Effekte mit Hilfe der in Abschnitt 5.2
genannten Formeln für die beiden Energien berechnen.
Rückstreumaximum:
ER1 =
E γ1
E
1 + 2 meγc12
= 210 keV
0
ER2 =
E γ2
E
1 + 2 meγc22
= 214 keV
0
Diese beiden Werte liegen wirklich sehr dicht nebeneinander. Deshalb erkennt man im
Spektrum nur eine von zwei Gaussverteilungen.
Comptonkante:
Auch hier gilt wieder Streuwinkel Photon ϑ = 180◦ und Streuwinkel Comptonelektron
ϕ = 0◦ .
E2
ECEmax1 =
2 meγc12
0
E γ1
me c20
1+2
= 963 keV
E2
ECEmax2 =
2 meγc22
0
1+2
E γ2
me c20
= 1116 keV
Leider liegt die zum zweiten Fotopeak gehörige Comptonkante in der Gaussverteilung
des ersten Fotopeaks. Die erste maximale Energie des Comptonelektrons ist aber deutlich zu erkennen (s. Abb. 24).
31
Paarbildung:
Je nach Absorption der γ Quanten gilt:
E11 = Eγ1 − 2me c20 = 151 keV
γ - Quant nicht absorbiert
E12 = Eγ1 − me c20 = 662 keV
ein γ - Quant absorbiert
E21 = Eγ2 − 2me c20 = 310 keV
γ - Quant nicht absorbiert
E22 = Eγ2 − me c20 = 821 keV
ein γ - Quant absorbiert
Falls beide Gammaquanten vom Szintillationszähler absorbiert werden, so erhalten wir
den Fotopeak Eγ1 oder Eγ2 , je nach Anfangsenergie des eintreffenden Gammaquants.
Die Vernichtungspeaks finden wir bei den Energien EV 1 = 511 keV und EV 2 = 1022
keV. Aus Abb. 24 wird dies aber leider nicht erkennbar. Die errechneten Peaks werden
alle durch Comptoneffekte verschluckt.
Energie in keV
160
0
200
600
800
80
ER1 und ER2
PSfrag replacements
60
40
1400
Fotopeak Eγ2
100
1200
Fotopeak Eγ1
Comptonkante ECEmax2
120
1000
Comptonkante ECEmax1
Rückstreumaxima
140
Impulsrate
400
20
0
0
5
10 15 20 25 30 35 40 45 50 55 60 65 70
Pegel / %
75 80 85 90
Abbildung 24. γ - Spektrum Co 60 geeicht
Die Energieeichung des Spektrums bekommen wir durch Newtoninterpolation der beiden Fixpunkte Eγ1 und Eγ2 .
32