PowerPoint-Präsentation - Lo

Regionaler Arbeitskreis Mathematik
Klasse 9
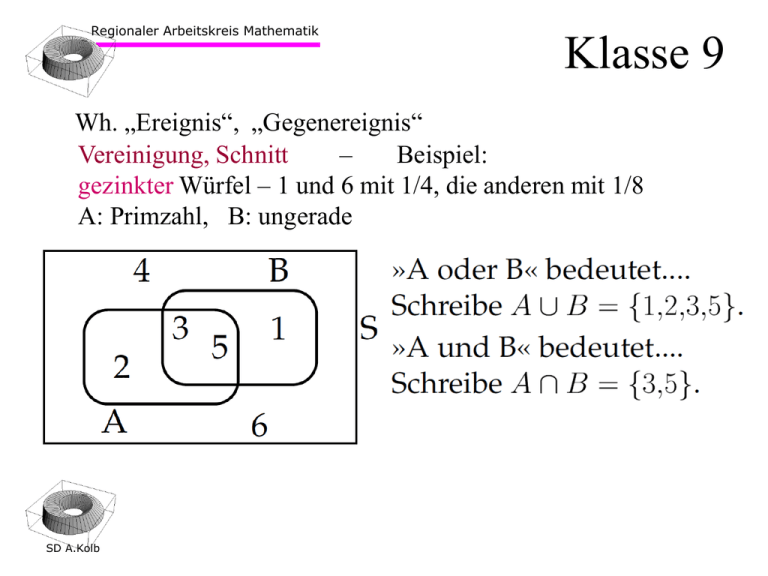
Wh. „Ereignis“, „Gegenereignis“
Vereinigung, Schnitt
–
Beispiel:
gezinkter Würfel – 1 und 6 mit 1/4, die anderen mit 1/8
A: Primzahl, B: ungerade
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse 9
Was ist also „unvereinbar“ ?
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse 9
SD A.Kolb
bedingte Wahrscheinlichkeit : Hintergrund
Regionaler Arbeitskreis Mathematik
Klasse 9
bedingte Wahrscheinlichkeit – Umsetzung
Test zum räumlichen Vorstellungsvermögen:
Vierfeldertafel
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Dasselbe mit Baumdiagrammen
SD A.Kolb
Klasse 9
Regionaler Arbeitskreis Mathematik
E: im ersten Zug Rot,
SD A.Kolb
Benutze
Klasse 9
F: im zweiten Zug Rot
zur Definition der Unabhängigkeit zweier Ereignisse
Regionaler Arbeitskreis Mathematik
Klasse 9
In der Zuverlässigkeitstheorie kann Unabhängigkeit
– z.B. bei einer Reihenschaltung von Pumpen –
vorausgesetzt werden.
P(untere Pumpe funktioniert) = 0,95
P(obere Pumpe funktioniert) = 0,95
Also: P(obere UND unter Pumpe funktionieren) =
0.950,95
Aufgabensorten: solche, bei denen Unabhängigkeit
vorausgesetzt ist und solche, bei denen Unabhängigkeit
nachgewiesen werden soll.
SD A.Kolb
Beachte Aufgabenvariationen, z.B. Wahrscheinlichkeiten
für eine der beiden Pumpen verkleinern u.Ä.
Regionaler Arbeitskreis Mathematik
Klasse10
Zufallsvariable und Erwartungswert
Eine »Zufallsvariable« ist eine Zuordnung, die jedem Ergebnis
eines Zufallsversuchs eine (reelle) Zahl zuordnet.
Beispiel: 4-mal Ziehen ohne Zurücklegen aus einer Urne:
S = {ggrr, grgr, rggr, grrg,rgrg,rrgg}
Zuordnung, genannt X, mit der
Anweisung: »Zähle, wie oft man zieht,
bis 2-mal r (also: rot) gezogen ist?
Werte xi von X :
4
3 2
P(X = 4) = 1/2, P(X = 3) = 1/3, P(X = 2) = 1/6
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Beispiel »Dreimaliger Münzwurf« (Ergebnisse: W,Z)
X: Anzahl des Auftretens von W
oder
X: Anzahl der W mal Anzahl der B
oder
X: Geldgewinn (z.B. 2€, falls WWW oder ZZZ, sonst 0€)
Beispiel: »Urne mit 4 Zetteln« (eins,sieben,hundert,tausend)
X: Anzahl der Buchstaben auf einem Zettel
x1 = 4, x2 = 6, x3 = 7 mit P(X = x1) = 1/4, P(X = x2) = 1/4,
P(X = x3) = 1/2
oder
X: Anzahl der vorkommenden »e«
x1 = 1, x2 = 2 mit P(X = x1) = 3/4 , P(X = x2) = 1/4
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Erwartungswert – Einführungsbeispiel »2-mal würfeln«
Bei 3600 Spielen etwa 8€ 200 + 4€400 = 3200€
bei 1800 Spielen etwa 8€100 + 4€200 = 1600€, die Hälfte!
bei 1 Spiel etwa (8€200 + 4€400):3600 = 8/9 € (zu erwarten)
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Einschub: die Kunst des Zählens
Klasse10
1.) Wie viele Möglichkeiten gibt es, 5 Hemden, 4 Krawatten
und und 3 Hosen zu kombinieren? 543 (Produktregel)
2.) geordnete Stichprobe mit Zurücklegen
ein Tipp beim Toto: aus der »Urne« {0,1,2} Stichprobe vom
Umfang 13, z.B. (1,1,1,0,1,1,1,2,1,1,1,0,1)
1.Stelle 3 Mögl., 2.Stelle 3 Mögl. .... also 313 mögliche
Tippreihen
Oder: wie viele 4-stellige
Nummern mit den
Ziffern aus der
Urne« {1,...,9}
 94
SD A.Kolb
»Zifferngibt es?
allg.: n in der Urne, Stichprobenumfang k  nk
Regionaler Arbeitskreis Mathematik
Klasse10
3.) geordnete Stichprobe ohne Zurücklegen
Wie viele 4-stellige Nummern mit den Ziffern aus der
»Ziffern-Urne« {1,...,9} gibt es, wenn die Ziffern sich nicht
wiederholen dürfen?  9876
allg.: n in der Urne, Stichprobenumfang k
 n(n-1)(n-2)   (n-(k-1)) =
n!
(n  k )!
Spezialfall n in der Urne, Stichprobenumfang auch n
 n(n-1)(n-2)   1 = n! Permutationen der Ziffern
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
4.) ungeordnete Stichprobe ohne Zurücklegen
n in der Urne, Stichprobenumfang k - ziehe »mit einem Griff«
Auf wie viele Arten kann man k Kugeln aus der Urne entnehmen,
wenn es nicht auf die Reihenfolge der gezogenen Kugeln
ankommt? ---- Lottoziehung!
Berechnung: Ziehe zuerst wie bei 3.) – dann muss man aber noch
durch die Permutationenanzahl k! dividieren.
Binomialkoeffizient, siehe (a+b)n
Pascalsches Dreieck
GTR: Math – PRB – 3 (=nCR)
5 nCr 3 = 10
Ende des Einschubs
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Spezielle Wahrscheinlichkeitsverteilungen  Binomialverteilung
Bernoulli-Versuch: Zufallsexperiment mit
»Treffer» oder »Niete«
»Erfolg« oder »Misserfolg«
P(Treffer) = p und folglich P(Niete) = 1-p
»Bernoulli-Kette der Länge n« - n unabhängige BernoulliVersuche nacheinander
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Beispiel: 3-mal (Laplace-)Würfeln – und es geht nur um »6«
oder »Nicht-6« !!! (Treffer und Niete)
Die Zufallsvariable X soll nun »zählen«, wie oft bei 3-mal
Würfeln »Treffer« vorkommt und die Wahrscheinlichkeit dafür
angeben. X kann die Werte 0, 1, 2 und 3 haben.
(X=3) = {(T,T,T)}
 P(X=3) = 1ppp = p3
(X=2) = {(T,T,N),(T,N,T),(N,T,T)}  P(X=2) = 3p2(1-p)
(X=1) = {(T,N,N),(N,T,N),(N,N,T)}  P(X=1) = 3p(1-p)2
(X=0) = {(N,N,N)}
 P(X=0) = 1(1-p)3
Die (grünen) Anzahlen: z.B. »auf wie viele Arten kann ich 2
T‘s auf 3 Plätze verteilen?« - das ist ungeordnet ohne
Zurücklegen, also »n über k«
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Ergebnis: die Wahrscheinlichkeitsverteilung einer binomial
verteilten Zufallsvariablen X
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Eine Münze wird 20 mal geworfen. Zu bestimmen sind die
Wahrscheinlichkeiten für die Ereignisse:
a) Genau 10 mal Wappen.
b) Höchstens 15 mal Wappen.
c) Mindestens 7 mal Wappen.
d) Mindestens 6 mal und
höchstens 16 mal Wappen.
Histogramm der
Binomialverteilung
und der kumulativen
Verteilung
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Erwartungswert einer binomialverteilten Zufallsvariablen:
betrachte die Diagramme z.B. der Verteilungen für
n = 50, p = 0,5 und n = 50, p= 0,7.
Der Erwartungswert wird unmittelbar ersichtlich als
500,5 = 25
bzw. 500,7 = 35
Also: E(X) = np
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Rechnerische Herleitung für n = 1 bzw. n = 2 und n = 3
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Praxis der Berechnungen bei der Binomialverteilung:
n = 25 und p= 0,3
P(X = 10) = 0,0916
2nd DISTR 0
P(X ≤ 6) = 0,34065
2nd DISTR A
P(X ≥ 6) = 1 – P(X ≤ 5) = ........
P(5 ≤ X ≤ 20) = P(X ≤ 20) – P(X ≤ 4)
SD A.Kolb
Regionaler Arbeitskreis Mathematik
Klasse10
Wie oft muss man einen L-Würfel mindestens werfen,
wenn man mit einer Wahrscheinlichkeit von mehr als 99%
mindestens eine 6 erhalten will?
Es geht um eine Bernoullikette der Länge n = ?,
aber p = 1/6. X zählt die vorkommenden 6er
und es muss gelten P(X ≥ 1) ≥ 0,99
also
Im Register Y=
1 – P(X = 0) ≥ 0,99
P(X = 0) ≤ 0,01
dann 2nd TABLE
Ergebnis: 26
SD A.Kolb