Document

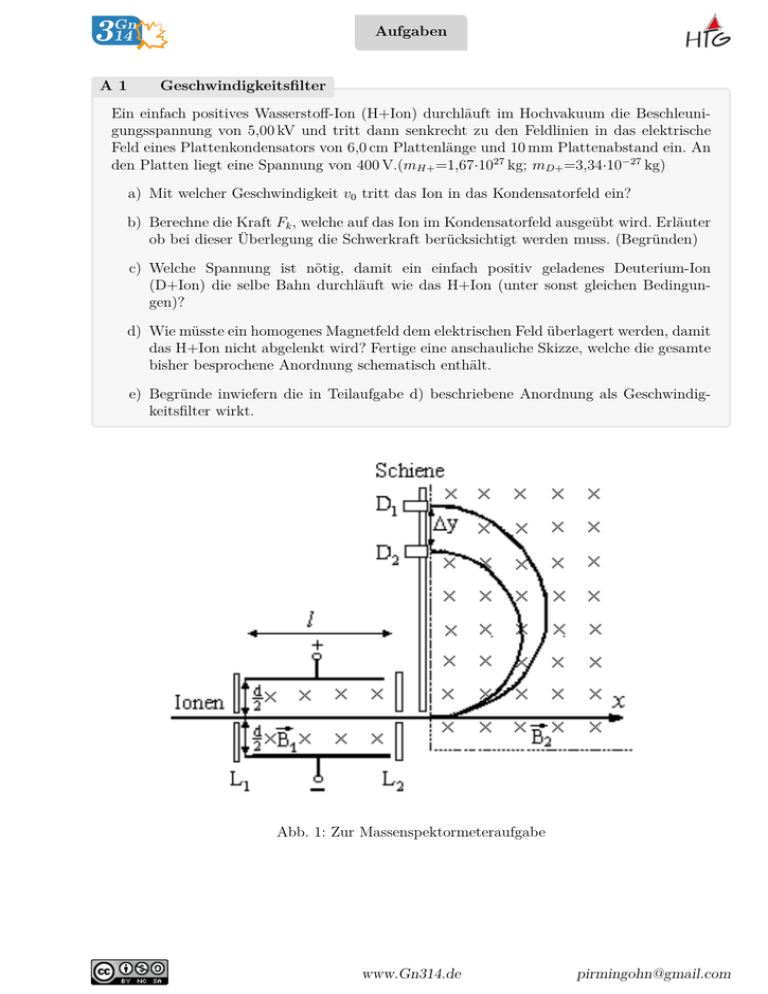
Aufgaben
A1
Geschwindigkeitsfilter
Ein einfach positives Wasserstoff-Ion (H+Ion) durchläuft im Hochvakuum die Beschleunigungsspannung von 5,00 kV und tritt dann senkrecht zu den Feldlinien in das elektrische
Feld eines Plattenkondensators von 6,0 cm Plattenlänge und 10 mm Plattenabstand ein. An
den Platten liegt eine Spannung von 400 V.(mH+ =1,67·1027 kg; mD+ =3,34·10−27 kg)
a) Mit welcher Geschwindigkeit v0 tritt das Ion in das Kondensatorfeld ein?
b) Berechne die Kraft Fk , welche auf das Ion im Kondensatorfeld ausgeübt wird. Erläuter
ob bei dieser Überlegung die Schwerkraft berücksichtigt werden muss. (Begründen)
c) Welche Spannung ist nötig, damit ein einfach positiv geladenes Deuterium-Ion
(D+Ion) die selbe Bahn durchläuft wie das H+Ion (unter sonst gleichen Bedingungen)?
d) Wie müsste ein homogenes Magnetfeld dem elektrischen Feld überlagert werden, damit
das H+Ion nicht abgelenkt wird? Fertige eine anschauliche Skizze, welche die gesamte
bisher besprochene Anordnung schematisch enthält.
e) Begründe inwiefern die in Teilaufgabe d) beschriebene Anordnung als Geschwindigkeitsfilter wirkt.
Abb. 1: Zur Massenspektormeteraufgabe
www.Gn314.de
[email protected]
A2
Massenspektrometer
Ein Gemisch aus einfach positiv geladenen Kohlenstoffionen 12 C und 14 C tritt durch eine
Lochblende L1 in einen Plattenkondensator mit dem Plattenabstand d=2,0 cm und der
Länge l=4,0 cm ein. Die gesamte Anordnung befindet sich im Vakuum. Das Magnetfeld mit
der Flussdichte B1 ist zunächst abgeschaltet; an den Platten liegt die Spannung U .
a) Skizziere die Bahnen zweier Ionen unterschiedlicher Masse, aber gleicher Geschwindigkeit zwischen L1 und L2 . Begründe welche Bahn welchem Isotop zuzuordnen ist.
(4 BE)
b) Die Ionen treten nun mit einer Mindestgeschwindigkeit 1,5 · 105 ms in den Kondensator
ein. Wie groß darf die Spannung am Kondensator höchstens sein, damit die Ionen nicht
auf die Kondensatorplatten treffen? Berechne auch die dabei maximal auftretende
Erhöhung der kinetischen Energie (in eV). (10 BE)
Am Kondensator liegt nun die Spannung U =700 V. Die Flussdichte B1 soll so eingestellt
werden, dass alle Ionen mit der Geschwindigkeit vo = 2,·105 ms den Kondensator unabgelenkt
durchqueren.
c) Berechne B1 und begründe, dass Ionen beider Kohlenstoffisotope den Kondensator
durch die Blende L2 verlassen.
Das Magnetfeld rechts von L2 hat die Flussdichte B2 = 0,14 T. Die Teilchen, die den Kondensator verlassen, durchlaufen zwei Halbkreise.
d) Zeigen, dass für den Abstand∆y der beiden Punkte, an denen die Ionen das Magnetfeld
wieder verlassen, gilt:(5 BE)
∆y =
2(mC14 − mC12 )v0
eB2
Die Flussdichte B2 wird nun variiert, alle anderen Größen bleiben unverändert. Die Ionen
sollen durch zwei verschiebbare Detektoren D1 und D2 registriert werden, die einen Mindestabstand von 1,5 cm haben. Die äußerste Position von D1 ist 60 cm von der x-Achse
entfernt.
e) Berechne, zwischen welchen Werten die Flussdichte B2 liegen muss, damit beide Isotope gleichzeitig gezählt werden können. (6 BE)
www.Gn314.de
[email protected]