T1: Theoretische Mechanik, SoSe 2016

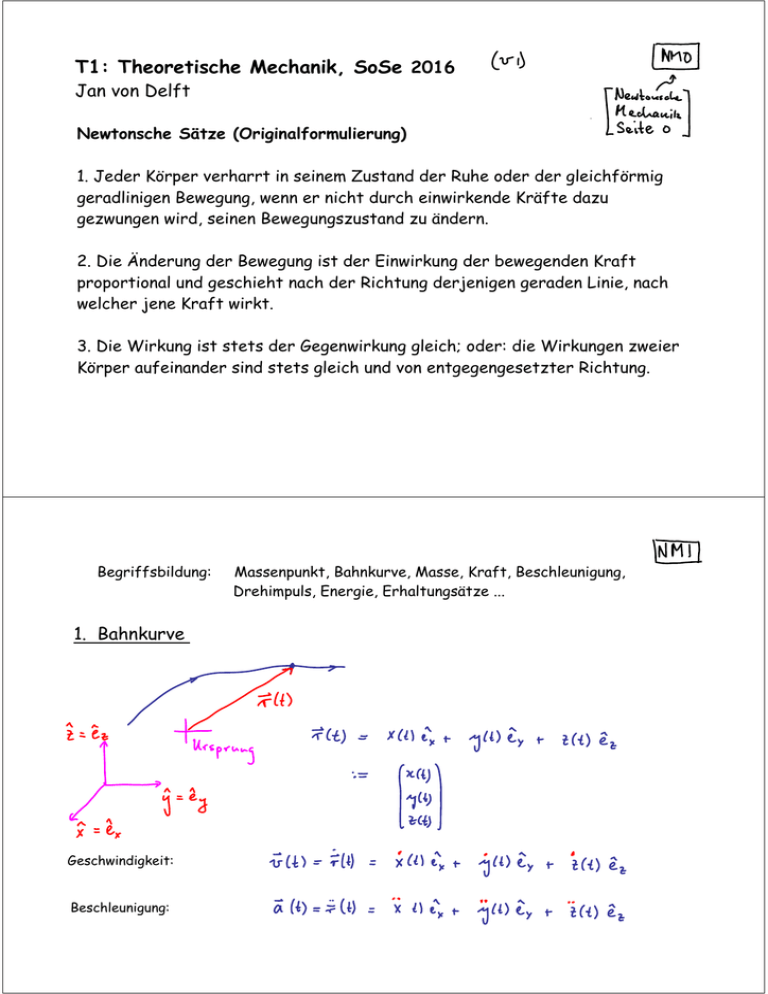
T1: Theoretische Mechanik, SoSe 2016
Jan von Delft
Newtonsche Sätze (Originalformulierung)
1. Jeder Körper verharrt in seinem Zustand der Ruhe oder der gleichförmig
geradlinigen Bewegung, wenn er nicht durch einwirkende Kräfte dazu
gezwungen wird, seinen Bewegungszustand zu ändern.
2. Die Änderung der Bewegung ist der Einwirkung der bewegenden Kraft
proportional und geschieht nach der Richtung derjenigen geraden Linie, nach
welcher jene Kraft wirkt.
3. Die Wirkung ist stets der Gegenwirkung gleich; oder: die Wirkungen zweier
Körper aufeinander sind stets gleich und von entgegengesetzter Richtung.
Begriffsbildung:
1. Bahnkurve
Geschwindigkeit:
Beschleunigung:
Massenpunkt, Bahnkurve, Masse, Kraft, Beschleunigung,
Drehimpuls, Energie, Erhaltungsätze ...
2. Newton's Axiome
Es gibt Bezugsysteme (BS), in denen kräftefreie Bewegung
durch
beschrieben wird.
1. Axiom (N1):
(Definition von
Inertialsystem)
Diese BS heißen Inertialsysteme (IS).
N1 gilt nicht in jedem BS (z.B. nicht auf Karusell).
In IS sind physikalischen Gesetze besonders einfach.
N1 ist nicht Spezialfall von N2 mit Kraft = 0, sondern
Definition von IS.
Definition:
Impuls:
Masse Geschw.
2. Axiom (N2):
(beschreibt Dynamik)
In einem IS folgt die Bewegung unter Einfluß einer
Kraft folgendem Gesetz:
Kraft
Einheit:
N2 beinhaltet
(i) Definition der Masse (vergleiche Beschl. für gleiche Kraft;,
(ii) Definition der Kraft (als Beschleunigung mal Masse);
(iii) Aussage über Bahnbewegung.
N2 gilt nur für "nicht-relativistische" Geschwindigkeiten:
3. Axiom (N3):
(Actio = Reactio)
1.ster Zusatz:
2.ter Zusatz:
(SuperpositionsPrinzip)
Kraft entlang Verbindungslinie
Gesamtkraft
Summe der Einzelkräfte
Gültigkeit von N3 ist eingeschränkt, denn N3 impliziert
"instantane" Reaktion, im Widerspruch zur speziellen
Relativitätstheorie (nichts propagiert schneller als Licht)
Ausweg: Quantenfeldtheorie: Kraft via Austausch von
Photonen f. EM-WW, Gluonen f. starke WW, Gravitonen
für Gravitation
Beispiel: Lösung von N2 für 1-dimensiones Problem
ortsabhängige Kraft
Betrachte:
wobei
Kettenregel
Integrieren:
Integrationskonstante (zeitunabhängig)
Gesamtenergie:
(erhaltene Größe,
weil zeitunabhängig)
kinetische
Potentielle
Energie
(5.5) nach
gelöst:
Vorzeichen: bestimmt Bewegungsrichtung
Trennung d. Variablen:
Anfangsbedingungen:
legen Integrationskonstante fest:
Graphische Analyse:
klassisch verbotener Bereich
Umkehrpunkte:
Bei
also bei
Zwischen Umkehrpunkten ist Bewegung periodisch:
Periode:
3. Erhaltungssätze
Zunächst mittels N2 hergeleitet, später (eleganter) mittels Lagrange-Formalismus
"zu Fuß"
"tieferer Grund": Symmetrien!
Impulserhaltung:
Falls
Definition Drehimpuls:
Definition Drehmoment:
(beide abhänging von
Wahl des Ursprungs)
N2 für Drehimpuls:
("N2 für Rotationen")
Drehimpulserhaltung:
Definition v. Arbeit:
Falls
Teilchen (Masse m) bewege sich unter Einfluss einer äusseren
Kraft von 1 nach 2 entlang Weg C12. Die von der Kraft auf m
geleistete Arbeit ist:
vom Kraftfeld auf m
übertragene Energie
Vorzeichen:
Beispiel Schwerkraft:
fallende Masse
Wenn Kraft entlang Bewegungsrichtung wirkt, leistet sie positive Arbeit.
sei eine beliebige Parametrisierung des Weges
Definition:
Kinetische Energie
Energieänderung auf Grund der
Geschwindigkeitsä d
Einheiten:
Def: Konservatives
Kraftfeld
Für ein konservatives
Kraftfeld ist die entlang
geschlossenem Weg
verreichte Arbeit
Ein Kraftfeld wird konservativ genannt, falls
die Arbeit zwischen 1 und 2 unabhängig vom Weg ist.
Theorem: Konservatives Kraftfeld
(i) ist rotationlos;
(ii) kann als Gradient eines skaleren Feldes ausgedrückt werden.
Beweis von (i):
Stokes Theorem:
(2) gilt für beliebige
Fläche, also gilt:
Beweis von (ii):
Jedes Feld der Form
erfüllt (i):
denn:
(11b.6) ausführlich:
"rotiationslos"
Vorzeichen: Konvention
skalares Feld, heißt
"Potential", oder
"potenzielle Energie"
Nullpunkt beliebig wählbar
Energieerhaltungssatz:
Integriere (11a.4)
Änderung v. U
in Richtung von
(siehe NM13)
Aber, wir wissen auch:
(- Änderung v. U)
(Änderung v.T)
Entlang einer Trajektorie (Bahn) in einem konservativem Kraftfeld bleibt die
Gesamtenergie E=T+U eines Teilchens erhalten.
Alternative
Herleitung:
Kettenregel
Energieerhaltung gilt
nicht für zeitabhängige
Potentiale:
Falls
gilt
explizite Zeitabhängigkeit,
nicht:
denn dann :
Grund: externes System ist für zeitänderung des Potentials verantwortlich,
und kann Energie zuführen oder abziehen.
Bewegungsgleichung
Erhaltungssätze
heissen "Integrale der
Bewegung", weil
sie Diff.-Gl. 1. Ordnung sind
ist eine Diff.-Gl. 2. Ordnung
ErhaltungsSätze:
Bespiel einer kons. Kraft: Lorentzkraft
Kraft auf geladenes Teilchem im Magnetfeld:
Energie ist
erhalten, also ist
Kraft konservativ.
Zusammenfassung: Newton'sche Mechanik
Def. eines Inertialsystems: Kräftefreie Bewegung:
Definitionen:
Impuls:
Drehimpuls:
Erhaltungssätze:
Definitionen:
Kinetische Energie:
Von Kraftfeld geleistete Arbeit:
Konservatives Kraftfeld:
Lorentz-Kraft:
Energieerhaltungssatz für kons. Kraft:
Drehmoment: