Seite | 17 Newtonsche Mechanik (Newton 1642

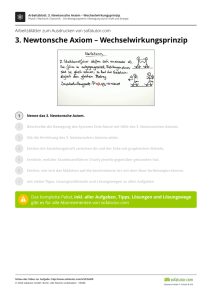
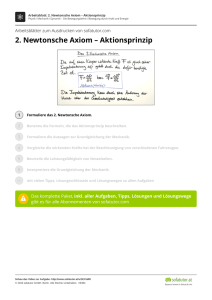
Newtonsche Mechanik (Newton 1642-­‐1727) Dynamik: untersucht Gründe einer Bewegungsänderung •
Ursachen: Kräfte -­‐
-­‐
-­‐
Kräfte sind Vektoren, 𝐹 Es gilt das Superpositionsprizip 𝐹 = 𝐹! Kräfte hängen im allgemeinen vom Ort ab 𝐹 = 𝐹 𝑟 = 𝐹(𝑥, 𝑦, 𝑧) Kraftfeld Die Newtonschen Axiome 1.Newtonsche Axiom (Trägheitsprinzip) Jeder Körper verharrt im Zustand der Ruhe oder der gleichförmigen, geradlinigen Bewegung, solange keine Kraft auf ihn wirkt. Maß für Bewegunungszustand 𝑝 = 𝑚 ∗ 𝑣 Impuls 1. Axiom: 𝑝 = 𝑐𝑜𝑛𝑠𝑡 [𝑜𝑑𝑒𝑟 𝑣 = 𝑐𝑜𝑛𝑠𝑡, 𝑜𝑑𝑒𝑟 𝑎 = 0] 2. Newtonsche Axiom (Aktionsprinzip) Ursache für eine Änderung des Bewegungszustands ist eine Kraft. Sie wird !
definiert als 𝐹⃑ = 𝑝⃑ !"
!
Für m = const folgt: 𝐹 = !" 𝑚 ∗ 𝑣 =
!"
!"
!"
𝑣 + 𝑚 !" !
𝐹 = 𝑚 ∗ 𝑎 𝐹 = 𝑘𝑔 !! = 1𝑁 (Newton) 3.Newtonsche Axiom (Reaktionsprinzip) Die Kraftwirkung zweier Körper aufeinander, sind stets gleich groß und von entgegengesetzter Richtung. (actio = reactio) 𝐹!" = −𝐹!" 𝑜𝑑𝑒𝑟 𝐹!" + 𝐹!" = 0 Seite | 17 Versuch: Luftkissenbahn m 𝐹⃑! Schwerkraft v = a * t a = Δv/Δt Aus experimentelle Ausgleichsgeraden bestimmt. a a Δt=const 1 2 Fs 1/3 ½ 1 1/m 1
𝑎~ 𝑚
𝑎~𝐹 Fs Δt 1p 2p 3p v m Δt 1 2 3 v !
ð 𝑎~ ! è 𝐹 = 𝑚 ∗ 𝑎 Def. Träge Masse Statische Messung der Kraft Verformung eines Festkörpers := elektrische Kraft zwischen Atomen Dehnung der Feder ist Maß für Kraft x-­‐x0 Δ𝑥~𝐹 X0 1 2 3 N Masse 𝐹 = −𝐷(𝑥 − 𝑥! ) m x Seite | 18 D: Federkostante F: Rückstellkraft (Def. Schwere Masse) Newtonsche Mechanik Def. Kraft !
!!! 𝐹!
Ax.I: Ruhezustand 𝐹!"# =
= 0 ‚Kräftegleichgewicht‘ z.B. F2 F1 F3 (das Kräftegleichgewicht muss in jeder Komponente x,y,z erfüllt sein!) Schwere und träge Masse Fa FD FD FG Fg = ms * g Fa = mT * a „Gewicht“ Schwere Masse 𝑎=
träge Masse 𝐹!
𝑚! ∗ 𝑔
𝑎 = 𝑔 = 𝑐𝑜𝑛𝑠𝑡
= ⇔ 𝑚! = 𝑚 ! 𝑚!
𝑚!
Seite | 19 Erhaltungssätz der Mechanik Definition: Arbeit (phys.) W: engl. Work ϕ m 𝐹⃑ 𝑠⃑ 𝐴 ≡ 𝑊 ≡ 𝐹 ∗ 𝑠 ∗ cos 𝜑 = 𝐹 ∗ 𝑠 Skalarprodukt Arbeit, die Kraft F am Teilchen der Masse m Verrichtet, wenn dieses um den Weg 𝑠 verschoben wird. s F A = 0 (𝐹 ⊥ 𝑠) Skalarprodukt = 𝑎! 𝑏! + 𝑎! 𝑏! + 𝑎! 𝑏! 𝐴⃑ 𝜗 𝐴 ∗ 𝐵 = 𝑎! 𝑒! + 𝑎! 𝑒! + 𝑎! 𝑒! ∗ 𝑏! 𝑒! + 𝑏! 𝑒! + 𝑏! 𝑒! !⃑ 𝐵
cos 𝜗 = !∗!
! !
𝑎 ∗ 𝑏 = 0 ⇔ 𝑎 ⊥ 𝑏 Wegintegral Q 𝐹⃑ (𝑟⃑) 𝑑𝑟⃑ P 𝑑𝑊 𝑟 = 𝐹(𝑟)𝑑𝑟 Skalarprodukt Seite | 20 𝑊 𝑃, 𝑄 =
!
𝐹
!
𝑟 𝑑𝑟 „Wegintegral der Kraft“ Einheit: 𝑊 = 𝐹 ∗ 𝑠 = 1𝑁 ∗ 𝑚 =
!"!!
!!
= 1𝐽 Joule (cgs-­‐System [W] = 1 dyn * cm = 1 erg (10-­‐7 J) 1eV = 1,602*10-­‐19J Im Mikrokosmos Potentielle Energie P2 (a) Wenn Wa ≡ Wb , d.h. dass das Integral wegunabhängig ist Z (b) y x P2 𝑊! − 𝑊! =
!!
𝐹𝑑𝑟!
!!
−
!!
𝐹𝑑𝑟!
!!
=
!!
𝐹𝑑𝑟!
!!
+
!!
𝐹𝑑𝑟!
!!
=
𝐹𝑑𝑟 = 0 Def-­‐: Ein Kraftfeld F(r) heisst „konservativ“ wenn das Wegintegral über die Kraft wegunbhängig ist. Für konservative Kraftfelder ist dann die folgende Größe eindeutig definiert: 𝑊=
!!
𝐹𝑑𝑟
!!
≡ 𝐸!"# 𝑃! − 𝐸!"# (𝑃! ) Δ𝐸!"# 𝑃! 𝑃! = −
!!
𝐹
!!
Def.: potentielle Energie 𝑟 𝑑𝑟 Potentielle Energiedifferenz := „negative Arbeit“ Potentielle und kinetische Energie 𝑟⃑ 2. Newtonsche Gesetz: 𝐹 = 𝑚 ∗ 𝑎 𝑜𝑑𝑒𝑟 𝑚 ∗ 𝑎 − 𝐹 = 0 m Integriere entlang des 𝐹⃑ , 𝑎⃑ 𝐹⃑ , 𝑎⃑ 𝑑𝑟 𝑑𝑟 Weges 𝑟! 𝑟 𝑟!
!!!⃑ Seite | 21 !
𝑚𝑎𝑑𝑟
!!
−
!
!!
𝑚 !" 𝑑𝑟
!!
!
𝑚𝑣𝑑𝑣
!!
!
!
!
𝐹
!!
𝑟 𝑑𝑟 = 0 + 𝐸!"# 𝑟 − 𝐸!"# 𝑟! = 0 !
= ! 𝑚 𝑣 ! 𝑟 − 𝑣 ! 𝑟!
= 𝐸!"# 𝑟! − 𝐸!"# 𝑟 !
𝑚𝑣 ! 𝑟 + 𝐸!"# 𝑟 = ! 𝑚𝑣! ² + 𝐸!"# 𝑟! = 𝑐𝑜𝑛𝑠𝑡 𝐸!"# 𝑟 + 𝐸!"# 𝑟 = 𝑐𝑜𝑛𝑠𝑡 Erhaltungssatz der klassischen Mechanik Summe von potentieller und kinetischer Energie ist an jedem Punkt 𝑟⃑ und zu jeder Zeit t erhalten. 𝐸!"# 𝑟 + 𝐸!"# 𝑟 = 𝑐𝑜𝑛𝑠𝑡 Voraussetzung: konservative Kräfte Versuche h0 Superball Federpendel Nasenpendel Seite | 22