Physik und Systemwissenschaft Test, November 2007

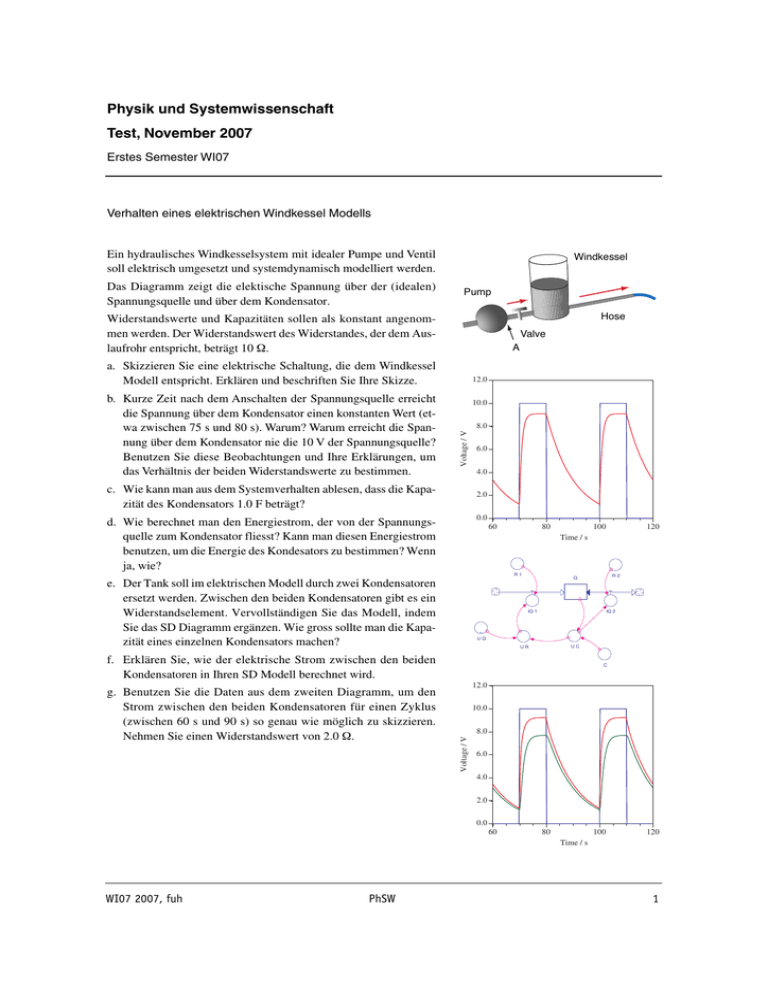
Physik und Systemwissenschaft
Test, November 2007
Erstes Semester WI07
Verhalten eines elektrischen Windkessel Modells
Ein hydraulisches Windkesselsystem mit idealer Pumpe und Ventil
soll elektrisch umgesetzt und systemdynamisch modelliert werden.
Das Diagramm zeigt die elektische Spannung über der (idealen)
Spannungsquelle und über dem Kondensator.
Windkessel
Pump
Hose
Widerstandswerte und Kapazitäten sollen als konstant angenommen werden. Der Widerstandswert des Widerstandes, der dem Auslaufrohr entspricht, beträgt 10 Ω.
Valve
A
a. Skizzieren Sie eine elektrische Schaltung, die dem Windkessel
Modell entspricht. Erklären und beschriften Sie Ihre Skizze.
10.0
8.0
Voltage / V
b. Kurze Zeit nach dem Anschalten der Spannungsquelle erreicht
die Spannung über dem Kondensator einen konstanten Wert (etwa zwischen 75 s und 80 s). Warum? Warum erreicht die Spannung über dem Kondensator nie die 10 V der Spannungsquelle?
Benutzen Sie diese Beobachtungen und Ihre Erklärungen, um
das Verhältnis der beiden Widerstandswerte zu bestimmen.
12.0
6.0
4.0
c. Wie kann man aus dem Systemverhalten ablesen, dass die Kapazität des Kondensators 1.0 F beträgt?
2.0
0.0
d. Wie berechnet man den Energiestrom, der von der Spannungsquelle zum Kondensator fliesst? Kann man diesen Energiestrom
benutzen, um die Energie des Kondesators zu bestimmen? Wenn
ja, wie?
60
80
100
R1
e. Der Tank soll im elektrischen Modell durch zwei Kondensatoren
ersetzt werden. Zwischen den beiden Kondensatoren gibt es ein
Widerstandselement. Vervollständigen Sie das Modell, indem
Sie das SD Diagramm ergänzen. Wie gross sollte man die Kapazität eines einzelnen Kondensators machen?
R2
Q
IQ 1
IQ 2
~
UQ
UC
UR
f. Erklären Sie, wie der elektrische Strom zwischen den beiden
Kondensatoren in Ihren SD Modell berechnet wird.
C
12.0
10.0
8.0
Voltage / V
g. Benutzen Sie die Daten aus dem zweiten Diagramm, um den
Strom zwischen den beiden Kondensatoren für einen Zyklus
(zwischen 60 s und 90 s) so genau wie möglich zu skizzieren.
Nehmen Sie einen Widerstandswert von 2.0 Ω.
120
Time / s
6.0
4.0
2.0
0.0
60
80
100
120
Time / s
WI07 2007, fuh
PhSW
1
12.0
10.0
Voltage / V
8.0
6.0
4.0
2.0
0.0
60
80
100
120
100
120
Time / s
12.0
10.0
Voltage / V
8.0
6.0
4.0
2.0
0.0
60
80
Time / s
WI07 2007, fuh
PhSW
2
WI07 2007, fuh
PhSW
3
~
UQ
IQ 1
UR
R1
UC
Q
C
IQ 2
R2
Solutions
Model of windkessel pump
a. Power supply, diode, two resistory, one capacitor. Voltages
across each of the elements. Two currents.
R1
UD
IQ2
UR1
Power supply models variable pressure of pump (UP). Diode
and R1 represent valve and short pipe leading into tank. Capacitor stands for tank (UC). R2 represents long pipe leading
away from tank. UD is assumed to be 0 (“ideal” diode).
UP
C
R2
UR2
UC
IQ1
b. Constant voltage UC: steady-state of capacitor because of equal
inflow and outflow: IQ1 = IQ2. Since there always is a flow IQ1,
there is a voltage UR1 which means that UC < UP.
I Q1 = I Q 2
U R1 U P − U C
U
=
IQ 2 = C
R1
R1
R2
R
UC
9.1
U − UC UC
=
⇒ 2 =
≈
= 10
⇒ P
R1
R2
R1 U P − U C 10 − 9.1
I Q1 =
Therefore, R1 should be about 1 Ω.
c. Exponential decay of UC(t) after UP has been set to zero (for example between 80 s and 100 s). The time constant is about 10 s. Since this is essentially the time constant of the system of C and R2, we have C·R2 = 10 s,
therefore C = 1 F.
d. IW_C_in = UC·IQ1. We also need the energy current out of the capacitor (IW_C_out = UC·IQ2), use the law
of balance of energy of the capacitor to obtaine dWC/dt, the integrate this rate of change (and add the result to
the initial value of the energy of the capacitor).
e. One capacitor should have half the capacitance of the previous single capacitor (therefore, C = 0.5 F per capacitor).
R1
R2
Q1
IQ 1
Q2
IQ 2
R3
IQ 3
~
2.0
UQ
UR
UC 2
UC
1.5
f. IQ2 = (UC – UC2) / R2 (R2 is the new resistor between the capacitors; R3 is the old R2!)
g. IQ2 = (UC – UC2) / R2 where R2 = 2 Ω. UC and UC2 are the
voltages shown in the graph of problem g. Their difference has
to be read from the graph and divided by 2 Ω.
WI07 2007, fuh
PhSW
Voltage / V
C
1.0
0.5
0.0
60
80
100
120
Time / s
4