Feld und Kapazität eines Plattenkondensators

Feld und Kapazität eines Plattenkondensators
r
E1
+
+
+
+
r r
E1 + E 2
r
E2
−
−
−
−
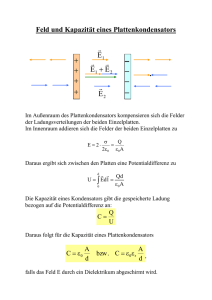
Im Außenraum des Plattenkondensators kompensieren sich die Felder
der Ladungsverteilungen der beiden Einzelplatten.
Im Innenraum addieren sich die Felder der beiden Einzelplatten zu
E = 2⋅
σ
Q
=
2ε 0 ε 0 A
Daraus ergibt sich zwischen den Platten eine Potentialdifferenz zu
r r Qd
U = ∫ Ed l =
ε0A
0
d
Die Kapazität eines Kondensators gibt die gespeicherte Ladung bezogen auf die Potentialdifferenz an:
C=
Q
U
Daraus folgt für die Kapazität eines Plattenkondensators
C = ε0
A
d
bzw. C = ε 0 ε r
A
d,
falls das Feld E durch ein Dielektrikum abgeschirmt wird.
Plattenkondensator mit Dielektrikum
Zwischen den Platten eines Kondensators gilt:
r
r
r
D = D n i = σ PL i
Das elektrische Feld ist durch das Dielektrikum zwischen den Kondensatorplatten abgeschirmt:
Dn
σ PLATTE
E = En =
=
εr ε0
εrε0
Andererseits ist das Feld E durch die Potentialdifferenz U zwischen
den Platten und die Flächenladungsdichte σ durch die Oberflächenladung Q bestimmt:
E=U
d
σ=Q
A
Damit erhält man für die Potentialdifferenz zwischen den Platten:
U=
d
Q
=Q
C
εrεo A
Misst man die Potentialdifferenz zwischen den Platten eines mit einer
definierten Ladung aufgeladenen Kondensators (Q = const. ; Ladespannung abgetrennt), so gilt:
−1
r
U∝ε
Energiespeicherung im Plattenkondensators
dW = dq ⋅ u
q
u=
C
d
r r Q
εεA
U = ∫ Ed s = = Q { 0 r }
d
C
0
Q
qdq 1 Q 2 1
=
= CU 2
W=∫
C
2 C 2
0
(Wegen C ∝ εr gilt W ∝ εr bei U = const. und W ∝ εr-1 bei Q = const)
Mit
2
ε
ε
ε
ε
εε
1
A
U
CU 2 = 0 r U 2 = 0 r 2 ( Ad ) = 0 r E 2 V
2
2 d
2 d
2
erhält man für die Energiedichte :
(unabhängig von der Geometrie des Kondensators)
1
1 rr
2
w = ε 0 ε r E = DE
2
2
Die Energie eines geladenen Kondensators steckt im elektrischen
Feld.