Grundwissen Mathe 9 - Digitale Schule Bayern

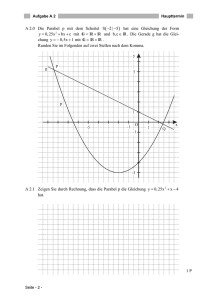
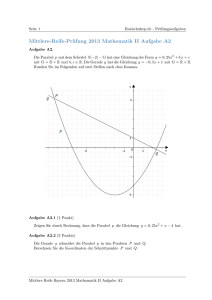
Grundwissen Mathematik
- 18 -
Otto-Hahn-Gymnasium Marktredwitz
Jahrgangsstufe 9
9.1
Reelle Zahlen
9.1.1
Menge der reellen Zahlen
Die Menge R der reellen Zahlen besteht aus der Menge
der rationalen Zahlen und der Menge der irrationalen
Zahlen, wobei die rationalen Zahlen die endlichen und
unendlichen periodischen Dezimalzahlen, die irrationalen Zahlen die unendlichen nichtperiodischen Dezimalzahlen sind.
9.1.2
Beispiele für rationale Zahlen:
5
− 6;0;− ;−0,534; 16 ;−2, 45
6
Beispiele für irrationalen Zahlen:
2 ; π ; 1,7320508...
Wurzeln
Die n-te Wurzel ( n ∈ N ) aus einer reellen Zahl a ( a ≥ 0 )
ist diejenige nichtnegative Zahl, deren n-te Potenz a
ergibt. a heißt Radikand der n-ten Wurzel.
Die zweite Wurzel aus einer reellen Zahl a ( a ≥ 0 ) heißt
Quadratwurzel. Für das Rechnen mit Quadratwurzeln
gilt:
a ⋅ b = a⋅b
a
b
=
a
b
20 ⋅ 5 = 20 ⋅ 5 = 100 = 10
( a, b ≥ 0 )
45
( a ≥ 0, b > 0 )
5
Summen und Differenzen von Quadratwurzeln kann
man nur dann zusammenfassen, wenn die Radikanden
gleich sind.
4 5 −5 3 +3 5 + 2 3 = 7 5 −3 3
Lässt sich der Radikand so faktorisieren, dass ein Faktor
eine Quadratzahl ist, kann man die Wurzel teilweise
radizieren.
Umgekehrt lässt sich ein positiver Faktor vor einer Quadratwurzel durch Quadrieren unter die Wurzel ziehen.
9.1.3
45
= 9 =3
5
=
540 = 4 ⋅ 9 ⋅ 3 ⋅ 5 = 2 ⋅ 3 ⋅ 3 ⋅ 5 = 6 15
3 5 = 3 2 ⋅ 5 = 45
Potenzen mit reellen Exponenten
Für alle reellen Zahlen a ( a ≥ 0 ) können Wurzeln auch als
Potenzen geschrieben werden:
1
1
9 = 2 9 = 92 = 3
n
a =an
n
a m = (a m ) n = a
1
m⋅
1
n
2
m
=an
( n, m ∈ N )
Die Rechengesetze für Potenzen mit rationalen Exponenten (→ Kapitel 8.1.5) gelten mit der Einschränkung
a, b ≥ 0 auch für Potenzen mit beliebigen Exponenten
( m, n ∈ R ).
6
1
27 2 = 27 6 = 27 3 = 3 27 = 3
1
(8 2 ) 6 = 8
1
1
2⋅
1
6
1
= 83 = 3 8 = 2
1
1
16 2 : 4 2 = (16 : 4) 2 = 4 2 = 4 = 2
Grundwissen Mathematik
9.2
- 19 -
Otto-Hahn-Gymnasium Marktredwitz
Zusammengesetzte Zufallsexperimente
Zufallsexperimente, bei denen mehrere Teilexperimente
nacheinander ausgeführt werden, bezeichnet man als
zusammengesetzte Zufallsexperimente oder auch als
mehrstufige Zufallsexperimente. Gut darstellbar sind
diese in Baumdiagrammen.
Pfadregel: Die Wahrscheinlichkeit eines Ergebnisses ist
gleich dem Produkt der Teilwahrscheinlichkeiten eines
Pfades.
Summenregel: Die Wahrscheinlichkeit eines Ereignisses
ist gleich der Summe der Wahrscheinlichkeiten der
Ergebnisse, die zu diesem Ereignis gehören.
9.3
Quadratische Funktionen
9.3.1
Allgemeiner Funktionsterm
f ( x) = ax 2 + bx + c
Bsp.: Urne mit 2 schwarzen und 3 weißen Kugeln.
Zwei Mal hintereinander Ziehen ohne Zurücklegen.
S
2
5
3
5
W
1
4
S
2 1
1
⋅ =
5 4 10
3
4
W
2 3
3
⋅ =
5 4 10
2
1
=
4
2
S
3 1
3
⋅ =
5 2 10
W
3 1
3
⋅ =
5 2 10
2
1
=
4
2
mit a, b, c ∈ R; a ≠ 0
Der Graph einer quadratischen Funktion heißt Parabel.
f ( x) = x 2 ist der Funktionsterm der Normalparabel.
9.3.2
Öffnungsverhalten
a positiv:
die Parabel ist nach oben geöffnet
der Scheitel ist der tiefste Punkt der Parabel.
a negativ: die Parabel ist nach unten geöffnet
der Scheitel ist der höchste Punkt der Parabel.
| a |= 1 :
die Parabel hat die Form der Normalparabel.
| a |> 1 :
die Parabel ist enger als die Normalparabel.
| a |< 1 :
die Parabel ist weiter als die Normalparabel.
9.3.3
Scheitelform
Parabelgleichung: y = ax 2 + bx + c mit a, b, c ∈ R; a ≠ 0
y = −2 x 2 − 12 x − 17
Scheitelform: y = a( x 2 − d ) + e
y = −2 ⋅ ( x 2 + 6) − 17
mit a, d , e ∈ R; a ≠ 0
Mittels
quadratischer
Ergänzung
kann
die
Parabelgleichung in die Scheitelform überführt
werden, aus der man die Koordinaten des Scheitels
S (d | e) ablesen kann.
9.3.4
Nullstellen
Eine Parabel kann zwei, einen oder keinen Schnittpunkt
mit der x-Achse haben. Diese Schnittpunkte mit der
x-Achse
entsprechen
den
Nullstellen
der
2
quadratischen Funktion f ( x) = ax + bx + c und sind
die Nullstellen der Gleichung y = ax 2 + bx + c .
Zur Berechnung der Nullstellen einer Parabel löst man
die Gleichung ax 2 + bx + c = 0 (→ Kapitel 9.4)
y = −2 ⋅ ( x 2 + 6 + 9 − 9) − 17
y = −2 ⋅ (( x + 3) 2 − 9) − 17
y = −2 ⋅ ( x + 3) 2 + 1
⇒ S (−3 / 1)
Grundwissen Mathematik
9.4
- 20 -
Otto-Hahn-Gymnasium Marktredwitz
Quadratische Gleichungen
Zum Lösen einer quadratischen Gleichung der Form
ax 2 + bx + c = 0 dient die Lösungsformel (auch
Mitternachtsformel oder Mondscheinformel).
x1/ 2 =
− x 2 + 6x − 8 = 0
x1 / 2 =
− 6 ± 6 2 − 4 ⋅ (−1) ⋅ (−8)
2 ⋅ (−1)
⇒ x1 = 2, x 2 = −4 ( D = 4)
− b ± b 2 − 4ac
2a
=
−6±2
−2
x 2 + 4x + 4 = 0
D = b 2 − 4ac heißt Diskriminante
− 4 ± 4 2 − 4 ⋅1 ⋅ 4 − 4 ± 0
=
2 ⋅1
2
⇒ x1 = −2 ( D = 0)
x1 / 2 =
D > 0 : die Gleichung hat 2 Lösungen
eine zugehörige Parabel hat 2 Nullstellen
D = 0 : die Gleichung hat eine Lösung
eine zugehörige Parabel hat eine Nullstelle
D < 0 : die Gleichung hat keine Lösung
eine zugehörige Parabel hat keine Nullstellen
9.5
Die Satzgruppe des Pythagoras
9.5.1
Satz des Pythagoras
3x 2 − 10 x + 25 = 0
D = (−10) 2 − 4 ⋅ 3 ⋅ 25 = −200 < 0
⇒ keine Lösung
In jedem rechtwinkligen Dreieck hat das Quadrat über der
Hypotenuse den gleichen Flächeninhalt wie die
Summe der Kathetenquadrate.
Formel: a 2 + b 2 = c 2
b²
c²
Kathetensatz
b²
Im rechtwinkligen Dreieck ist das Quadrat einer
Kathetenlänge gleich dem Produkt aus der
Hypotenusenlänge und der Länge des anliegenden
Hypotenusenabschnitts.
Formel: a 2 = c ⋅ p
bzw.
b2 = c⋅q
b
cp
Höhensatz
h
rechtwinkligen Dreieck ist das Quadrat der
Hypotenusenhöhe gleich dem Produkt aus den Längen
der beiden Hypotenusenabschnitte.
Formel: h 2 = p ⋅ q
sin α =
cos α =
tan α =
p
c
Im
9.5.4
a
q
c
9.5.3
a
c
Kehrsatz zum Satz des Pythagoras
Wenn in einem Dreieck ABC a 2 + b 2 = c 2 gilt, dann hat
das Dreieck bei C einen rechten Winkel.
9.5.2
a²
b
b
h
q
p q
h2
c p p
Trigonometrische Beziehungen im rechtwinkligen Dreieck
sin 2 α + cos 2 α = 1
Gegenkathete
Hypotenuse
Ankathete
Hypotenuse
Gegenkathete sin α
=
Ankathete
cos α
(Trigonometrischer Pythagoras)
Ankathete zu α
α
Hypotenuse
Gegenkathete
zu α
sin α = cos(90° − α )
cos α = sin(90° − α )
(Komplementwinkelbeziehungen)
Grundwissen Mathematik
9.5.5
- 21 -
Otto-Hahn-Gymnasium Marktredwitz
Anwendung auf ebene und räumliche Figuren
Quadrat
Rechteck
d
d
s
s
gleichschenkliges Dreieck
a
h
hc
c
l
d = l 2 + b2
d =s 2
a
a
a
b
gleichseitiges Dreieck
hc = a 2 −
Würfel
a
1 2
c
4
h=
Quader
Tetraeder
s
s
h
d
1
3a
2
d
h
s
b
l
s
d = l 2 + b2 + h2
d =s 3
9.6
s
1
h=
6 ⋅s
3
Oberflächeninhalt und Volumen verschiedener Körper
G ist die Grundfläche, M die Mantelfläche und h die Höhe des jeweiligen Körpers
Prisma
O = 2⋅G + M
Zylinder
Pyramide
Kegel
O = 2⋅G + M
O=G+M
O=G+M
2
V = G⋅h
G=r π
G = r 2π
M = 2πr ⋅ h
M = πrs mit s = h 2 + r 2
1
V = ⋅G ⋅h
3
V=
V = G⋅h
1
⋅G ⋅h
3
s
s
h
h
h
x
r
ha
h
α
a
β
a
s
.
r
α