Übungsaufgabe zu Quadratischen Funktionen

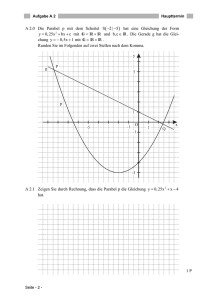
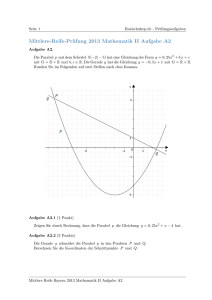
Übungsaufgabe zu Quadratischen Funktionen
1.
Gegeben ist die Parabel p mit dem Scheitel S (6 | 10), die durch den Punkt
T(8 | 9) verläuft. (G= IRxIR)
1.1
Berechnen Sie die Gleichung der Parabel p in allgemeiner Form und geben Sie die
Gleichung der Symmetrieachse und die Wertemenge an.
[Teilergebnis: p: y= -0,25x² + 3x + 1
1.2
Erstellen Sie für p eine Wertetabelle für x  [-1 ; 12] mit x = 1 und zeichnen
Sie die Parabel p in ein Koordinatensystem.
[Für die Zeichnung: Längeneinheit 1 cm; -1 < x < 12; -4 < y < 10]
1.3
Die Gerade g hat die Gleichung g: y = 2x + 2.
Zeichnen Sie g in das Koordinatensystem mit ein.
Weisen Sie rechnerisch nach, dass g eine Tangente an p ist und bestimmen Sie die
Koordinaten des Berührpunktes Q.
1.4
Die Punkte Cn(x | -0,25x² + 3x + 1) liegen auf der Parabel p.
Die Punkte Bn liegen ebenfalls auf p, wobei die Abszisse der Punkte Bn jeweils um 4
größer ist als die Abszisse x der Punkte Cn.
Sie bilden für x  lR, zusammen mit dem Punkt A(4 | 1) Eckpunkte von Dreiecken
ABnCn.
Zeichnen Sie das Dreieck AB1C1 für x = 7 und das Dreieck AB2C2 für x = -0,5 in das
Koordinatensystem mit ein.
1.5
Zeigen Sie, dass für die Koordinaten der Punkte Bn in Abhängigkeit der Abszisse x
der Punkte Cn gilt: Bn (x+4 | - 0,25 x² + x + 9)
1.6
Stellen Sie den Flächeninhalt A(x) der Dreiecke ABnCn in Abhängigkeit von x dar.
[Ergebnis: A(x)=(0,5x² - 2x + 16) FE]
1.7
Das Dreieck AB0C0 hat den kleinsten Flächeninhalt aller Dreiecke ABnCn.
Ermitteln Sie Amin und den zugehörigen Wert für x.
Berechnen Sie die Koordinaten von B0 und C0 .
1.8
Es gibt Dreiecke, bei denen die Seite [AC] parallel zur Geraden g ist.
Für welche x-Werte gilt das? Wählen Sie davon das Dreieck AB3C3 aus, das einen
positiven x-Wert hat.
[Teilergebnis: x = 8]
Um wieviel Prozent ist der Flächeninhalt des Dreiecks AB3C3 größer als Amin ?