9.Klasse - Gymnasium Schrobenhausen

Gymsob
1
Grundwissen Mathematik 9.Klasse
Gymnasium SOB
1.Weiterentwicklung der Zahlvorstellung
•
Definition der Quadratwurzel: Für a ≥ 0 ist a diejenige nicht negative Zahl deren
Quadrat a ergibt. a heißt Quadratwurzel, a heißt Radikand.
•
•
64 = 8
Beispiele: 0,25 = 0,5
Reelle Zahlen stellen eine Erweiterung der
rationalen Zahlen dar. Diese ist nötig, da
z.B. 2 nicht in Q liegt. Jeder
unendliche nichtperiodische
Dezimalbruch ist irrational, es gibt
keine Bruchdarstellung für ihn, π ist
irrational. Die reellen Zahlen R
umfassen die rationalen und die
irrationalen Zahlen.
•
a 2 = a für a ≥ 0
•
a 2 = − a für a < 0
•
a ⋅ b=
a⋅b
•
a : b=
a:b
•
Achtung!
a +
b≠
a+ b
9 +
R
16 = 7 ≠ 5 =
Q
Z
25
2.Funktionale Zusammenhänge
2.1.Graphen quadratischer Funktionen und ihre Nullstellen
•
•
•
•
•
•
•
•
•
•
•
1.Binomische Formel: a² + 2ab + b² = (a + b)²
2.Binomische Formel: a² - 2ab + b² = (a - b)²
3.Binomische Formel: a² - b² = (a - b)(a + b)
Der Graph einer quadratischen Funktion
f(x) = ax² + bx + c mit a ≠ 0 heißt Parabel.
Beispiel: Graph für f(x) = 0,5x² + 2x – 1
Der tiefste bzw. höchste Punkt einer Parabel
wird Scheitel S genannt.
Die Stellen an denen der Graph die x – Achse
schneidet heißen Nullstellen.
Falls a > 0 ist die Parabel nach oben geöffnet.
Falls a < 0 ist die Parabel nach unten
geöffnet.
Falls |a| > 1 ist, erhält man eine engere Parabel.
Falls |a| < 1 ist, erhält man eine weitere Parabel.
N
Gymsob
2
2.2.Lösungsverfahren für quadratische Gleichungen
•
•
•
•
•
Eine Gleichung der Form ax² + bx + c = 0 heißt quadratische Gleichung.
Durch quadratische Ergänzung kann man sie auf Scheitelpunktform bringen und
lösen.
Beispiel:
0,75x² + 4,5x + 3 = 0
| 0,75 ausklammern
0,75 [x² + 6x + 4] = 0
| quadratisch ergänzen
0,75 [x² + 6x + 3² - 3² + 4] = 0
| binomische Formel
0,75 [(x + 3)² - 5] = 0
| ausmultiplizieren liefert die
Scheitelpunktform
0,75 (x + 3)² - 3,75= 0
| Auflösen nach x
(x + 3)² = 3,75: 0,75
(x + 3)² = 5
x1 = 5 − 3 x 2 = − 5 − 3
Aus der Scheitelpunktform f(x) = a(x – d)² + e lassen sich der Scheitel S(d/e), die
Verschiebung der Parabel in x – Richtung um d und die Verschiebung in y – Richtung
um e direkt ablesen.
Die Bestimmung der Nullstellen kann neben der quadratischen Ergänzung mit der
Lösungsformel erfolgen:
•
x1 =
− b±
2
b ² − 4ac
2a
Der Radikand in der Lösungsformel wird Determinante D genannt und gibt die Anzahl
der Lösungen an. Für D > 0 gibt es zwei Lösungen, für D = 0 eine Lösung und für
D < 0 keine Lösung.
2.3.Anwendungen
•
•
•
Extremwertprobleme
Schnittpunktbestimmung von zwei Parabeln, Parabel und Gerade und Gerade und
Hyperbel.
Einfache Bruchgleichungen
3.Erweiterung des Potenzbegriffs
3.1.n – te Wurzeln
•
•
Für a ≥ 0 ist
a diejenige nicht negative Zahl, deren n – te Potenz a ergibt:
n
.
a heißt n- te Wurzel aus a (n ∈ N, n≥ 2)
3
Beispiele:
27 = 3
x³ = -8  x = − 3 8 = − 2
x4 = 16  x1 = 2 und x2 = -2
n
( a)
n
3.1.Potenzen mit rationalen Exponenten
n
a= a
1
n
a
p
q
•
Definition: Für positive Basen gilt:
•
Rechenregeln für r und s aus Q und a und b aus R+:
a r ⋅ a s = a r+ s
a r : a s = a r− s
(a )
r s
= a r⋅ s
=
q
ap
a r ⋅ b r = ( ab )
r
a
− p
q
=
1
q
ap
a r : b r = ( a : b)
r
n
= a
Gymsob
3
4.Zusammengesetzte Zufallsexperimente
•
•
•
•
Ein Zufallsexperiment, das aus mehreren
5
3
Teilexperimenten besteht, nennt man
8
8
mehrstufiges Zufallsexperiment.
Beispiel: In einer Urne sind 5 gelbe und
3 blaue
3 5
Kugeln. Es werden
2
4
nacheinander ohne
7 7
Zurücklegen 2 Kugeln
7
7
gezogen.
1.Pfadregel: Bei einem
mehrstufigen
Zufallsexperiment erhält man die Wahrscheinlichkeit eines Ergebnisses, indem man
die Wahrscheinlichkeiten längs des zugehörigen Pfades im Baumdiagramm
5 3
multipliziert: P(g,b) = ⋅ .
8 7
2.Pfadregel: Bei einem mehrstufigen Zufallsexperiment erhält man die
Wahrscheinlichkeit eines Ereignisses, indem man die Summe der
Wahrscheinlichkeiten der Pfade bildet, die zu dem Ereignis gehören:
5 3 3 2
P({(g,b),(b,b)}) = ⋅ + ⋅ .
8 7 8 7
5.Das rechtwinklige Dreieck
5.1.Satzgruppe des Pythagoras
•
Kathetensatz: Für jedes rechtwinklige Dreieck ist das
Quadrat übereiner Kathete flächengleich zum Rechteck
aus der Hypotenuse und dem anliegenden
Hypotenusenabschnitt. a² = c · p
b² = c · q Die
Hypotenuse ist die dem rechten Winkel
gegenüberliegende Seite. Die Katheten sind die anderen
beiden Seiten. Die Höhe der Hypotenuse zerlegt diese in
die Hypotenusenabschnitte.
•
Satz des Pythagoras: In jedem
rechtwinkligen Dreieck haben die Quadrate
über den Katheten den gleichen
Flächeninhalt wie das Quadrat über der
Hypotenuse. a² + b² = c²
Kehrsatz zum Satz des Pytagoras: Wenn in
einem Dreieck a² + b² = c² gilt, dann hat das
Dreieck bei C einen rechten Winkel.
Diagonale d im Quadrat mit der Seitenlänge
d = 2a
Höhe im gleichseitigen Dreieck mit der
a
Seitenlänge a: h = 3
2
•
•
•
a:
Gymsob
•
4
Höhensatz: In jedem rechtwinkligen Dreieck
ist das Quadrat über der Höhe flächengleich
zum Rechteck aus den beiden
Hypotenusenabschnitten. h² = p · q
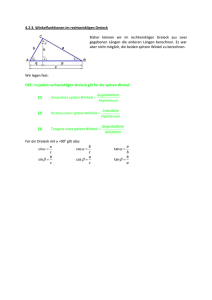
5.2.Trigonometrie am rechtwinkligen
Dreieck
•
•
•
Gegenkathete von α
=
Hypotenuse
Ankathete von α
b
cos α =
=
Hypotenuse
c
Gegenkathete von α
tan α =
=
Ankathete von α
sin α =
•
sin α = cos(90° − α );
•
Besondere Werte:
0°
sin 0
a
c
a
b
cos α = sin(90° − α );
30°
1 1= 1
2
2
cos 1 4 = 1 1 3
2
2
tan 0
1
3
45°
1 2
2
1 2
2
1
tan α =
sin α
;
cos α
60°
1 3
2
1 1= 1
2
2
3
sin 2 α + cos 2 α = 1
90°
1 4=1
2
0
n.d.
Gymsob
5
6.Raumgeometrie
6.1. Prisma und Zylinder
•
Höhe h
G
Netz des Prismas:
h
πr²
•
Netz des Zylinders:
Höhe h
M
Mantelfläche M
G
M = 2πrh
πr²
•
Oberfläche und Volumen des Prismas:
•
Oberfläche und Volumen des Zylinders:
OP = 2 · G + M
VP = G · h
OZ = 2 · G + M = 2πr² + 2πr·h
VZ = G · h = πr²·h
6.2. Pyramide und Kegel
•
Netz des Kegels und der Pyramide:
b=2πr
S
M=πrs
s
πr²
s
•
Oberfläche und Volumen der Pyramide:
OP = Grundfläche + Seitenflächen
VP = 1/3 G · h
•
Oberfläche und Volumen des Kegels:
OK = πr² + πrs
VK = 1/3 G · h = 1/3 πr² · h